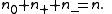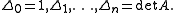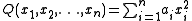Sylvester's law of inertia
Encyclopedia
Sylvester's law of inertia is a theorem
in matrix algebra
about certain properties of the coefficient
matrix
of a real
quadratic form
that remain invariant
under a change of coordinates. Namely, if A is the symmetric matrix that defines the quadratic form, and S is any invertible matrix such that D = SAST is diagonal, then the number of negative elements in the diagonal of D is always the same, for all such S; and the same goes for the number of positive elements.
This property is named after J. J. Sylvester who published its proof in 1852.
entries. Any non-singular matrix S of the same size is said to transform A into another symmetric matrix B = SAST, also of order n, where ST is the transpose of S. If A is the coefficient matrix of some quadratic form of Rn, then B is the matrix for the same form after the change of coordinates defined by S.
A symmetric matrix A can always be transformed in this way into a diagonal matrix D which has only entries 0, +1 and −1 along the diagonal. Sylvester's law of inertia states that the number of diagonal entries of each kind is an invariant of A, i.e. it does not depend on the matrix S used.
The number of +1s, denoted n+, is called the positive index of inertia of A, and the number of −1s, denoted n−, is called the negative index of inertia. The number of 0s, denoted n0, is the dimension of the kernel of A, and also the corank of A. These numbers satisfy an obvious relation
The difference sign(A) = n− − n+) is usually called the signature of A. (However, some authors use that term for the whole triple (n0, n+, n−) consisting of the corank and the positive and negative indices of inertia of A.)
If the matrix A has the property that every principal upper left k×k minor Δk is non-zero then the negative index of inertia is equal to the number of sign changes in the sequence
s, a real quadratic form Q in n variables (or on an n-dimensional real vector space) can by a suitable change of basis be brought to the diagonal form
with each ai ∈ {0, 1, −1}. Sylvester's law of inertia states that the number of coefficients of a given sign is an invariant of Q, i.e. does not depend on a particular choice of diagonalizing basis. Expressed geometrically, the law of inertia says that all maximal subspaces on which the restriction of the quadratic form is positive definite
(respectively, negative definite) have the same dimension. These dimensions are the positive and negative indices of inertia.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in matrix algebra
Matrix algebra
Matrix algebra may refer to:*Matrix theory, is the branch of mathematics that studies matrices*Matrix ring, thought of as an algebra over a field or a commutative ring...
about certain properties of the coefficient
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of an expression ; it is usually a number, but in any case does not involve any variables of the expression...
matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
of a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
quadratic form
Quadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
that remain invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
under a change of coordinates. Namely, if A is the symmetric matrix that defines the quadratic form, and S is any invertible matrix such that D = SAST is diagonal, then the number of negative elements in the diagonal of D is always the same, for all such S; and the same goes for the number of positive elements.
This property is named after J. J. Sylvester who published its proof in 1852.
Statement of the theorem
Let A be a symmetric square matrix of order n with realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
entries. Any non-singular matrix S of the same size is said to transform A into another symmetric matrix B = SAST, also of order n, where ST is the transpose of S. If A is the coefficient matrix of some quadratic form of Rn, then B is the matrix for the same form after the change of coordinates defined by S.
A symmetric matrix A can always be transformed in this way into a diagonal matrix D which has only entries 0, +1 and −1 along the diagonal. Sylvester's law of inertia states that the number of diagonal entries of each kind is an invariant of A, i.e. it does not depend on the matrix S used.
The number of +1s, denoted n+, is called the positive index of inertia of A, and the number of −1s, denoted n−, is called the negative index of inertia. The number of 0s, denoted n0, is the dimension of the kernel of A, and also the corank of A. These numbers satisfy an obvious relation
The difference sign(A) = n− − n+) is usually called the signature of A. (However, some authors use that term for the whole triple (n0, n+, n−) consisting of the corank and the positive and negative indices of inertia of A.)
If the matrix A has the property that every principal upper left k×k minor Δk is non-zero then the negative index of inertia is equal to the number of sign changes in the sequence
Statement in terms of eigenvalues
The positive and negative indices of a symmetric matrix A are also the number of positive and negative eigenvalues of A. Any symmetric real matrix A has an eigendecomposition of the form QEQT where E is a diagonal matrix containing the eigenvalues of A, and Q is an orthonormal square matrix containing the eigenvectors. The matrix E can be written E = WDWT where D is diagonal with entries 0, +1, or −1, and W is diagonal with Wii = √|Eii|. The matrix S = QW transforms D to A.Law of inertia for quadratic forms
In the context of quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
s, a real quadratic form Q in n variables (or on an n-dimensional real vector space) can by a suitable change of basis be brought to the diagonal form
with each ai ∈ {0, 1, −1}. Sylvester's law of inertia states that the number of coefficients of a given sign is an invariant of Q, i.e. does not depend on a particular choice of diagonalizing basis. Expressed geometrically, the law of inertia says that all maximal subspaces on which the restriction of the quadratic form is positive definite
Definite bilinear form
In mathematics, a definite bilinear form is a bilinear form B over some vector space V such that the associated quadratic formQ=B \,...
(respectively, negative definite) have the same dimension. These dimensions are the positive and negative indices of inertia.
External links
- Sylvester's law on PlanetMathPlanetMathPlanetMath is a free, collaborative, online mathematics encyclopedia. The emphasis is on rigour, openness, pedagogy, real-time content, interlinked content, and also community of about 24,000 people with various maths interests. Intended to be comprehensive, the project is hosted by the Digital...
.