Supporting functional
Encyclopedia
In convex analysis
and mathematical optimization, the supporting functional is a generalization of the supporting hyperplane
of a set.
, and
be a convex set
, then the continuous linear functional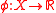
is a supporting functional of C at the point 
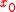if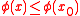 
for every 
.
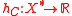(where 
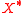is the dual space
of
) is a support function of the set C, then if 
, it follows that 
defines a supporting functional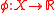 
of C at the point 
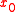such that 
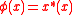for any 
.
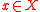is a supporting functional of the convex set C at the point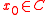 
such that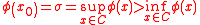
then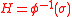
defines a supporting hyperplane to C at 
.
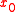Convex analysis
Convex analysis is the branch of mathematics devoted to the study of properties of convex functions and convex sets, often with applications in convex minimization, a subdomain of optimization theory....
and mathematical optimization, the supporting functional is a generalization of the supporting hyperplane
Supporting hyperplane
Supporting hyperplane is a concept in geometry. A hyperplane divides a space into two half-spaces. A hyperplane is said to support a set S in Euclidean space \mathbb R^n if it meets both of the following:...
of a set.
Mathematical definition
Let X be a locally convex topological spaceTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, and
be a convex setConvex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
, then the continuous linear functional
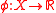is a supporting functional of C at the point 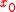if 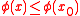for every .Relation to support function
If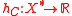 (where 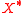is the dual spaceDual space
In mathematics, any vector space, V, has a corresponding dual vector space consisting of all linear functionals on V. Dual vector spaces defined on finite-dimensional vector spaces can be used for defining tensors which are studied in tensor algebra...
of
) is a support function of the set C, then if , it follows that defines a supporting functional 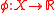of C at the point 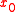such that 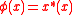for any 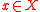.Relation to supporting hyperplane
If is a supporting functional of the convex set C at the point 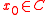such that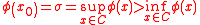then
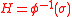defines a supporting hyperplane to C at .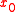