
Superperfect number
Encyclopedia
In mathematics a superperfect number is a positive integer
n that satisfies
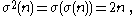
where σ is the divisor function
. Superperfect numbers are a generalization of perfect number
s.
The first few superperfect numbers are
If n is an even superperfect number then n must be a power of 2, 2k, such that 2k+1-1 is a Mersenne prime
.
It is not known whether there are any odd superperfect numbers. An odd superperfect number n would have to be a square number such that either n or σ(n) is divisible by at least three distinct primes. There are no odd superperfect numbers below 7x1024.
Perfect and superperfect numbers are examples of the wider class of (m,k)-perfect numbers which satisfy

With this notation, perfect numbers are (1,2)-perfect and superperfect numbers are (2,2)-perfect. Other classes of (m,k)-perfect numbers are:
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
n that satisfies
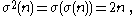
where σ is the divisor function
Divisor function
In mathematics, and specifically in number theory, a divisor function is an arithmetical function related to the divisors of an integer. When referred to as the divisor function, it counts the number of divisors of an integer. It appears in a number of remarkable identities, including relationships...
. Superperfect numbers are a generalization of perfect number
Perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its proper positive divisors, that is, the sum of its positive divisors excluding the number itself . Equivalently, a perfect number is a number that is half the sum of all of its positive divisors i.e...
s.
The first few superperfect numbers are
- 2, 4, 1616 (number)16 is the natural number following 15 and preceding 17. 16 is a composite number, and a square number, being 42 = 4 × 4. It is the smallest number with exactly five divisors, its proper divisors being , , and ....
, 6464 (number)64 is the natural number following 63 and preceding 65.-In mathematics:Sixty-four is the square of 8, the cube of 4, and the sixth power of 2. It is the smallest number with exactly seven divisors. It is the lowest positive power of two that is adjacent to neither a Mersenne prime nor a Fermat...
, 4096, 65536, 262144 .
If n is an even superperfect number then n must be a power of 2, 2k, such that 2k+1-1 is a Mersenne prime
Mersenne prime
In mathematics, a Mersenne number, named after Marin Mersenne , is a positive integer that is one less than a power of two: M_p=2^p-1.\,...
.
It is not known whether there are any odd superperfect numbers. An odd superperfect number n would have to be a square number such that either n or σ(n) is divisible by at least three distinct primes. There are no odd superperfect numbers below 7x1024.
Perfect and superperfect numbers are examples of the wider class of (m,k)-perfect numbers which satisfy

With this notation, perfect numbers are (1,2)-perfect and superperfect numbers are (2,2)-perfect. Other classes of (m,k)-perfect numbers are:
| m | k | (m,k)-perfect numbers | OEIS sequence |
|---|---|---|---|
| 2 | 3 | 8, 21, 512 | |
| 2 | 4 | 15, 1023, 29127 | |
| 2 | 6 | 42, 84, 160, 336, 1344, 86016, 550095, 1376256, 5505024 | |
| 2 | 7 | 24, 1536, 47360, 343976 | |
| 2 | 8 | 60, 240, 960, 4092, 16368, 58254, 61440, 65472, 116508, 466032, 710400, 983040, 1864128, 3932160, 4190208, 67043328, 119304192, 268173312, 1908867072 | |
| 2 | 9 | 168, 10752, 331520, 691200, 1556480, 1612800, 106151936 | |
| 2 | 10 | 480, 504, 13824, 32256, 32736, 1980342, 1396617984, 3258775296 | |
| 2 | 11 | 4404480, 57669920, 238608384 | |
| 2 | 12 | 2200380, 8801520, 14913024, 35206080, 140896000, 459818240, 775898880, 2253189120 | |
| 3 | any | 12, 14, 24, 52, 98, 156, 294, 684, 910, 1368, 1440, 4480, 4788, 5460, 5840, ... | |
| 4 | any | 2, 3, 4, 6, 8, 10, 12, 15, 18, 21, 24, 26, 32, 39, 42, 60, 65, 72, 84, 96, 160, 182, ... |

