Superpattern
Encyclopedia
In mathematics
(and specifically in combinatorics
), k-superpattern is a permutation
of minimal length that contains all permutation patterns of length k.
s of length 3, including 253, 251, 234, 531, 534 and 314. (That is, we take 3 entries at a time, keeping the order preserved.) In each subsequence, we replace the smallest entry with 1, the next largest entry with 2, and the largest with 3. Thus, 253 gets renumbered to 132, 251 to 231, and so on. (If we had chosen subsequences of longer length, we would replace the third-smallest with 3, the fourth-smallest with 4, etc. That is, we apply an order-isomorphism to each subsequence to get a permutation.)
Applying this operation to the six selected subsequences gives 132, 231, 123, 321, 312 and 213. In fact, this list contains all the possible 3-subpatterns, that is, all 6 (3 factorial
) permutations of length 3. From this, we can see that 25314 contains all possible 3-subpatterns. This is one of the two conditions to be a 3-superpattern. The other condition is that there should be no shorter permutation with the same property.
Consider also that in order to have 123 and 321 as subpatterns in the same permutation, by the inclusion-exclusion principle
we need a minimum of 3 + 3 - 1 = 5 numbers (since only one number can be in both the largest increasing sequence
and the largest decreasing sequence). This implies that any permutation which contains both 123 and 321 as subpatterns must be at least 5 digits long. Since 25314 has length 5 it is therefore a 3-superpattern of length 5.
denote the length of k-superpatterns.
The only known lower bound for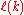
is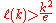 
. This bound follows from the observation that if a permutation of length n contains all permutations of length k as patterns then 
. Applying standard estimates for binomial coefficient
s and factorials (e.g., related to Stirling's approximation
) yields the result.
The upper bound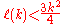
can be shown by probabilistic means.
It is believed that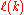
approaches k2/2 in the limit
as
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
(and specifically in combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
), k-superpattern is a permutation
Permutation
In mathematics, the notion of permutation is used with several slightly different meanings, all related to the act of permuting objects or values. Informally, a permutation of a set of objects is an arrangement of those objects into a particular order...
of minimal length that contains all permutation patterns of length k.
Examples
Consider the permutation 25314, which has length 5. It has 10 subsequenceSubsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
s of length 3, including 253, 251, 234, 531, 534 and 314. (That is, we take 3 entries at a time, keeping the order preserved.) In each subsequence, we replace the smallest entry with 1, the next largest entry with 2, and the largest with 3. Thus, 253 gets renumbered to 132, 251 to 231, and so on. (If we had chosen subsequences of longer length, we would replace the third-smallest with 3, the fourth-smallest with 4, etc. That is, we apply an order-isomorphism to each subsequence to get a permutation.)
Applying this operation to the six selected subsequences gives 132, 231, 123, 321, 312 and 213. In fact, this list contains all the possible 3-subpatterns, that is, all 6 (3 factorial
Factorial
In mathematics, the factorial of a non-negative integer n, denoted by n!, is the product of all positive integers less than or equal to n...
) permutations of length 3. From this, we can see that 25314 contains all possible 3-subpatterns. This is one of the two conditions to be a 3-superpattern. The other condition is that there should be no shorter permutation with the same property.
Consider also that in order to have 123 and 321 as subpatterns in the same permutation, by the inclusion-exclusion principle
Inclusion-exclusion principle
In combinatorics, the inclusion–exclusion principle is an equation relating the sizes of two sets and their union...
we need a minimum of 3 + 3 - 1 = 5 numbers (since only one number can be in both the largest increasing sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
and the largest decreasing sequence). This implies that any permutation which contains both 123 and 321 as subpatterns must be at least 5 digits long. Since 25314 has length 5 it is therefore a 3-superpattern of length 5.
Bounds on the length of superpatterns
Let denote the length of k-superpatterns.The only known lower bound for
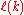is 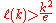. This bound follows from the observation that if a permutation of length n contains all permutations of length k as patterns then . Applying standard estimates for binomial coefficientBinomial coefficient
In mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
s and factorials (e.g., related to Stirling's approximation
Stirling's approximation
In mathematics, Stirling's approximation is an approximation for large factorials. It is named after James Stirling.The formula as typically used in applications is\ln n! = n\ln n - n +O\...
) yields the result.
The upper bound
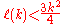can be shown by probabilistic means.It is believed that
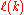approaches k2/2 in the limitLimit
A limit can be:* Limit :** Limit of a function** Limit of a sequence** One-sided limit** Limit superior and limit inferior** Limit of a net** Limit point** Limit ** Direct limit and Inverse limit...
as
.