Subtype polymorphism
Encyclopedia
In programming language theory
, subtyping or subtype polymorphism is a form of type polymorphism
in which a subtype is a datatype that is related to another datatype (the supertype) by some notion of substitutability, meaning that program constructs, typically subroutines or functions, written to operate on elements of the supertype can also operate on elements of the subtype. If S is a subtype of T, the subtyping relation
is often written S <: T, to mean that any term of type S can be safely used in a context where a term of type T is expected. The precise semantics of subtyping crucially depends on the particulars of what "safely used in a context where" means in a given programming language
. The type system
of a programming language essentially defines its own subtyping relation, which may well be trivial.
Because the subtyping relation allows a term to have (belong to) more than one type, subtyping is a form of type polymorphism
, so it is (properly) called subtype polymorphism. In object-oriented programming
subtyping is commonly called just polymorphism (see polymorphism in object-oriented programming
). Subtyping is practically never called this way in type theory
or in functional programming
, where the unqualified use of "polymorphism" usually refers to parametric polymorphism
, as in polymorphic lambda calculus. (Mechanisms similar in purpose, but not identical with parametric polymorphism are known by other names in object-oriented programming, e.g. generics in Java
or templates in C++
.)
Functional programming languages often allow the subtyping of records. Consequently, simply typed lambda calculus
extended with record types is perhaps the simplest theoretical setting in which a useful notion of subtyping may be defined and studied. Because the resulting calculus allows terms to have more than one type, it is no longer a "simple" type theory
. Since functional programming languages, by definition, support function literals, which can also be stored in records, records types with subtyping provide some of the features of object-oriented programming. (Unless references are added to the language, record "objects" are immutable
). Typically, functional programming languages also provide some, usually restricted, form of parametric polymorphism. In a theoretical setting, it is desirable to study the interaction of the two features; a common theoretical setting is system F<:. Various calculi that attempt to capture the theoretical properties of object-oriented programming may be derived from system F<:.
The concept of subtyping is related to the linguistic notions of hypernymy and holonymy
. It is also related to the concept of bounded quantification
in mathematical logic. Subtyping should not be confused with the notion of (class or object) inheritance
from object-oriented languages; subtyping is a relation between types (interfaces in object-oriented parlance) whereas inheritance is a relation between implementations stemming from a language feature that allows new objects to be created from existing ones. In a number of object-oriented languages, subtyping is called interface inheritance.
derivatives. The first formal treatments of subtyping were given by John C. Reynolds
in 1980 who used category theory
to formalize implicit conversions, and Luca Cardelli
(1985).
The concept of subtyping has gained visibility (and synonymy with polymorphism in some circles) with the mainstream adoption of object-oriented programming. In this context, the principle of safe substitution is often called the Liskov substitution principle
, after Barbara Liskov
who popularized it in a keynote
address at a conference on object-oriented programming in 1987. Because it must consider mutable objects, the ideal notion of subtyping defined by Liskov and Jeannette Wing
, called behavioral subtyping is considerably stronger than what can be implemented in a type checker. (see the section on function types for details)
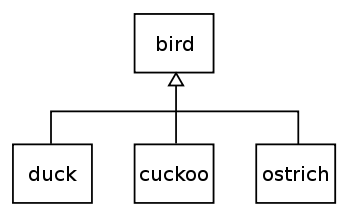A simple practical example of subtypes is shown in the diagram, right. The type "bird" has three subtypes "duck", "cuckoo" and "ostrich". Conceptually, each of these is a variety of the basic "bird" that inherits many "bird" characteristics but has some specific differences. The UML
notation is used in this diagram, with open-headed arrows showing the direction and type of the relationship between the supertype and its subtypes.
As a more practical example, a language might allow floating point values to be used wherever integer values are expected (
Programmers may take advantage of subtyping to write code in a more abstract manner
than would be possible without it. Consider the following example:
function max (x as Number, y as Number) is
if x < y then
return y
else
return x
end
If integer and real are both subtypes of
Subtyping in type theory is characterized by the fact that any expression of type A may also be given type B if A<:B; the formal typing rule that codifies this is known as the subsumption rule.
, in which only types declared in a certain way may be subtypes of each other, and structural subtyping
, in which the structure of two types determines whether or not one is a subtype of the other. The class-based object-oriented subtyping described above is nominal; a structural subtyping rule for an object-oriented language might say that if objects of type A can handle all of the messages that objects of type B can handle (that is, if they define all the same method
s), then A is a subtype of B regardless of whether either inherits
from the other. Sound structural subtyping rules for types other than object types are also well known.
Implementations of programming languages with subtyping fall into two general classes: inclusive implementations, in which the representation of any value of type A also represents the same value at type B if A<:B, and coercive implementations, in which a value of type A can be automatically converted into one of type B. The subtyping induced by subclassing in an object-oriented language is usually inclusive; subtyping relations that relate integers and floating-point numbers, which are represented differently, are usually coercive.
In almost all type systems that define a subtyping relation, it is reflexive (meaning A<:A for any type A) and transitive (meaning that if A<:B and B<:C then A<:C). This makes it a preorder
on types.
give rise to the concepts of width and depth subtyping. These express two different ways of obtaining a new type of record that allows the same operations as the original record type.
Recall that a record is a collection of (named) fields. Since a subtype is a type which allows all operations allowed on the original type, a record subtype should support the same operations on the fields as the original type supported.
One kind of way to achieve such support, called width subtyping, adds more fields to the record. More formally, every (named) field appearing in the width supertype will appear in the width subtype. Thus, any operation feasible on the supertype will be supported by the subtype.
The second method, called depth subtyping, replaces the various fields with their subtypes. That is, the fields of the subtype are subtypes of the fields of the supertype. Since any operation supported for a field in the supertype is supported for its subtype, any operation feasible on the record supertype is supported by the record subtype. Depth subtyping only makes sense for immutable records: for example, you can assign 1.5 to the 'x' field of a real point (a record with two real fields), but you can't do the same to the 'x' field of an integer point (which, however, is a deep subtype of the real point type) because 1.5 is not an integer.
Subyping of records can be defined in System F<:, which combines parametric polymorphism
with subtyping of record types and is a theoretical basis for many functional programming languages that support both features.
Some systems also support subtyping of labeled disjoint union
types (such as algebraic data type
s). The rule for width subtyping is reversed: every tag appearing in the width subtype must appear in the width supertype.
because the subtyping relation is reversed for it, whereas the return type is covariant
. (Informally, this reversal occurs because the refined type is "more liberal" in the types it accepts and "more conservative" in the type it returns.)
In languages that allow side effects, like most object-oriented languages, subtyping is generally not sufficient to guarantee that a function can be safely used in the context of another. Liskov's work in this area focused on behavioral subtyping, which besides the type system safety discussed in this article also requires that subtypes preserve all invariants
guaranteed by the supertypes in some contract
. This definition of subtyping is generally undecidable
, so it cannot be verified by a type checker.
The subtyping of mutable references is similar to the treatment of function arguments and return values. Write-only references (or sinks) are contravariant, like function arguments; read-only references (or sources) are covariant, like return values. Mutable references which act as both sources and sinks are invariant.
functions from subtype to supertype. For each subtyping relationship (S <: T), a coercion function coerce: S → T is provided, and any object s of type S is regarded as the object coerceS → T(s) of type T. A coercion function may be defined by composition: if S <: T and T <: U then s may be regarded as an object of type u under the compound coercion (coerceT → U ∘ coerceS → T). The type coercion from a type to itself coerceT → T is the identity function
idT
Coercion functions for records and disjoint union subtypes may be defined componentwise; in the case of width-extended records, type coercion simply discards any components which are not defined in the supertype. The type coercion for function types may be given by f'(s) = coerceS2 → T2(f(coerceT1 → S1(t))), reflecting the contravariance of function arguments and covariance of return values.
The coercion function is uniquely determined given the subtype and supertype. Thus, when multiple subtyping relationships are defined, one must be careful to guarantee that all type coercions are coherent. For instance, if an integer such as 2 : int can be coerced to a floating point number (say, 2.0 : float), then it is not admissible to coerce 2.1 : float to 2 : int, because the compound coercion coercefloat → float given by coerceint → float ∘ coercefloat → int would then be distinct from the identity coercion idfloat.
" in many imperative programming languages.
Programming language theory
Programming language theory is a branch of computer science that deals with the design, implementation, analysis, characterization, and classification of programming languages and their individual features. It falls within the discipline of computer science, both depending on and affecting...
, subtyping or subtype polymorphism is a form of type polymorphism
Type polymorphism
In computer science, polymorphism is a programming language feature that allows values of different data types to be handled using a uniform interface. The concept of parametric polymorphism applies to both data types and functions...
in which a subtype is a datatype that is related to another datatype (the supertype) by some notion of substitutability, meaning that program constructs, typically subroutines or functions, written to operate on elements of the supertype can also operate on elements of the subtype. If S is a subtype of T, the subtyping relation
Binary relation
In mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
is often written S <: T, to mean that any term of type S can be safely used in a context where a term of type T is expected. The precise semantics of subtyping crucially depends on the particulars of what "safely used in a context where" means in a given programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
. The type system
Type system
A type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...
of a programming language essentially defines its own subtyping relation, which may well be trivial.
Because the subtyping relation allows a term to have (belong to) more than one type, subtyping is a form of type polymorphism
Type polymorphism
In computer science, polymorphism is a programming language feature that allows values of different data types to be handled using a uniform interface. The concept of parametric polymorphism applies to both data types and functions...
, so it is (properly) called subtype polymorphism. In object-oriented programming
Object-oriented programming
Object-oriented programming is a programming paradigm using "objects" – data structures consisting of data fields and methods together with their interactions – to design applications and computer programs. Programming techniques may include features such as data abstraction,...
subtyping is commonly called just polymorphism (see polymorphism in object-oriented programming
Polymorphism in object-oriented programming
Subtype polymorphism, almost universally called just polymorphism in the context of object-oriented programming, is the ability to create a variable, a function, or an object that has more than one form. The word derives from the Greek "πολυμορφισμός" meaning "having multiple forms"...
). Subtyping is practically never called this way in type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
or in functional programming
Functional programming
In computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
, where the unqualified use of "polymorphism" usually refers to parametric polymorphism
Parametric polymorphism
In programming languages and type theory, parametric polymorphism is a way to make a language more expressive, while still maintaining full static type-safety. Using parametric polymorphism, a function or a data type can be written generically so that it can handle values identically without...
, as in polymorphic lambda calculus. (Mechanisms similar in purpose, but not identical with parametric polymorphism are known by other names in object-oriented programming, e.g. generics in Java
Generics in Java
Generics are a facility of generic programming that was added to the Java programming language in 2004 as part of J2SE 5.0. They allow "a type or method to operate on objects of various types while providing compile-time type safety." A common use of this feature is when using a Java Collection...
or templates in C++
Template (programming)
Templates are a feature of the C++ programming language that allow functions and classes to operate with generic types. This allows a function or class to work on many different data types without being rewritten for each one....
.)
Functional programming languages often allow the subtyping of records. Consequently, simply typed lambda calculus
Simply typed lambda calculus
The simply typed lambda calculus , a formof type theory, is a typed interpretation of the lambda calculus with only one type constructor: \to that builds function types. It is the canonical and simplest example of a typed lambda calculus...
extended with record types is perhaps the simplest theoretical setting in which a useful notion of subtyping may be defined and studied. Because the resulting calculus allows terms to have more than one type, it is no longer a "simple" type theory
Type theory
In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...
. Since functional programming languages, by definition, support function literals, which can also be stored in records, records types with subtyping provide some of the features of object-oriented programming. (Unless references are added to the language, record "objects" are immutable
Immutable object
In object-oriented and functional programming, an immutable object is an object whose state cannot be modified after it is created. This is in contrast to a mutable object, which can be modified after it is created...
). Typically, functional programming languages also provide some, usually restricted, form of parametric polymorphism. In a theoretical setting, it is desirable to study the interaction of the two features; a common theoretical setting is system F<:. Various calculi that attempt to capture the theoretical properties of object-oriented programming may be derived from system F<:.
The concept of subtyping is related to the linguistic notions of hypernymy and holonymy
Holonymy
Holonymy is a semantic relation. Holonymy defines the relationship between a term denoting the whole and a term denoting a part of, or a member of, the whole. That is,...
. It is also related to the concept of bounded quantification
Bounded quantification
In type theory, bounded quantification refers to universal or existential quantifiers which are restricted to range only over the subtypes of a particular type. Bounded quantification is an interaction of parametric polymorphism with subtyping...
in mathematical logic. Subtyping should not be confused with the notion of (class or object) inheritance
Inheritance (computer science)
In object-oriented programming , inheritance is a way to reuse code of existing objects, establish a subtype from an existing object, or both, depending upon programming language support...
from object-oriented languages; subtyping is a relation between types (interfaces in object-oriented parlance) whereas inheritance is a relation between implementations stemming from a language feature that allows new objects to be created from existing ones. In a number of object-oriented languages, subtyping is called interface inheritance.
Origins
The notion of subtyping in programming languages dates back to the 1960s; it was introduced in SimulaSimula
Simula is a name for two programming languages, Simula I and Simula 67, developed in the 1960s at the Norwegian Computing Center in Oslo, by Ole-Johan Dahl and Kristen Nygaard...
derivatives. The first formal treatments of subtyping were given by John C. Reynolds
John C. Reynolds
John C. Reynolds is an American computer scientist.John Reynolds studied at Purdue University and then earned a PhD in theoretical physics from Harvard University in 1961. He was Professor of Information science at Syracuse University from 1970 to 1986. Since then he has been Professor of Computer...
in 1980 who used category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
to formalize implicit conversions, and Luca Cardelli
Luca Cardelli
Luca Cardelli is an Italian computer scientist who is currently an Assistant Director at Microsoft Research in Cambridge, UK. Cardelli is well-known for his research in type theory and operational semantics. Among other contributions he implemented the first compiler for the functional programming...
(1985).
The concept of subtyping has gained visibility (and synonymy with polymorphism in some circles) with the mainstream adoption of object-oriented programming. In this context, the principle of safe substitution is often called the Liskov substitution principle
Liskov substitution principle
Substitutability is a principle in object-oriented programming. It states that, in a computer program, if S is a subtype of T, then objects of type T may be replaced with objects of type S without altering any of the desirable properties of that program...
, after Barbara Liskov
Barbara Liskov
Barbara Liskov is a computer scientist. She is currently the Ford Professor of Engineering in the MIT School of Engineering's Electrical Engineering and Computer Science department and an Institute Professor at the Massachusetts Institute of Technology.-Life and career:She earned her BA in...
who popularized it in a keynote
Keynote
A keynote in literature, music, or public speaking establishes the principal underlying theme. In corporate or commercial settings, greater importance is attached to the delivery of a keynote speech or keynote address...
address at a conference on object-oriented programming in 1987. Because it must consider mutable objects, the ideal notion of subtyping defined by Liskov and Jeannette Wing
Jeannette Wing
Jeannette Marie Wing is a computer science professor at Carnegie Mellon University, Pittsburgh, Pennsylvania, United States, and assistant director for Computer and Information Science and Engineering at the NSF....
, called behavioral subtyping is considerably stronger than what can be implemented in a type checker. (see the section on function types for details)
Examples
Unified Modeling Language
Unified Modeling Language is a standardized general-purpose modeling language in the field of object-oriented software engineering. The standard is managed, and was created, by the Object Management Group...
notation is used in this diagram, with open-headed arrows showing the direction and type of the relationship between the supertype and its subtypes.
As a more practical example, a language might allow floating point values to be used wherever integer values are expected (
Float <: Integer), or it might define a generic type Number as a common supertype of integers and the reals. In this second case, we only have Integer <: Number and Float <: Number, but Integer and Float are not subtypes of each other.Programmers may take advantage of subtyping to write code in a more abstract manner
Abstraction principle (programming)
In software engineering and programming language theory, the abstraction principle is a basic dictum that aims to reduce duplication of information in a program whenever practical by making use of abstractions provided by the programming language or software libraries...
than would be possible without it. Consider the following example:
function max (x as Number, y as Number) is
if x < y then
return y
else
return x
end
If integer and real are both subtypes of
Number, and an operator of comparison with an arbitrary Number is defined for both types, then values of either type can be passed to this function. However, the very possibility of implementing such an operator highly constrains the Number type (for example, one can't compare an integer with a complex number), and actually only comparing integers with integers and reals with reals makes sense. Rewriting this function so that it would only accept 'x' and 'y' of the same type requires F-Bounded Polymorphism.Subtyping in type theory is characterized by the fact that any expression of type A may also be given type B if A<:B; the formal typing rule that codifies this is known as the subsumption rule.
Subtyping schemes
Type theorists make a distinction between nominal subtypingNominative type system
In computer science, a nominal or nominative type system is a major class of type system, in which compatibility and equivalence of data types is determined by explicit declarations and/or the name of the types. Nominative systems are used to determine if types are equivalent, as well as if a type...
, in which only types declared in a certain way may be subtypes of each other, and structural subtyping
Structural type system
A structural type system is a major class of type system, in which type compatibility and equivalence are determined by the type's structure, and not by other characteristics such as its name or place of declaration. Structural systems are used to determine if types are equivalent and whether a...
, in which the structure of two types determines whether or not one is a subtype of the other. The class-based object-oriented subtyping described above is nominal; a structural subtyping rule for an object-oriented language might say that if objects of type A can handle all of the messages that objects of type B can handle (that is, if they define all the same method
Method (computer science)
In object-oriented programming, a method is a subroutine associated with a class. Methods define the behavior to be exhibited by instances of the associated class at program run time...
s), then A is a subtype of B regardless of whether either inherits
Inheritance (computer science)
In object-oriented programming , inheritance is a way to reuse code of existing objects, establish a subtype from an existing object, or both, depending upon programming language support...
from the other. Sound structural subtyping rules for types other than object types are also well known.
Implementations of programming languages with subtyping fall into two general classes: inclusive implementations, in which the representation of any value of type A also represents the same value at type B if A<:B, and coercive implementations, in which a value of type A can be automatically converted into one of type B. The subtyping induced by subclassing in an object-oriented language is usually inclusive; subtyping relations that relate integers and floating-point numbers, which are represented differently, are usually coercive.
In almost all type systems that define a subtyping relation, it is reflexive (meaning A<:A for any type A) and transitive (meaning that if A<:B and B<:C then A<:C). This makes it a preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
on types.
Record types
Types of recordsRecord (computer science)
In computer science, a record is an instance of a product of primitive data types called a tuple. In C it is the compound data in a struct. Records are among the simplest data structures. A record is a value that contains other values, typically in fixed number and sequence and typically indexed...
give rise to the concepts of width and depth subtyping. These express two different ways of obtaining a new type of record that allows the same operations as the original record type.
Recall that a record is a collection of (named) fields. Since a subtype is a type which allows all operations allowed on the original type, a record subtype should support the same operations on the fields as the original type supported.
One kind of way to achieve such support, called width subtyping, adds more fields to the record. More formally, every (named) field appearing in the width supertype will appear in the width subtype. Thus, any operation feasible on the supertype will be supported by the subtype.
The second method, called depth subtyping, replaces the various fields with their subtypes. That is, the fields of the subtype are subtypes of the fields of the supertype. Since any operation supported for a field in the supertype is supported for its subtype, any operation feasible on the record supertype is supported by the record subtype. Depth subtyping only makes sense for immutable records: for example, you can assign 1.5 to the 'x' field of a real point (a record with two real fields), but you can't do the same to the 'x' field of an integer point (which, however, is a deep subtype of the real point type) because 1.5 is not an integer.
Subyping of records can be defined in System F<:, which combines parametric polymorphism
Parametric polymorphism
In programming languages and type theory, parametric polymorphism is a way to make a language more expressive, while still maintaining full static type-safety. Using parametric polymorphism, a function or a data type can be written generically so that it can handle values identically without...
with subtyping of record types and is a theoretical basis for many functional programming languages that support both features.
Some systems also support subtyping of labeled disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
types (such as algebraic data type
Algebraic data type
In computer programming, particularly functional programming and type theory, an algebraic data type is a datatype each of whose values is data from other datatypes wrapped in one of the constructors of the datatype. Any wrapped datum is an argument to the constructor...
s). The rule for width subtyping is reversed: every tag appearing in the width subtype must appear in the width supertype.
Function types
If T1 → T2 is a function type then a subtype of it is any function S1 → S2 with the property that T1 <: S1 and S2 <: T2. The argument type of S1 → S2 is said to be contravariantCovariance and contravariance (computer science)
Within the type system of a programming language, covariance and contravariance refers to the ordering of types from narrower to wider and their interchangeability or equivalence in certain situations ....
because the subtyping relation is reversed for it, whereas the return type is covariant
Covariance and contravariance (computer science)
Within the type system of a programming language, covariance and contravariance refers to the ordering of types from narrower to wider and their interchangeability or equivalence in certain situations ....
. (Informally, this reversal occurs because the refined type is "more liberal" in the types it accepts and "more conservative" in the type it returns.)
In languages that allow side effects, like most object-oriented languages, subtyping is generally not sufficient to guarantee that a function can be safely used in the context of another. Liskov's work in this area focused on behavioral subtyping, which besides the type system safety discussed in this article also requires that subtypes preserve all invariants
Invariant (computer science)
In computer science, a predicate is called an invariant to a sequence of operations provided that: if the predicate is true before starting the sequence, then it is true at the end of the sequence.-Use:...
guaranteed by the supertypes in some contract
Design by contract
Design by contract , also known as programming by contract and design-by-contract programming, is an approach to designing computer software...
. This definition of subtyping is generally undecidable
Undecidable problem
In computability theory and computational complexity theory, an undecidable problem is a decision problem for which it is impossible to construct a single algorithm that always leads to a correct yes-or-no answer....
, so it cannot be verified by a type checker.
The subtyping of mutable references is similar to the treatment of function arguments and return values. Write-only references (or sinks) are contravariant, like function arguments; read-only references (or sources) are covariant, like return values. Mutable references which act as both sources and sinks are invariant.
Coercions
In coercive subtyping systems, subtypes are defined by implicit type conversionType conversion
In computer science, type conversion, typecasting, and coercion are different ways of, implicitly or explicitly, changing an entity of one data type into another. This is done to take advantage of certain features of type hierarchies or type representations...
functions from subtype to supertype. For each subtyping relationship (S <: T), a coercion function coerce: S → T is provided, and any object s of type S is regarded as the object coerceS → T(s) of type T. A coercion function may be defined by composition: if S <: T and T <: U then s may be regarded as an object of type u under the compound coercion (coerceT → U ∘ coerceS → T). The type coercion from a type to itself coerceT → T is the identity function
Identity function
In mathematics, an identity function, also called identity map or identity transformation, is a function that always returns the same value that was used as its argument...
idT
Coercion functions for records and disjoint union subtypes may be defined componentwise; in the case of width-extended records, type coercion simply discards any components which are not defined in the supertype. The type coercion for function types may be given by f'(s) = coerceS2 → T2(f(coerceT1 → S1(t))), reflecting the contravariance of function arguments and covariance of return values.
The coercion function is uniquely determined given the subtype and supertype. Thus, when multiple subtyping relationships are defined, one must be careful to guarantee that all type coercions are coherent. For instance, if an integer such as 2 : int can be coerced to a floating point number (say, 2.0 : float), then it is not admissible to coerce 2.1 : float to 2 : int, because the compound coercion coercefloat → float given by coerceint → float ∘ coercefloat → int would then be distinct from the identity coercion idfloat.
Intersection and union types
Union types should not to be confused with sum types, the anonymous version of which are called a "unionsUnion (computer science)
In computer science, a union is a value that may have any of several representations or formats; or a data structure that consists of a variable which may hold such a value. Some programming languages support special data types, called union types, to describe such values and variables...
" in many imperative programming languages.
See also
- Polymorphism in object-oriented programmingPolymorphism in object-oriented programmingSubtype polymorphism, almost universally called just polymorphism in the context of object-oriented programming, is the ability to create a variable, a function, or an object that has more than one form. The word derives from the Greek "πολυμορφισμός" meaning "having multiple forms"...
for a gentler introduction in that context - A derived typeDerived typeIn computer science, derived type can mean:* a composite data type, one built out of other types* a subtype or derived class...
is a typeData typeIn computer programming, a data type is a classification identifying one of various types of data, such as floating-point, integer, or Boolean, that determines the possible values for that type; the operations that can be done on values of that type; the meaning of the data; and the way values of...
given a new type but structurally the same as the original type. It may or may not be a subtype depending on the type system. - Contravariance in Covariance and contravariance (computer science)Covariance and contravariance (computer science)Within the type system of a programming language, covariance and contravariance refers to the ordering of types from narrower to wider and their interchangeability or equivalence in certain situations ....
- The circle-ellipse problemCircle-ellipse problemThe circle-ellipse problem in software development illustrates a number of pitfalls which can arise when using subtype polymorphism in object modelling...
for the perils of subtyping variable-types on the same basis as value-types - class-based programmingClass-based programmingClass-based programming, or more commonly class-orientation, refers to the style of object-oriented programming in which inheritance is achieved by defining classes of objects, as opposed to the objects themselves .The most popular and developed model of OOP is a class-based model, as opposed to an...
for an example of a problem when one confuses subtyping with subclassing. - Top typeTop typeThe top type in type theory, commonly abbreviated as top or by the down tack symbol , is the universal type—that type which contains every possible object in the type system of interest. The top type is sometimes called the universal supertype as all other types in any given type system are...
- refinement type
- superclass and subclass
Further reading
- John C. ReynoldsJohn C. ReynoldsJohn C. Reynolds is an American computer scientist.John Reynolds studied at Purdue University and then earned a PhD in theoretical physics from Harvard University in 1961. He was Professor of Information science at Syracuse University from 1970 to 1986. Since then he has been Professor of Computer...
, Theories of programming languages, Cambridge University Press, 1998, ISBN 0521594146, chapter 16. - Martín AbadiMartín AbadiMartín Abadi is an argentinian computer scientist, currently working at the University of California, Santa Cruz and Microsoft Research. He earned his Ph.D...
, Luca CardelliLuca CardelliLuca Cardelli is an Italian computer scientist who is currently an Assistant Director at Microsoft Research in Cambridge, UK. Cardelli is well-known for his research in type theory and operational semantics. Among other contributions he implemented the first compiler for the functional programming...
, A theory of objects, Springer, 1996, ISBN 0387947752. Section 8.6 contrast the subtyping of records and objects.