In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, in the field of ordinary differential equation

Ordinary differential equation

In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....

s, Sturm separation theorem, named after Jacques Charles François Sturm, describes the location of roots of homogeneous

Homogeneous differential equation

The term homogeneous differential equation has several distinct meanings.One meaning is that a first-order ordinary differential equation is homogeneous if it has the formwhere F is a homogeneous function of degree zero; that is to say, that F = F.In a related, but distinct, usage, the term linear...

 second order linear differential equation

Linear differential equation

Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...

s. Basically the theorem states that given two linear independent solutions of such an equation the zeros of the two solutions are alternating.

Sturm separation theorem

Given a homogeneous second order linear differential equation and two continuous linear independent solutions u(x) and v(x) with x₀ and x₁ successive roots of u(x), then v(x) has exactly one root in the open interval ]x₀, x₁[. It is a special case of the Sturm-Picone comparison theorem

Sturm-Picone comparison theorem

In mathematics, in the field of ordinary differential equations, the Sturm–Picone comparison theorem, named after Jacques Charles François Sturm and Mauro Picone, is a classical theorem which provides criteria for the oscillation and non-oscillation of solutions of certain linear differential...

.

Proof

The proof is by contradiction. Assume that v has no zeros in ]x₀, x₁[. Since u and v are linearly independent, v cannot vanish at either x₀ or x₁, so the quotient u / v is well-defined on the closed interval [x₀, x₁], and it is zero at x₀ and x₁. Hence, by Rolle's theorem

Rolle's theorem

In calculus, Rolle's theorem essentially states that a differentiable function which attains equal values at two distinct points must have a point somewhere between them where the first derivative is zero.-Standard version of the theorem:If a real-valued function ƒ is continuous on a closed...

, there is a point ξ between x₀ and x₁ where
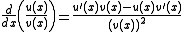
vanishes. Hence, , which implies that u and v are linearly dependent. This contradicts our assumption, and thus, v has to have at least one zero between x₀ and x₁.

On the other hand, there can be only one zero between x₀ and x₁, because otherwise v would have two zeros and there would be no zeros of u in between, and it was just proved that this is impossible .

An alternative proof

Since and are linearly independent it follows that the Wronskian 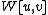must satisfy 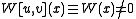for all where the differential equation is defined, say . Without loss of generality, suppose that 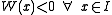. Then
So at
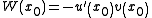
and either 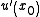and are both positive or both negative. Without loss of generality, suppose that they are both positive. Now, at
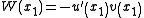
and since and are successive zeros of it causes . Thus, to keep we must have . We see this by observing that if then would be increasing (away from the -axis), which would never lead to a zero at 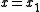. So for a zero to occur at at most 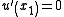(i.e., 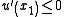and it turns out, by our result from the Wronskian that ). So somewhere in the interval 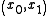the sign of changed. By the Intermediate Value Theorem

Intermediate value theorem

In mathematical analysis, the intermediate value theorem states that for each value between the least upper bound and greatest lower bound of the image of a continuous function there is at least one point in its domain that the function maps to that value....

there exists 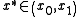such that .

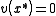By the same reasoning as in the first proof, can have at most one zero for 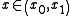.