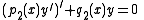Sturm-Picone comparison theorem
Encyclopedia
In mathematics
, in the field of ordinary differential equation
s, the Sturm–Picone comparison theorem, named after Jacques Charles François Sturm and Mauro Picone
, is a classical theorem which provides criteria for the oscillation and non-oscillation of solutions of certain linear differential equation
s.
be two homogeneous linear second order differential equations in self-adjoint form with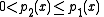
and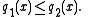
Let u be a non-trivial solution of (1) with successive roots at z1 and z2 and let v be a non-trivial solution of (2). Then one of the following properties holds.
In the special case where both equations are equal one obtains the Sturm separation theorem
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, in the field of ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s, the Sturm–Picone comparison theorem, named after Jacques Charles François Sturm and Mauro Picone
Mauro Picone
Mauro Picone was an Italian mathematician. He is known for the Picone identity, for the Sturm-Picone comparison theorem and for being the founder of the Istituto Nazionale per le Applicazioni del Calcolo, presently named after him...
, is a classical theorem which provides criteria for the oscillation and non-oscillation of solutions of certain linear differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
s.
Sturm–Picone comparison theorem
Letbe two homogeneous linear second order differential equations in self-adjoint form with
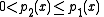
and
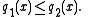
Let u be a non-trivial solution of (1) with successive roots at z1 and z2 and let v be a non-trivial solution of (2). Then one of the following properties holds.
- There exists an x in [z1, z2] such that v(x) = 0; or
- there exists a λ in R such that v(x) = λ u(x).
In the special case where both equations are equal one obtains the Sturm separation theorem
Sturm separation theorem
In mathematics, in the field of ordinary differential equations, Sturm separation theorem, named after Jacques Charles François Sturm, describes the location of roots of homogeneous second order linear differential equations...
.