In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

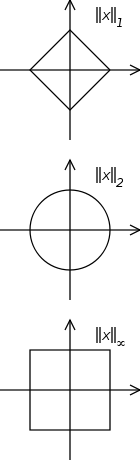
, a strictly convex space is a normed

Normed vector space

In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....

 topological vector space

Topological vector space

In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...

 (V, || ||) for which the unit ball is a strictly convex set

Convex set

In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...

. Put another way, a strictly convex space is one for which, given any two points x and y in the boundary

Boundary (topology)

In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...

 ∂B of the unit ball B of V, the affine line L(x, y) passing through x and y meets ∂B only at x and y. Strict convexity is somewhere between an inner product space

Inner product space

In mathematics, an inner product space is a vector space with an additional structure called an inner product. This additional structure associates each pair of vectors in the space with a scalar quantity known as the inner product of the vectors...

 (all inner product spaces are strictly convex) and a general normed space (all strictly convex normed spaces are normed spaces) in terms of structure. It also guarantees the uniqueness of a best approximation to an element in X (strictly convex) out of Y (a subspace of X) if indeed such an approximation exists.

Properties

• A Banach space
  Banach space
  In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
  
   (V, || ||) is strictly convex if and only if
  If and only if
  In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
  
   the modulus of convexity δ for (V, || ||) satisfies δ(2) = 1.

• A Banach space
  Banach space
  In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
  
   (V, || ||) is strictly convex if and only if x ≠ y and || x || = || y || = 1 together imply that || x + y || < 2.

• A Banach space
  Banach space
  In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
  
   (V, || ||) is strictly convex if and only if x ≠ y and || x || = || y || = 1 together imply that || αx + (1 − α)y || < 1 for all 0 < α < 1.

• A Banach space
  Banach space
  In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
  
  (V, || ||) is strictly convex if and only if x ≠ 0 and y ≠ 0 and || x + y || = || x || + || y || together imply that x = cy for some constant c > 0.