The stretched exponential function is a generalization of the exponential function

Exponential function

In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...

 with one additional parameter, the stretching exponent β:.
In most applications, it is meaningful only for arguments t between 0 and +∞. With β=1, the usual exponential function is recovered. With β between 0 and 1,
the graph of φ(t) versus log(t) is characteristically stretched, whence the name of the function.

The compressed exponential function (with β>1) has less practical importance, with the notable exception of β=2, which gives the normal distribution.

In mathematics, the stretched exponential is also known as the complementary cumulative Weibull distribution. Furthermore, the stretched exponential is the characteristic function

Characteristic state function

The characteristic state function in statistical mechanics refers to a particular relationship between the partition function of an ensemble.In particular, if the partition function P satisfiesP = \exp or P = \exp...

 (basically the Fourier transform

Fourier transform

In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

) of the Lévy symmetric alpha-stable distribution.

In physics, the stretched exponential function is often used as a phenomenological description of relaxation in disordered systems. It was first introduced by Rudolf Kohlrausch

Rudolf Kohlrausch

Rudolf Hermann Arndt Kohlrausch was a German physicist.-Biography:He was a native of Göttingen, the son of educator Heinrich Friedrich Theodor Kohlrausch...

 in 1854 to describe the discharge of a capacitor;
therefore it is also called the Kohlrausch function. In 1970, G. Williams and D.C. Watts used the Fourier transform

Fourier transform

In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...

 of the stretched exponential to describe dielectric spectra of polymers;
in this context, the stretched exponential or its Fourier transform are also called the Kohlrausch-Williams-Watts (KWW) function.

Distribution function

In some fields of physics, apparent stretched exponential behaviour is often motivated as a linear superposition of simple exponential decays. This requires a nontrivial distribution of relaxation times, ρ(u), which is implicitly defined by

.

Alternatively, a distribution

is used.

ρ can be computed from the series expansion:

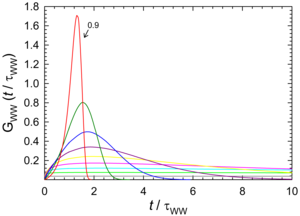
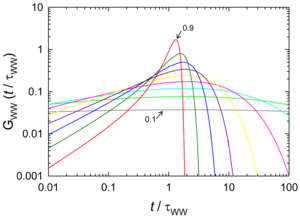
Figure 2 shows the same results plotted in both a linear

Linear

In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...

 and a log

Logarithm

The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...

 representation. The curves converge to a Dirac delta function

Dirac delta function

The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...

 peaked at u=1 as β approaches 1, corresponding to the simple exponential function.

Figure 2. Linear and log-log plots of the stretched exponential distribution function vs for values of the stretching parameter β between 0.1 and 0.9.

Mean relaxation time

Following the usual physical interpretation, we interpret the function argument t as a time. The area under the curve φ(t) is therefore interpreted as a mean relaxation time. One finds

where is the gamma function

Gamma function

In mathematics, the gamma function is an extension of the factorial function, with its argument shifted down by 1, to real and complex numbers...

. For exponential decay, is recovered.

Higher moments

The higher moments

Moment (mathematics)

In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...

 of the stretched exponential function are:

.

They are closely related to the moments of the distribution of simple-exponential relaxation times,

.

The first logarithmic moment of the distribution of simple-exponential relaxation times is

where Eu is the Euler constant.

Fourier Transform

To describe results from spectroscopy or inelastic scattering, the sine or cosine Fourier transform of the stretched exponential is needed. It must be calculated either by numeric integration, or from a series expansion. For practical purposes, the Fourier transform may be approximated by the Havriliak-Negami function

Havriliak-Negami relaxation

Havriliak–Negami relaxation is an empirical modification of the Debye relaxation model, accounting for the asymmetry and broadness of the dielectric dispersion curve...

.

History and further applications

As said in the introduction, the stretched exponential was introduced by the German

Germans

The Germans are a Germanic ethnic group native to Central Europe. The English term Germans has referred to the German-speaking population of the Holy Roman Empire since the Late Middle Ages....

 physicist

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

 Rudolf Kohlrausch

Rudolf Kohlrausch

Rudolf Hermann Arndt Kohlrausch was a German physicist.-Biography:He was a native of Göttingen, the son of educator Heinrich Friedrich Theodor Kohlrausch...

 in 1854 to describe the discharge of a capacitor (Leyden jar

Leyden jar

A Leyden jar, or Leiden jar, is a device that "stores" static electricity between two electrodes on the inside and outside of a jar. It was invented independently by German cleric Ewald Georg von Kleist on 11 October 1745 and by Dutch scientist Pieter van Musschenbroek of Leiden in 1745–1746. The...

) that used glass as dielectric medium. The next documented usage is by Friedrich Kohlrausch

Friedrich Kohlrausch

Friedrich Wilhelm Georg Kohlrausch was a German physicist who investigated the conductive properties of electrolytes and contributed to knowledge of their behaviour...

, son of Rudolf, to describe torsional relaxation. A. Werner used it in 1907 to describe complex luminescence decays; Theodor Förster

Theodor Förster

Theodor Förster was a German physical chemist.Theodor Förster undertook a Ph.D. under Erwin Madelung at the University of Frankfurt am Main . In the same year he joined the Nazi Party and the SA. After his habilitation he became a lecturer in Leipzig...

in 1949 as the fluorescence decay law of electronic energy donors.

Outside condensed matter physics, the stretched exponential has been used to describe the removal rates of small, stray bodies in the solar system,
and the diffusion-weighted MRI signal in the brain.

External links

• J. Wuttke: libkww C library to compute the Fourier transform of the stretched exponential function