
Streaming algorithm
Encyclopedia
In computer science
, streaming algorithms are algorithms for
processing data streams in which the input is presented as a sequence of
items and can be examined in only a few passes (typically just one). These
algorithms have limited memory available to them (much less than the input
size) and also limited processing time per item.
These constraints may mean that an algorithm produces an approximate answer based on a summary or "sketch" of the data stream in memory.
Paterson as well as Flajolet and
Martin, the field of streaming
algorithms was first formalized and popularized in a paper by Noga Alon
,
Yossi Matias, and Mario Szegedy
.
For this paper, the authors later won the Gödel Prize
in 2005 "for their foundational
contribution to streaming algorithms." There has since been a large body
of work centered around data streaming algorithms that spans a diverse
spectrum of computer science fields such as theory, databases, networking,
and natural language processing.
to be operated on are not available for random access from disk or
memory, but rather arrive as one or more continuous data streams.
Streams can be denoted as an ordered sequence of points (or "updates") that must be accessed in order and can be read only once or a small number of times.
Much of the streaming literature is concerned with computing statistics on
frequency distributions that are too large to be stored. For this class of
problems, there is a vector
(initialized to the zero vector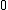 ) that has updates
) that has updates
presented to it in a stream. The goal of these algorithms is to compute
functions of using considerably less space than it
using considerably less space than it
would take to represent precisely. There are two
precisely. There are two
common models for updating such streams, called the "cash register" and
"turnstile" models.
In the cash register model each update is of the form , so that
, so that  is incremented by some positive
is incremented by some positive
integer . A notable special case is when
. A notable special case is when 
(only unit insertions are permitted).
In the turnstile model each update is of the form , so that
, so that 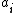 is incremented by some (possible
is incremented by some (possible
negative) integer . In the "strict turnstile" model, no
. In the "strict turnstile" model, no
 at any time may be less than zero.
at any time may be less than zero.
Several papers also consider the "sliding window" model. In this model,
the function of interest is computing over a fixed-size window in the
stream. As the stream progresses, items from the end of the window are
removed from consideration while new items from the stream take their
place.
Besides the above frequency-based problems, some other types of problems
have also been studied. Many graph problems are solved in the setting
where the adjacency matrix
or the adjacency list
of the graph is streamed in
some unknown order. There are also some problems that are very dependent
on the order of the stream (i.e., asymmetric functions), such as counting
the number of inversions in a stream and finding the longest increasing
subsequence.
These algorithms have many similarities with online algorithms since they both require decisions to be made before all data are available, but they are not identical. Data stream algorithms only have limited memory available but they may be able to defer action until a group of points arrive, while online algorithms are required to take action as soon as each point arrives.
If the algorithm is an approximation algorithm then the accuracy of the answer is another key factor. The accuracy is often stated as an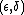 approximation meaning that the algorithm achieves an error of less than
approximation meaning that the algorithm achieves an error of less than  with probability
with probability  .
.
such as
monitoring network links for elephant flow
s, counting the number of
distinct flows, estimating the distribution of flow sizes, and so
on. They also have applications in
databases, such as estimating the size of a join
.
 th frequency moment of a set of frequencies
th frequency moment of a set of frequencies
 is defined as
is defined as  .
.
The first moment is simply the sum of the frequencies
is simply the sum of the frequencies
(i.e., the total count). The second moment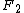 is useful for
is useful for
computing statistical properties of the data, such as the Gini coefficient
of variation. is defined as the frequency of the
is defined as the frequency of the
most frequent item(s).
The seminal paper of Alon, Matias, and Szegedy dealt with the
problem of estimating the frequency moments.
 whose frequency
whose frequency  , say. Some
, say. Some
notable algorithms are:
 moment) is another problem that has been well studied.
moment) is another problem that has been well studied.
The first algorithm for it was proposed by Flajolet and Martin, and the
best known algorithm is attributed to D. Kane, J. Nelson and D. Woodruff. It uses O(ε^2 + log d) space, with O(1) worst-case update and reporting times, as well as universal hash functions and a r-wise independent hash family where r = Ω(log(1/ε)/ log log(1/ε)) (so Ω(2.4) for 1% error) ..
 is
is
defined as , where
, where  .
.
Estimation of this quantity in a stream has been done by:
that have been studied. By far, the most common technique for computing
these lower bounds has been using communication complexity
.
Tutorials and surveys
Courses
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, streaming algorithms are algorithms for
processing data streams in which the input is presented as a sequence of
items and can be examined in only a few passes (typically just one). These
algorithms have limited memory available to them (much less than the input
size) and also limited processing time per item.
These constraints may mean that an algorithm produces an approximate answer based on a summary or "sketch" of the data stream in memory.
History
Though streaming algorithms had already been studied by Munro andPaterson as well as Flajolet and
Martin, the field of streaming
algorithms was first formalized and popularized in a paper by Noga Alon
Noga Alon
Noga Alon is an Israeli mathematician noted for his contributions to combinatorics and theoretical computer science, having authored hundreds of papers.- Academic background :...
,
Yossi Matias, and Mario Szegedy
Mario Szegedy
Mario Szegedy is a Hungarian computer scientist, professor of computer science at Rutgers University. He received his Ph.D. in computer science in 1989 from the University of Chicago...
.
For this paper, the authors later won the Gödel Prize
Gödel Prize
The Gödel Prize is a prize for outstanding papers in theoretical computer science, named after Kurt Gödel and awarded jointly by the European Association for Theoretical Computer Science and the Association for Computing Machinery Special Interest Group on Algorithms and Computation Theory .The...
in 2005 "for their foundational
contribution to streaming algorithms." There has since been a large body
of work centered around data streaming algorithms that spans a diverse
spectrum of computer science fields such as theory, databases, networking,
and natural language processing.
Models
In the data stream model, some or all of the input data that areto be operated on are not available for random access from disk or
memory, but rather arrive as one or more continuous data streams.
Streams can be denoted as an ordered sequence of points (or "updates") that must be accessed in order and can be read only once or a small number of times.
Much of the streaming literature is concerned with computing statistics on
frequency distributions that are too large to be stored. For this class of
problems, there is a vector

(initialized to the zero vector
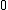 ) that has updates
) that has updatespresented to it in a stream. The goal of these algorithms is to compute
functions of
 using considerably less space than it
using considerably less space than itwould take to represent
 precisely. There are two
precisely. There are twocommon models for updating such streams, called the "cash register" and
"turnstile" models.
In the cash register model each update is of the form
 , so that
, so that  is incremented by some positive
is incremented by some positiveinteger
 . A notable special case is when
. A notable special case is when 
(only unit insertions are permitted).
In the turnstile model each update is of the form
 , so that
, so that 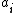 is incremented by some (possible
is incremented by some (possiblenegative) integer
 . In the "strict turnstile" model, no
. In the "strict turnstile" model, no at any time may be less than zero.
at any time may be less than zero.Several papers also consider the "sliding window" model. In this model,
the function of interest is computing over a fixed-size window in the
stream. As the stream progresses, items from the end of the window are
removed from consideration while new items from the stream take their
place.
Besides the above frequency-based problems, some other types of problems
have also been studied. Many graph problems are solved in the setting
where the adjacency matrix
Adjacency matrix
In mathematics and computer science, an adjacency matrix is a means of representing which vertices of a graph are adjacent to which other vertices...
or the adjacency list
Adjacency list
In graph theory, an adjacency list is the representation of all edges or arcs in a graph as a list.If the graph is undirected, every entry is a set of two nodes containing the two ends of the corresponding edge; if it is directed, every entry is a tuple of two nodes, one denoting the source node...
of the graph is streamed in
some unknown order. There are also some problems that are very dependent
on the order of the stream (i.e., asymmetric functions), such as counting
the number of inversions in a stream and finding the longest increasing
subsequence.
Evaluation
The performance of an algorithm that operates on data streams is measured by three basic factors:- The number of passes the algorithm must make over the stream.
- The available memory.
- The running time of the algorithm.
These algorithms have many similarities with online algorithms since they both require decisions to be made before all data are available, but they are not identical. Data stream algorithms only have limited memory available but they may be able to defer action until a group of points arrive, while online algorithms are required to take action as soon as each point arrives.
If the algorithm is an approximation algorithm then the accuracy of the answer is another key factor. The accuracy is often stated as an
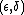 approximation meaning that the algorithm achieves an error of less than
approximation meaning that the algorithm achieves an error of less than  with probability
with probability  .
.Applications
Streaming algorithms have several applications in networkingComputer network
A computer network, often simply referred to as a network, is a collection of hardware components and computers interconnected by communication channels that allow sharing of resources and information....
such as
monitoring network links for elephant flow
Elephant Flow
In computer networking, an elephant flow is an extremely large continuous flow set up by a TCP flow measured over a network link. Elephant flows, though not numerous, can occupy a disproportionate share of the total bandwidth over a period of time...
s, counting the number of
distinct flows, estimating the distribution of flow sizes, and so
on. They also have applications in
databases, such as estimating the size of a join
Join (SQL)
An SQL join clause combines records from two or more tables in a database. It creates a set that can be saved as a table or used as is. A JOIN is a means for combining fields from two tables by using values common to each. ANSI standard SQL specifies four types of JOINs: INNER, OUTER, LEFT, and RIGHT...
.
Frequency moments
The th frequency moment of a set of frequencies
th frequency moment of a set of frequencies is defined as
is defined as  .
.The first moment
 is simply the sum of the frequencies
is simply the sum of the frequencies(i.e., the total count). The second moment
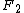 is useful for
is useful forcomputing statistical properties of the data, such as the Gini coefficient
Gini coefficient
The Gini coefficient is a measure of statistical dispersion developed by the Italian statistician and sociologist Corrado Gini and published in his 1912 paper "Variability and Mutability" ....
of variation.
 is defined as the frequency of the
is defined as the frequency of themost frequent item(s).
The seminal paper of Alon, Matias, and Szegedy dealt with the
problem of estimating the frequency moments.
Heavy hitters
Find all elements whose frequency
whose frequency  , say. Some
, say. Somenotable algorithms are:
- Karp-Papadimitriou-Shenker algorithm
- Count-Min sketchCount-Min sketchThe Count-Min sketch is a probabilistic sub-linear space streaming algorithm which can be used to summarize a data stream in many different ways. The algorithm was invented in 2003 by Graham Cormode and S...
- Sticky sampling
- Lossy counting
- Sample and Hold
- Multi-stage Bloom filters
- Count-sketch
- Sketch-guided sampling
Counting distinct elements
Counting the number of distinct elements in a stream (sometimes called the moment) is another problem that has been well studied.
moment) is another problem that has been well studied.The first algorithm for it was proposed by Flajolet and Martin, and the
best known algorithm is attributed to D. Kane, J. Nelson and D. Woodruff. It uses O(ε^2 + log d) space, with O(1) worst-case update and reporting times, as well as universal hash functions and a r-wise independent hash family where r = Ω(log(1/ε)/ log log(1/ε)) (so Ω(2.4) for 1% error) ..
Entropy
The (empirical) entropy of a set of frequencies is
isdefined as
 , where
, where  .
.Estimation of this quantity in a stream has been done by:
- McGregor et al.
- Do Ba et al.
- Lall et al.
- Chakraborty et al.
Lower bounds
Lower bounds have been computed for many of the data streaming problemsthat have been studied. By far, the most common technique for computing
these lower bounds has been using communication complexity
Communication complexity
The notion of communication complexity was introduced by Yao in 1979,who investigated the following problem involving two separated parties . Alice receives an n-bit string x and Bob another n-bit string y, and the goal is for one of them to compute a certain function f with the least amount of...
.
External links
- Princeton Lecture Notes
- Streaming Algorithms for Geometric Problems, by Piotr IndykPiotr IndykPiotr Indyk is an Associate Professor in the Theory of Computation Group at the Computer Science and Artificial Intelligence Laboratory, Massachusetts Institute of Technology.-Academic biography:...
, MIT - Dagstuhl Workshop on Sublinear Algorithms
- IIT Kanpur Workshop on Data Streaming
- List of open problems in streaming (compiled by Andrew McGregor) from discussion at the IITK Workshop on Algorithms for Data Streams, 2006.
- StreamIt - programming language and compilation infrastructure by MIT CSAIL
- IBM Spade - Stream Processing Application Declarative Engine
- IBM InfoSphere Streams
Tutorials and surveys
- Data Stream Algorithms and Applications by S. Muthu Muthukrishnan
- Stanford STREAM project survey
- Network Applications of Bloom filters, by Broder and Mitzenmacher
- Xu's SIGMETRICS 2007 tutorial
- Lecture notes from Data Streams course at Barbados in 2009, by Andrew McGregor and S. Muthu Muthukrishnan
Courses

