Stratonovich integral
Encyclopedia
In stochastic process
es, the Stratonovich integral (developed simultaneously by Ruslan L. Stratonovich
and D. L. Fisk) is a stochastic integral, the most common alternative to the Itō integral
. Although the Ito integral is the usual choice in applied mathematics, the Stratonovich integral is frequently used in physics.
In some circumstances, integrals in the Stratonovich definition are easier to manipulate. Unlike the Itō calculus
, Stratonovich integrals are defined such that the chain rule
of ordinary calculus holds.
Perhaps the most common situation in which these are encountered is as the solution to Stratonovich stochastic differential equation
s (SDE). These are equivalent to Itō SDEs and it is possible to convert between the two whenever one definition is more convenient.
, that is as a limit
of Riemann sum
s. Suppose that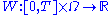
is a Wiener process
and
is a semimartingale
adapted
to the natural filtration
of the Wiener process. Then the Stratonovich integral
is defined to be the limit in probability of
as the mesh
of the partition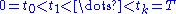
of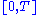 
tends to 0 (in the style of a Riemann–Stieltjes integral).
, the same procedure is used except for choosing the value of the process
at the left-hand endpoint of each subinterval: i.e.
in place of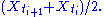 
Conversion between Itō and Stratonovich integrals may be performed using the formula
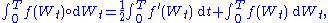
where ƒ is a continuously differentiable function and the last integral is an Itō integral .
It follows that if Xt is a time-homogeneous Itō diffusion with continuously differentiable diffusion coefficient σ (i.e. it satisfies the SDE
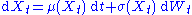), we have
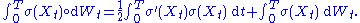
More generally, for any two semimartingale
s X and Y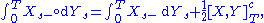
where
is the continuous part of the covariation
. With probability 1
, a general stochastic process
does not satisfy the criteria for convergence in the Riemann sense. If it did, then the Itō and Stratonovich definitions would converge to the same solution. As it is, for integrals with respect to Wiener processes, they are distinct.
an important topic in all uses of stochastic integrals. Various numerical approximations converge to the Stratonovich integral, making this important in numerical solutions of SDEs .
Note however that the most widely used Euler scheme for the numeric solution of
Langevin equation
s requires the equation to be in Itō form.
In many real-world applications, such as modelling stock prices, one only has information about past events, and hence the Itō interpretation is more natural. In financial mathematics the Itō interpretation is usually used.
In physics, however, stochastic integrals occur as the solutions of Langevin equation
s.
A Langevin equation is in fact a coarse-grained version of a more microscopic model; depending on the problem in consideration,
Stratonovich or Itō interpretation or even more exotic interpretations such as the isothermal interpretation,
are appropriate. The Stratonovich interpretation is the most frequently used interpretation within the physical sciences.
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
es, the Stratonovich integral (developed simultaneously by Ruslan L. Stratonovich
Ruslan L. Stratonovich
Ruslan Leont'evich Stratonovich was an outstanding physicist, engineer, and probabilist. Professor Stratonovich was born on May 31, 1930 in Moscow, Russia...
and D. L. Fisk) is a stochastic integral, the most common alternative to the Itō integral
Ito calculus
Itō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....
. Although the Ito integral is the usual choice in applied mathematics, the Stratonovich integral is frequently used in physics.
In some circumstances, integrals in the Stratonovich definition are easier to manipulate. Unlike the Itō calculus
Ito calculus
Itō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....
, Stratonovich integrals are defined such that the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
of ordinary calculus holds.
Perhaps the most common situation in which these are encountered is as the solution to Stratonovich stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
s (SDE). These are equivalent to Itō SDEs and it is possible to convert between the two whenever one definition is more convenient.
Definition
The Stratonovich integral can be defined in a manner similar to the Riemann integralRiemann integral
In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
, that is as a limit
Limit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
of Riemann sum
Riemann sum
In mathematics, a Riemann sum is a method for approximating the total area underneath a curve on a graph, otherwise known as an integral. It mayalso be used to define the integration operation. The method was named after German mathematician Bernhard Riemann....
s. Suppose that
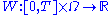is a Wiener processWiener process
In mathematics, the Wiener process is a continuous-time stochastic process named in honor of Norbert Wiener. It is often called standard Brownian motion, after Robert Brown...
and
is a semimartingaleSemimartingale
In probability theory, a real valued process X is called a semimartingale if it can be decomposed as the sum of a local martingale and an adapted finite-variation process....
adapted
Adapted process
In the study of stochastic processes, an adapted process is one that cannot "see into the future". An informal interpretation is that X is adapted if and only if, for every realisation and every n, Xn is known at time n...
to the natural filtration
Filtration (abstract algebra)
In mathematics, a filtration is an indexed set Si of subobjects of a given algebraic structure S, with the index i running over some index set I that is a totally ordered set, subject to the condition that if i ≤ j in I then Si ⊆ Sj...
of the Wiener process. Then the Stratonovich integral
is defined to be the limit in probability of
as the mesh
Partition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
of the partition
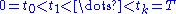of 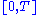tends to 0 (in the style of a Riemann–Stieltjes integral).Comparison with the Itō integral
In the definition of the Itō integralIto calculus
Itō calculus, named after Kiyoshi Itō, extends the methods of calculus to stochastic processes such as Brownian motion . It has important applications in mathematical finance and stochastic differential equations....
, the same procedure is used except for choosing the value of the process
at the left-hand endpoint of each subinterval: i.e. in place of 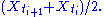Conversion between Itō and Stratonovich integrals may be performed using the formula
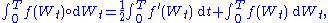
where ƒ is a continuously differentiable function and the last integral is an Itō integral .
It follows that if Xt is a time-homogeneous Itō diffusion with continuously differentiable diffusion coefficient σ (i.e. it satisfies the SDE
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
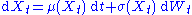), we have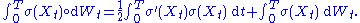More generally, for any two semimartingale
Semimartingale
In probability theory, a real valued process X is called a semimartingale if it can be decomposed as the sum of a local martingale and an adapted finite-variation process....
s X and Y
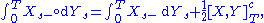
where
is the continuous part of the covariationQuadratic variation
In mathematics, quadratic variation is used in the analysis of stochastic processes such as Brownian motion and martingales. Quadratic variation is just one kind of variation of a process.- Definition :...
. With probability 1
Almost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
, a general stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
does not satisfy the criteria for convergence in the Riemann sense. If it did, then the Itō and Stratonovich definitions would converge to the same solution. As it is, for integrals with respect to Wiener processes, they are distinct.
Numerical methods
Stochastic integrals can rarely be solved in analytic form, making stochastic numerical integrationNumerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
an important topic in all uses of stochastic integrals. Various numerical approximations converge to the Stratonovich integral, making this important in numerical solutions of SDEs .
Note however that the most widely used Euler scheme for the numeric solution of
Langevin equation
Langevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
s requires the equation to be in Itō form.
Stratonovich integrals in real-world applications
The Stratonovich integral lacks the important property of the Itō integral, which does not "look into the future".In many real-world applications, such as modelling stock prices, one only has information about past events, and hence the Itō interpretation is more natural. In financial mathematics the Itō interpretation is usually used.
In physics, however, stochastic integrals occur as the solutions of Langevin equation
Langevin equation
In statistical physics, a Langevin equation is a stochastic differential equation describing the time evolution of a subset of the degrees of freedom. These degrees of freedom typically are collective variables changing only slowly in comparison to the other variables of the system...
s.
A Langevin equation is in fact a coarse-grained version of a more microscopic model; depending on the problem in consideration,
Stratonovich or Itō interpretation or even more exotic interpretations such as the isothermal interpretation,
are appropriate. The Stratonovich interpretation is the most frequently used interpretation within the physical sciences.