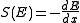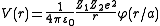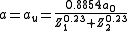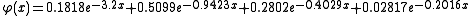.gif)
Stopping power (particle radiation)
Encyclopedia
In passing through matter, fast charged particles ionize
the atoms or molecules which they encounter. Thus, the fast particles gradually lose energy
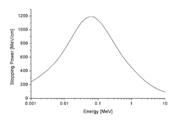
in many small steps. Stopping power is defined as the average energy loss of the particle per unit path length, measured for example in MeV
/cm (see figure to the right). Stopping power is a necessary ingredient for many parts of basic science, for medical and for technological applications.
pair (usually a positive ion and a (negative) electron) requires a fixed amount of energy (for example, 34 eV
in air), the density of ionisation along the path is proportional to the stopping power of the material.
Both electrons and positive ions lose energy while passing through matter. Positive ions are considered in most cases below.
'Stopping power' is treated as a property of the material, while 'energy loss per unit path length' describes what happens to the particle. However, numerical value and units are identical for both quantities; they are usually written with a minus sign in front:
where E means energy, and x is the path length. The minus sign makes S positive.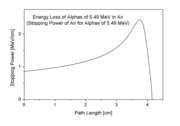 The stopping power and hence, the density of ionization, usually increases toward the end of range
The stopping power and hence, the density of ionization, usually increases toward the end of range
and reaches a maximum, the Bragg peak
, shortly before the energy drops to zero. The curve that describes this is called the Bragg curve. This is of great practical importance for radiation therapy
.
The equation above defines the linear stopping power which may be expressed in units like MeV
/mm or similar. Very often one divides S(E) by the density of the material to obtain the mass stopping power which may be expressed in units like MeV/(mg/cm2)(for total stopping power) or similar. The mass stopping power is nearly independent of the density of the material.
The picture shows how the stopping power of 5.49 MeV
alpha particles increases while the particle traverses air, until it reaches the maximum. This particular energy corresponds to that of the alpha particle radiation from naturally radioactive gas radon
(222Rn) which is present in the air in minute amounts wherever the ground contains granite.
The mean range can be calculated by integrating
the reciprocal stopping power over energy. The deposited energy can be obtained by integrating the stopping power over the entire path length of the ion when it moves in the solid.
Since the number of collisions an ion experiences with electrons is large, and since the charge state of the ion while traversing the medium may change frequently, it is very difficult to describe all possible interactions for all possible ion charge states. Instead, the electronic stopping power is often given as a simple function of energy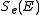 which is an average taken over all energy loss processes for different charge states. It can be theoretically determined to an accuracy of a few % in the energy range above several hundred keV per nucleon
which is an average taken over all energy loss processes for different charge states. It can be theoretically determined to an accuracy of a few % in the energy range above several hundred keV per nucleon
from theoretical treatments, the best known being the Bethe formula
. At energies lower than about 100 keV per nucleon, it becomes more difficult to determine the electronic stopping theoretically.
Graphical presentations of experimental values of the electronic stopping power for many ions in many substances have been given by Paul. The accuracy of various stopping tables has been determined using statistical comparisons.
 By nuclear stopping, one means elastic collisions between the ion and atoms in the sample (the established designation "nuclear" is a misnomer since nuclear stopping is not due to nuclear forces. If one knows the form of the repulsive potential
By nuclear stopping, one means elastic collisions between the ion and atoms in the sample (the established designation "nuclear" is a misnomer since nuclear stopping is not due to nuclear forces. If one knows the form of the repulsive potential 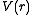 between two atoms (see below), it is possible to calculate the nuclear stopping power
between two atoms (see below), it is possible to calculate the nuclear stopping power 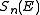 . In the stopping power figure shown above for protons in aluminum, nuclear stopping is negligible except at the lowest energy. Nuclear stopping increases when the mass of the ion increases. In the figure shown here, nuclear stopping is larger than electronic stopping at low energy. For very light ions slowing down in heavy materials, the nuclear stopping is weaker than the electronic at all energies.
. In the stopping power figure shown above for protons in aluminum, nuclear stopping is negligible except at the lowest energy. Nuclear stopping increases when the mass of the ion increases. In the figure shown here, nuclear stopping is larger than electronic stopping at low energy. For very light ions slowing down in heavy materials, the nuclear stopping is weaker than the electronic at all energies.
At not too high energies, the stopping power is therefore the sum of two terms: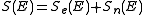 . Several semi-empirical stopping power formulas have been devised. The model given by Ziegler, Biersack and Littmark (the so called "ZBL" stopping), implemented in different versions of the TRIM/SRIM
. Several semi-empirical stopping power formulas have been devised. The model given by Ziegler, Biersack and Littmark (the so called "ZBL" stopping), implemented in different versions of the TRIM/SRIM
codes, is used most often today.
At even higher energies, one has to consider, in addition, radiative stopping power which is due to the emission of bremsstrahlung
in the electric fields of the nuclei of the material traversed.
Close to the surface, both nuclear and electronic stopping may lead to sputtering
.
),
nuclear reactions and (especially for electrons) bremsstrahlung
and Cherenkov radiation
contribute to the slowing down of all charged particles. The remainder of this article mainly deals with lower energies.
 In the beginning of the slowing-down process at high energies, the ion is slowed down mainly by electronic stopping, and it moves almost in a straight path. When the ion has slowed down sufficiently, the collisions with nuclei (the nuclear stopping) become more and more probable, finally dominating the slowing down. When atoms of the solid receive significant recoil energies when struck by the ion, they will be removed from their lattice
In the beginning of the slowing-down process at high energies, the ion is slowed down mainly by electronic stopping, and it moves almost in a straight path. When the ion has slowed down sufficiently, the collisions with nuclei (the nuclear stopping) become more and more probable, finally dominating the slowing down. When atoms of the solid receive significant recoil energies when struck by the ion, they will be removed from their lattice
positions, and produce a cascade of further collisions
in the material. These
collision cascade
s are the main cause of damage production during ion implantation in metals and semiconductors.
When the energies of all atoms in the system have fallen below the threshold displacement energy
, the production of new damage ceases, and the concept of nuclear stopping is no longer meaningful.
The total amount of energy deposited by the nuclear collisions to atoms in the materials is called the nuclear deposited energy.
The inset in the figure shows a typical range distribution of ions deposited in the solid. The case shown here might for instance be the slowing down of a 1 MeV silicon ion in silicon. The mean range for a 1 MeV ion is typically in the micrometer
range.
where φ(r) → 1 when r → 0. Here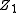 and
and 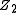 are the charges of the interacting nuclei, and r the distance between them; a is the so called screening parameter.
are the charges of the interacting nuclei, and r the distance between them; a is the so called screening parameter.
A large number of different repulsive potentials and screening functions have been proposed over the years, some determined semi-empirically, others from theoretical calculations. A much used repulsive potential is the one given by Ziegler, Biersack and Littmark, the so called ZBL repulsive potential. It has been constructed by fitting a universal screening function to theoretically obtained potentials calculated for a large variety of atom pairs. The ZBL screening parameter and function have the forms
and
where x = r/au, and a0 is the Bohr atomic radius = 0.529 Å.
The standard deviation of the fit of the universal ZBL repulsive potential to the theoretically calculated pair-specific potentials it is fit to is 18 % above 2 eV.
Even more accurate repulsive potentials can be obtained from self-consistent total energy calculations using density-functional theory and the local-density approximation
(LDA) for electronic exchange and correlation.
Conventional methods used to calculate ion ranges are based on the binary collision approximation
(BCA). In these methods the movement of ions in the implanted sample is treated as a succession of individual collisions between the recoil ion and atoms in the sample. For each individual collision the classical scattering integral is solved by numerical integration.
The impact parameter p in the scattering integral is determined either from a stochastic distribution or in a way that takes into account the crystal structure of the sample.
The former method is suitable only in simulations of implantation into amorphous materials,
as it does not account for channeling.
The best known BCA
simulation program is TRIM/SRIM
(acronym
for TRansport of Ions in Matter, in more recent versions
called Stopping and Range of Ions in Matter), which is based on the ZBL electronic stopping and interatomic potential. It has a very easy-to-use user interface,
and has default parameters for all ions in all materials up to an ion energy of 1 GeV,
which has made it immensely popular. However, it doesn't take account of the crystal structure, which severely limits its usefulness in many cases. Several BCA programs overcome this difficulty; some fairly well known are MARLOWE, BCCRYS and crystal-TRIM.
Although the BCA methods have been successfully used in describing many physical processes, they have some obstacles for describing the slowing down process of energetic ions realistically. Basic assumption that collisions are binary results in severe problems when trying to take multiple interactions into account. Also, in simulating crystalline materials the selection process of the next colliding lattice atom and the impact parameter p always involve several parameters which may not have perfectly well defined values, which may affect the results 10-20 % even for quite reasonable-seeming choices of the parameter values. The best reliability in BCA is obtained by including multiple collisions in the calculations, which is not easy to do correctly. However, at least MARLOWE does this.
A fundamentally more straightforward way to model multiple atomic collisions is provided by molecular dynamics
(MD) simulations, in which the time evolution of a system of atoms is calculated by solving the equations of motion numerically. Special MD methods have been devised in which the number of interactions and atoms involved in MD simulations have been reduced in order to make them efficient enough for calculating ion ranges.
When a fast charged particle passes through matter, it ionizes or excites the atoms or molecules that it encounters, losing energy in small steps. The mean rate at which it loses energy depends on the material, the kind of particle and also its momentum. In practical cases, most relativistic particles (e.g., cosmic-ray muon
s) are minimum ionizing particles.
Ionization
Ionization is the process of converting an atom or molecule into an ion by adding or removing charged particles such as electrons or other ions. This is often confused with dissociation. A substance may dissociate without necessarily producing ions. As an example, the molecules of table sugar...
the atoms or molecules which they encounter. Thus, the fast particles gradually lose energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
in many small steps. Stopping power is defined as the average energy loss of the particle per unit path length, measured for example in MeV
Electronvolt
In physics, the electron volt is a unit of energy equal to approximately joule . By definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt...
/cm (see figure to the right). Stopping power is a necessary ingredient for many parts of basic science, for medical and for technological applications.

Stopping power, Bragg curve and range
The stopping power depends on the type and energy of the particle and on the properties of the material it passes. Since the production of an ionIon
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
pair (usually a positive ion and a (negative) electron) requires a fixed amount of energy (for example, 34 eV
Electronvolt
In physics, the electron volt is a unit of energy equal to approximately joule . By definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt...
in air), the density of ionisation along the path is proportional to the stopping power of the material.
Both electrons and positive ions lose energy while passing through matter. Positive ions are considered in most cases below.
'Stopping power' is treated as a property of the material, while 'energy loss per unit path length' describes what happens to the particle. However, numerical value and units are identical for both quantities; they are usually written with a minus sign in front:
where E means energy, and x is the path length. The minus sign makes S positive.

Range (particle radiation)
In passing through matter, charged particles ionize and thus lose energy in many steps, until their energy is zero. The distance to this point is called the range of the particle...
and reaches a maximum, the Bragg peak
Bragg Peak
The Bragg peak is a pronounced peak on the Bragg curve which plots the energy loss of ionizing radiation during its travel through matter. For protons, α-rays, and other ion rays, the peak occurs immediately before the particles come to rest...
, shortly before the energy drops to zero. The curve that describes this is called the Bragg curve. This is of great practical importance for radiation therapy
Radiation therapy
Radiation therapy , radiation oncology, or radiotherapy , sometimes abbreviated to XRT or DXT, is the medical use of ionizing radiation, generally as part of cancer treatment to control malignant cells.Radiation therapy is commonly applied to the cancerous tumor because of its ability to control...
.
The equation above defines the linear stopping power which may be expressed in units like MeV
Electronvolt
In physics, the electron volt is a unit of energy equal to approximately joule . By definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt...
/mm or similar. Very often one divides S(E) by the density of the material to obtain the mass stopping power which may be expressed in units like MeV/(mg/cm2)(for total stopping power) or similar. The mass stopping power is nearly independent of the density of the material.
The picture shows how the stopping power of 5.49 MeV
Electronvolt
In physics, the electron volt is a unit of energy equal to approximately joule . By definition, it is equal to the amount of kinetic energy gained by a single unbound electron when it accelerates through an electric potential difference of one volt...
alpha particles increases while the particle traverses air, until it reaches the maximum. This particular energy corresponds to that of the alpha particle radiation from naturally radioactive gas radon
Radon
Radon is a chemical element with symbol Rn and atomic number 86. It is a radioactive, colorless, odorless, tasteless noble gas, occurring naturally as the decay product of uranium or thorium. Its most stable isotope, 222Rn, has a half-life of 3.8 days...
(222Rn) which is present in the air in minute amounts wherever the ground contains granite.
The mean range can be calculated by integrating
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
the reciprocal stopping power over energy. The deposited energy can be obtained by integrating the stopping power over the entire path length of the ion when it moves in the solid.
Electronic, nuclear and radiative stopping
By electronic stopping, one means slowing down due to the inelastic collisions between bound electrons in the medium and the ion moving through it. The term inelastic is used to signify that the collisions may result both in excitations of bound electrons of the medium, and in excitations of the electron cloud of the ion.Since the number of collisions an ion experiences with electrons is large, and since the charge state of the ion while traversing the medium may change frequently, it is very difficult to describe all possible interactions for all possible ion charge states. Instead, the electronic stopping power is often given as a simple function of energy
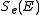 which is an average taken over all energy loss processes for different charge states. It can be theoretically determined to an accuracy of a few % in the energy range above several hundred keV per nucleon
which is an average taken over all energy loss processes for different charge states. It can be theoretically determined to an accuracy of a few % in the energy range above several hundred keV per nucleonNucleon
In physics, a nucleon is a collective name for two particles: the neutron and the proton. These are the two constituents of the atomic nucleus. Until the 1960s, the nucleons were thought to be elementary particles...
from theoretical treatments, the best known being the Bethe formula
Bethe formula
In nuclear physics and theoretical physics, charged particles moving through matter interact with the electrons of atoms in the material. The interaction excites or ionizes the atoms. This leads to an energy loss of the traveling particle...
. At energies lower than about 100 keV per nucleon, it becomes more difficult to determine the electronic stopping theoretically.
Graphical presentations of experimental values of the electronic stopping power for many ions in many substances have been given by Paul. The accuracy of various stopping tables has been determined using statistical comparisons.

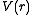 between two atoms (see below), it is possible to calculate the nuclear stopping power
between two atoms (see below), it is possible to calculate the nuclear stopping power 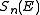 . In the stopping power figure shown above for protons in aluminum, nuclear stopping is negligible except at the lowest energy. Nuclear stopping increases when the mass of the ion increases. In the figure shown here, nuclear stopping is larger than electronic stopping at low energy. For very light ions slowing down in heavy materials, the nuclear stopping is weaker than the electronic at all energies.
. In the stopping power figure shown above for protons in aluminum, nuclear stopping is negligible except at the lowest energy. Nuclear stopping increases when the mass of the ion increases. In the figure shown here, nuclear stopping is larger than electronic stopping at low energy. For very light ions slowing down in heavy materials, the nuclear stopping is weaker than the electronic at all energies.At not too high energies, the stopping power is therefore the sum of two terms:
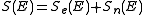 . Several semi-empirical stopping power formulas have been devised. The model given by Ziegler, Biersack and Littmark (the so called "ZBL" stopping), implemented in different versions of the TRIM/SRIM
. Several semi-empirical stopping power formulas have been devised. The model given by Ziegler, Biersack and Littmark (the so called "ZBL" stopping), implemented in different versions of the TRIM/SRIMStopping and Range of Ions in Matter
Stopping and Range of Ions in Matter is a group of computer programs which calculate interaction of ions with matter; the core of SRIM is a program Transport of ions in matter . The programs were developed by James F. Ziegler and Jochen P. Biersack around 1983 and are being continuously upgraded...
codes, is used most often today.
At even higher energies, one has to consider, in addition, radiative stopping power which is due to the emission of bremsstrahlung
Bremsstrahlung
Bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into a photon because energy is conserved. The term is...
in the electric fields of the nuclei of the material traversed.
Close to the surface, both nuclear and electronic stopping may lead to sputtering
Sputtering
Sputtering is a process whereby atoms are ejected from a solid target material due to bombardment of the target by energetic particles. It is commonly used for thin-film deposition, etching and analytical techniques .-Physics of sputtering:...
.
Energy regimes
At very high energies (larger than several hundreds of MeV per nucleonNucleon
In physics, a nucleon is a collective name for two particles: the neutron and the proton. These are the two constituents of the atomic nucleus. Until the 1960s, the nucleons were thought to be elementary particles...
),
nuclear reactions and (especially for electrons) bremsstrahlung
Bremsstrahlung
Bremsstrahlung is electromagnetic radiation produced by the deceleration of a charged particle when deflected by another charged particle, typically an electron by an atomic nucleus. The moving particle loses kinetic energy, which is converted into a photon because energy is conserved. The term is...
and Cherenkov radiation
Cherenkov radiation
Cherenkov radiation is electromagnetic radiation emitted when a charged particle passes through a dielectric medium at a speed greater than the phase velocity of light in that medium...
contribute to the slowing down of all charged particles. The remainder of this article mainly deals with lower energies.
The slowing-down process in solids

Crystal structure
In mineralogy and crystallography, crystal structure is a unique arrangement of atoms or molecules in a crystalline liquid or solid. A crystal structure is composed of a pattern, a set of atoms arranged in a particular way, and a lattice exhibiting long-range order and symmetry...
positions, and produce a cascade of further collisions
Collision cascade
A collision cascade is a set of nearby adjacent energetic collisions of atoms induced by an energetic particle in a solid or liquid....
in the material. These
collision cascade
Collision cascade
A collision cascade is a set of nearby adjacent energetic collisions of atoms induced by an energetic particle in a solid or liquid....
s are the main cause of damage production during ion implantation in metals and semiconductors.
When the energies of all atoms in the system have fallen below the threshold displacement energy
Threshold displacement energy
The threshold displacement energy T_d is the minimum kinetic energythat an atom in a solid needs to be permanentlydisplaced from its lattice site to adefect position.It is also known as "displacement threshold energy" or just "displacement energy"....
, the production of new damage ceases, and the concept of nuclear stopping is no longer meaningful.
The total amount of energy deposited by the nuclear collisions to atoms in the materials is called the nuclear deposited energy.
The inset in the figure shows a typical range distribution of ions deposited in the solid. The case shown here might for instance be the slowing down of a 1 MeV silicon ion in silicon. The mean range for a 1 MeV ion is typically in the micrometer
Micrometer
A micrometer , sometimes known as a micrometer screw gauge, is a device incorporating a calibrated screw used widely for precise measurement of small distances in mechanical engineering and machining as well as most mechanical trades, along with other metrological instruments such as dial, vernier,...
range.
Repulsive interatomic potentials
At very small distances between the nuclei the repulsive interaction can be regarded as essentially Coulombic. At greater distances, the electron clouds screen the nuclei from each other. Thus the repulsive potential can be described by multiplying the Coulombic repulsion between nuclei with a screening function φ(r/a),where φ(r) → 1 when r → 0. Here
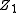 and
and 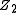 are the charges of the interacting nuclei, and r the distance between them; a is the so called screening parameter.
are the charges of the interacting nuclei, and r the distance between them; a is the so called screening parameter.A large number of different repulsive potentials and screening functions have been proposed over the years, some determined semi-empirically, others from theoretical calculations. A much used repulsive potential is the one given by Ziegler, Biersack and Littmark, the so called ZBL repulsive potential. It has been constructed by fitting a universal screening function to theoretically obtained potentials calculated for a large variety of atom pairs. The ZBL screening parameter and function have the forms
and
where x = r/au, and a0 is the Bohr atomic radius = 0.529 Å.
The standard deviation of the fit of the universal ZBL repulsive potential to the theoretically calculated pair-specific potentials it is fit to is 18 % above 2 eV.
Even more accurate repulsive potentials can be obtained from self-consistent total energy calculations using density-functional theory and the local-density approximation
Local-density approximation
Local-density approximations are a class of approximations to the exchange-correlation energy functional in density functional theory that depend solely upon the value of the electronic density at each point in space . Many approaches can yield local approximations to the XC energy...
(LDA) for electronic exchange and correlation.
Channeling
In crystalline materials the ion may in some instances get "channeled", i.e., get focused into a channel between crystal planes where it experiences almost no collisions with nuclei. Also, the electronic stopping power may be weaker in the channel. Thus the nuclear and electronic stopping do not only depend on material type and density but also on its microscopic structure and cross-section.Computer simulations of ion slowing down
Computer simulation methods to calculate the motion of ions in a medium have been developed since the 1960s, and are now the dominant way of treating stopping power theoretically. The basic idea in them is to follow the movement of the ion in the medium by simulating the collisions with nuclei in the medium. The electronic stopping power is usually taken into account as a frictional force slowing down the ion.Conventional methods used to calculate ion ranges are based on the binary collision approximation
Binary collision approximation
The binary collision approximation signifies a method used in ion irradiation physics to enable efficient computer simulation of the penetration depth and...
(BCA). In these methods the movement of ions in the implanted sample is treated as a succession of individual collisions between the recoil ion and atoms in the sample. For each individual collision the classical scattering integral is solved by numerical integration.
The impact parameter p in the scattering integral is determined either from a stochastic distribution or in a way that takes into account the crystal structure of the sample.
The former method is suitable only in simulations of implantation into amorphous materials,
as it does not account for channeling.
The best known BCA
Binary collision approximation
The binary collision approximation signifies a method used in ion irradiation physics to enable efficient computer simulation of the penetration depth and...
simulation program is TRIM/SRIM
Stopping and Range of Ions in Matter
Stopping and Range of Ions in Matter is a group of computer programs which calculate interaction of ions with matter; the core of SRIM is a program Transport of ions in matter . The programs were developed by James F. Ziegler and Jochen P. Biersack around 1983 and are being continuously upgraded...
(acronym
Acronym and initialism
Acronyms and initialisms are abbreviations formed from the initial components in a phrase or a word. These components may be individual letters or parts of words . There is no universal agreement on the precise definition of the various terms , nor on written usage...
for TRansport of Ions in Matter, in more recent versions
called Stopping and Range of Ions in Matter), which is based on the ZBL electronic stopping and interatomic potential. It has a very easy-to-use user interface,
and has default parameters for all ions in all materials up to an ion energy of 1 GeV,
which has made it immensely popular. However, it doesn't take account of the crystal structure, which severely limits its usefulness in many cases. Several BCA programs overcome this difficulty; some fairly well known are MARLOWE, BCCRYS and crystal-TRIM.
Although the BCA methods have been successfully used in describing many physical processes, they have some obstacles for describing the slowing down process of energetic ions realistically. Basic assumption that collisions are binary results in severe problems when trying to take multiple interactions into account. Also, in simulating crystalline materials the selection process of the next colliding lattice atom and the impact parameter p always involve several parameters which may not have perfectly well defined values, which may affect the results 10-20 % even for quite reasonable-seeming choices of the parameter values. The best reliability in BCA is obtained by including multiple collisions in the calculations, which is not easy to do correctly. However, at least MARLOWE does this.
A fundamentally more straightforward way to model multiple atomic collisions is provided by molecular dynamics
Molecular dynamics
Molecular dynamics is a computer simulation of physical movements of atoms and molecules. The atoms and molecules are allowed to interact for a period of time, giving a view of the motion of the atoms...
(MD) simulations, in which the time evolution of a system of atoms is calculated by solving the equations of motion numerically. Special MD methods have been devised in which the number of interactions and atoms involved in MD simulations have been reduced in order to make them efficient enough for calculating ion ranges.
Minimum ionizing particle
In physics, a minimum ionizing particle (or mip) is a particle whose mean energy loss rate through matter is close to the minimum.When a fast charged particle passes through matter, it ionizes or excites the atoms or molecules that it encounters, losing energy in small steps. The mean rate at which it loses energy depends on the material, the kind of particle and also its momentum. In practical cases, most relativistic particles (e.g., cosmic-ray muon
Muon
The muon |mu]] used to represent it) is an elementary particle similar to the electron, with a unitary negative electric charge and a spin of ½. Together with the electron, the tau, and the three neutrinos, it is classified as a lepton...
s) are minimum ionizing particles.
Further reading
- (Lindhard 1963) J. Lindhard, M. Scharff, and H. E. Shiøtt. Range concepts and heavy ion ranges. Mat. Fys. Medd. Dan. Vid. Selsk., 33(14):1, 1963.
- (Smith 1997) R. Smith (ed.), Atomic & ion collisions in solids and at surfaces: theory, simulation and applications, Cambridge University Press, Cambridge, UK, 1997,
External links
- The Energy Loss of charged particles passing through matter
- Stopping power and energy loss straggling calculations in solids by MELF-GOS model
- A Web-based module for Range and Stopping Power in Nucleonica
- Passage of charged particles through matter
- Stopping power for protons and alpha particles
- Stopping Power: Graphs and Data
- Penetration of charged particles through matter; lecture notes by E. Bonderup