Stokes line
Encyclopedia
In complex analysis
a Stokes line, named after Sir George Gabriel Stokes
, is a line in the complex plane
which 'turns on' different kinds of behaviour when one 'passes over' this line – although, somewhat confusingly, this definition is sometimes used for anti-Stokes lines. This article follows the former definition, more common in mathematical literature (but less common in physics literature). When approximating integral equations it is vital to know where the Stokes lines are so as to keep track of exponential smallness.
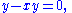
which it is often useful to approximate for many values of x – including complex values. If we regard the limit of x as large and real, and would like to approximate the Airy function for both positive and negative values, we would find that
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
a Stokes line, named after Sir George Gabriel Stokes
George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
, is a line in the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
which 'turns on' different kinds of behaviour when one 'passes over' this line – although, somewhat confusingly, this definition is sometimes used for anti-Stokes lines. This article follows the former definition, more common in mathematical literature (but less common in physics literature). When approximating integral equations it is vital to know where the Stokes lines are so as to keep track of exponential smallness.
The Airy function
The Airy function Ai(x) is one of two solutions to a simple differential equation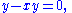which it is often useful to approximate for many values of x – including complex values. If we regard the limit of x as large and real, and would like to approximate the Airy function for both positive and negative values, we would find that
-
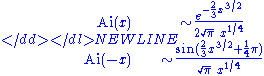
which are two very different expressions. What has happened is that as we have increased the argument of x from 0 to pi (rotating it around through the upper half complex plane) we have crossed a Stokes line, which in this case is at
. A more thorough analysis is possible by defining a new variable 
with small argument – we find that exponentially small terms are 'turned on' via the erf function. These small terms then grow, and cause the oscillatory behaviour at arg x = π.
Optics
In the context of optics, a Stokes line refers to the radiation of particular wavelengths present in the line spectra associated with fluorescence and the Raman scatteringRaman scatteringRaman scattering or the Raman effect is the inelastic scattering of a photon. It was discovered by Sir Chandrasekhara Venkata Raman and Kariamanickam Srinivasa Krishnan in liquids, and by Grigory Landsberg and Leonid Mandelstam in crystals....
. Stokes lines are of longer wavelength than that of the exciting radiation responsible for the fluorescence or Raman effect.
The energy of the scattered radiation is less than the incident radiation for the Stokes line and the energy of the scattered radiation is more than the incident radiation for the anti-Stokes line. The energy increase or decrease from the excitation is related to the vibrational energy spacing in the ground electronic state of the molecule and therefore the wavenumber of the Stokes and anti-Stokes lines are a direct measure of the vibrational energies of the molecule.