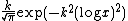Stieltjes–Wigert polynomials
Encyclopedia
In mathematics, Stieltjes–Wigert polynomials (named after T. J. Stieltjes and Carl Severin Wigert
) are family of basic hypergeometric orthogonal polynomials
in the basic Askey scheme
, for the weight function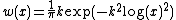
on the positive real line x > 0.
The moment problem for the Stieltjes–Wigert polynomials is indeterminate; in other words, there are many other measures giving the same family of orthogonal polynomials (see Krein's condition).
give a detailed list of their properties.
by
(where q = e–2k2).
Two examples of such weight functions are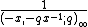
and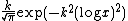
Carl Severin Wigert
Carl Severin Wigert was a Swedish mathematician who introduced Stieltjes–Wigert polynomials and worked on the divisor function....
) are family of basic hypergeometric orthogonal polynomials
Orthogonal polynomials
In mathematics, the classical orthogonal polynomials are the most widely used orthogonal polynomials, and consist of the Hermite polynomials, the Laguerre polynomials, the Jacobi polynomials together with their special cases the ultraspherical polynomials, the Chebyshev polynomials, and the...
in the basic Askey scheme
Askey scheme
In mathematics, the Askey scheme is a way of organizing orthogonal polynomials of hypergeometric or basic hypergeometric type into a hierarchy. For the classical orthogonal polynomials discussed in , the Askey scheme was first drawn by and by , and has since been extended by and to cover basic...
, for the weight function
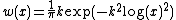
on the positive real line x > 0.
The moment problem for the Stieltjes–Wigert polynomials is indeterminate; in other words, there are many other measures giving the same family of orthogonal polynomials (see Krein's condition).
give a detailed list of their properties.
Definition
The polynomials are given in terms of basic hypergeometric functions and the Pochhammer symbolPochhammer symbol
In mathematics, the Pochhammer symbol introduced by Leo August Pochhammer is the notation ', where is a non-negative integer. Depending on the context the Pochhammer symbol may represent either the rising factorial or the falling factorial as defined below. Care needs to be taken to check which...
by

(where q = e–2k2).
Orthogonality
Since the moment problem for these polynomials is indeterminate there are many different weight functions on [0,∞] for which they are orthogonal.Two examples of such weight functions are
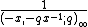
and