Stewart-Walker lemma
Encyclopedia
The Stewart–Walker lemma provides necessary and sufficient conditions for the linear
perturbation of a tensor
field to be gauge
-invariant.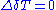
if and only if
one of the following holds
1.
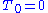
2.
is a constant scalar field
3.
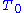is a linear combination of products of delta functions 
with 
has metric
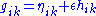. These manifolds can be put together to form a 5-manifold 
. A smooth curve 
can be constructed through 
with tangent 5-vector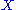 
, transverse to 
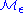. If 
is defined so that if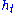 
is the family of 1-parameter maps which map 
and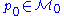 
then a point 
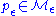can be written as 
. This also defines a pull back 
that maps a tensor field 
back onto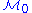 
. Given sufficient smoothness a Taylor expansion can be defined
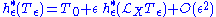
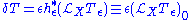is the linear perturbation of 
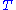. However, since the choice of 
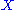is dependent on the choice of gauge
another gauge can be taken. Therefore the differences in gauge become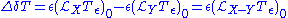
. Picking a chart where 
and 
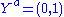then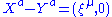 
which is a well defined vector in any 
and gives the result
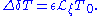
The only three possible ways this can be satisfied are those of the lemma.
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
perturbation of a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
field to be gauge
Gauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
-invariant.
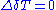if and only ifIf and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
one of the following holds
1.
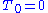
2.
is a constant scalar field3.
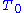is a linear combination of products of delta functions Derivation
A 1-parameter family of manifolds denoted by with has metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
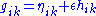. These manifolds can be put together to form a 5-manifold . A smooth curve can be constructed through with tangent 5-vector 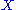, transverse to 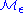. If is defined so that if 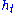is the family of 1-parameter maps which map and 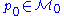then a point 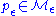can be written as . This also defines a pull back that maps a tensor field back onto 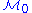. Given sufficient smoothness a Taylor expansion can be defined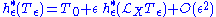 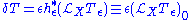is the linear perturbation of 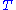. However, since the choice of 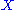is dependent on the choice of gaugeGauge theory
In physics, gauge invariance is the property of a field theory in which different configurations of the underlying fundamental but unobservable fields result in identical observable quantities. A theory with such a property is called a gauge theory...
another gauge can be taken. Therefore the differences in gauge become
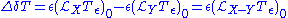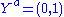. Picking a chart where and then 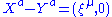which is a well defined vector in any and gives the result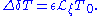The only three possible ways this can be satisfied are those of the lemma.