Stengle's Positivstellensatz
Encyclopedia
In real
semialgebraic geometry
, Stengle's Positivstellensatz (German
: "positive-locus-theorem" – see Satz
) characterizes polynomial
s that are positive on a semialgebraic set
, which is defined by systems of inequalities of polynomials with real
coefficients, or more generally, coefficients from any real-closed field.
It can be thought of as an ordered analogue of Hilbert's Nullstellensatz
. It was discovered by Gilbert Stengle.
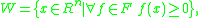
and let C be the cone generated by F (i.e., the subsemiring
of R[X1,…,Xn] generated by F and arbitrary squares). Let p ∈ R[X1,…,Xn] be a polynomial. Then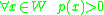
if and only if 
.
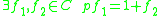The weak Positivstellensatz is the following variant of the Positivstellensatz. Let R be a real-closed field, and F, G, and H finite subsets of R[X1,…,Xn]. Let C be the cone generated by F, and I the ideal generated by G. Then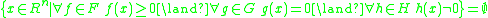
if and only if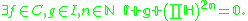
(Unlike Nullstellensatz, the "weak" form actually includes the "strong" form as a special case, so the terminology is a misnomer.)
Real algebraic geometry
In mathematics, real algebraic geometry is the study of real algebraic sets, i.e. real-number solutions to algebraic equations with real-number coefficients, and mappings between them ....
semialgebraic geometry
Semialgebraic set
In mathematics, a semialgebraic set is a subset S of Rn for some real closed field R defined by a finite sequence of polynomial equations and inequalities , or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph...
, Stengle's Positivstellensatz (German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
: "positive-locus-theorem" – see Satz
Satz (disambiguation)
Satz is a German word and name, and may refer to:* Satz, a formal section in music analysis* "theorem" in German, conventionally used in the name of certain theorems. Note however that the word "Theorem" is also used in German, generally for more important results, and thus in a stricter...
) characterizes polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
s that are positive on a semialgebraic set
Semialgebraic set
In mathematics, a semialgebraic set is a subset S of Rn for some real closed field R defined by a finite sequence of polynomial equations and inequalities , or any finite union of such sets. A semialgebraic function is a function with semialgebraic graph...
, which is defined by systems of inequalities of polynomials with real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
coefficients, or more generally, coefficients from any real-closed field.
It can be thought of as an ordered analogue of Hilbert's Nullstellensatz
Hilbert's Nullstellensatz
Hilbert's Nullstellensatz is a theorem which establishes a fundamental relationship between geometry and algebra. This relationship is the basis of algebraic geometry, an important branch of mathematics. It relates algebraic sets to ideals in polynomial rings over algebraically closed fields...
. It was discovered by Gilbert Stengle.
Statement
Let R be a real-closed field, and F a finite set of polynomials over R in n variables. Let W be the semialgebraic set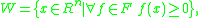and let C be the cone generated by F (i.e., the subsemiring
Semiring
In abstract algebra, a semiring is an algebraic structure similar to a ring, but without the requirement that each element must have an additive inverse...
of R[X1,…,Xn] generated by F and arbitrary squares). Let p ∈ R[X1,…,Xn] be a polynomial. Then
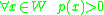if and only if 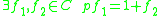.The weak Positivstellensatz is the following variant of the Positivstellensatz. Let R be a real-closed field, and F, G, and H finite subsets of R[X1,…,Xn]. Let C be the cone generated by F, and I the ideal generated by G. Then
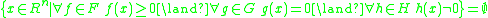
if and only if
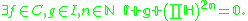
(Unlike Nullstellensatz, the "weak" form actually includes the "strong" form as a special case, so the terminology is a misnomer.)