Steinhaus theorem
Encyclopedia
Steinhaus theorem is a theorem
in real analysis
, first proved by H. Steinhaus, concerning the difference set of a set of positive measure
.
The theorem states that if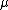 is a translation-invariant regular measure
is a translation-invariant regular measure
defined on the Borel set
s of the real line
, and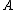 is a Borel measurable set with
is a Borel measurable set with 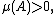 then the difference set
then the difference set
contains an open
neighborhood of the origin. Here, a measure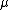 is called translation-invariant if
is called translation-invariant if

for all real numbers and all Borel measurable sets
and all Borel measurable sets 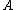 , where
, where 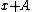 is the set of all points of the form
is the set of all points of the form  with
with  in
in 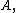 that is,
that is, 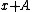 is obtained by shifting
is obtained by shifting 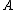 to the right by
to the right by  .
.
The theorem extends easily to any Borel-measurable set of positive measure in a locally compact group
.
Analogous theorem for nonmeagre
sets with Baire property also holds, and is sometimes called Steinhaus theorem, proof of which is almost identical to the one below.
If is a regular measure and
is a regular measure and 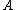 is a measurable set with positive finite measure
is a measurable set with positive finite measure 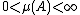 , then for every
, then for every 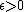 there are a compact set
there are a compact set 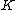 and an open set
and an open set 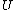 such that
such that
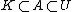 and
and 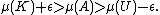
For our purpose it is enough to choose and
and 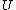 such that
such that 
Since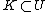 , there is an open cover of
, there is an open cover of  that is contained in
that is contained in 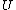 .
.  is compact, hence one can choose a small neighborhood
is compact, hence one can choose a small neighborhood 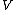 of
of  such that
such that 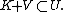
Let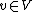 and suppose
and suppose  Then,
Then,
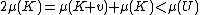
contradicting our choice of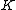 and
and  . Hence for all
. Hence for all 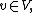 there exist
there exist 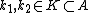 such that
such that 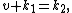
which means that . Q.E.D.
. Q.E.D.
Theorem
In mathematics, a theorem is a statement that has been proven on the basis of previously established statements, such as other theorems, and previously accepted statements, such as axioms...
in real analysis
Real analysis
Real analysis, is a branch of mathematical analysis dealing with the set of real numbers and functions of a real variable. In particular, it deals with the analytic properties of real functions and sequences, including convergence and limits of sequences of real numbers, the calculus of the real...
, first proved by H. Steinhaus, concerning the difference set of a set of positive measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
.
The theorem states that if
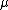 is a translation-invariant regular measure
is a translation-invariant regular measureRegular measure
In mathematics, a regular measure on a topological space is a measure for which every measurable set is "approximately open" and "approximately closed".-Definition:...
defined on the Borel set
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
s of the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, and
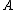 is a Borel measurable set with
is a Borel measurable set with 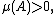 then the difference set
then the difference setcontains an open
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
neighborhood of the origin. Here, a measure
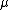 is called translation-invariant if
is called translation-invariant if
for all real numbers
 and all Borel measurable sets
and all Borel measurable sets 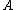 , where
, where 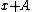 is the set of all points of the form
is the set of all points of the form  with
with  in
in 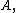 that is,
that is, 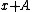 is obtained by shifting
is obtained by shifting 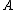 to the right by
to the right by  .
.The theorem extends easily to any Borel-measurable set of positive measure in a locally compact group
Locally compact group
In mathematics, a locally compact group is a topological group G which is locally compact as a topological space. Locally compact groups are important because they have a natural measure called the Haar measure. This allows one to define integrals of functions on G.Many of the results of finite...
.
Analogous theorem for nonmeagre
Meagre set
In the mathematical fields of general topology and descriptive set theory, a meagre set is a set that, considered as a subset of a topological space, is in a precise sense small or negligible...
sets with Baire property also holds, and is sometimes called Steinhaus theorem, proof of which is almost identical to the one below.
Proof
The following is a simple proof due to Karl Stromberghttp://www.jstor.org/sici?sici=0002-9939(197211)36%3A1%3C308%3ASNAEPO%3E2.0.CO%3B2-L.If
 is a regular measure and
is a regular measure and 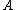 is a measurable set with positive finite measure
is a measurable set with positive finite measure 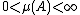 , then for every
, then for every 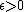 there are a compact set
there are a compact set 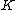 and an open set
and an open set 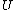 such that
such that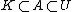 and
and 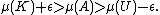
For our purpose it is enough to choose
 and
and 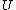 such that
such that 
Since
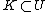 , there is an open cover of
, there is an open cover of  that is contained in
that is contained in 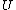 .
.  is compact, hence one can choose a small neighborhood
is compact, hence one can choose a small neighborhood 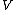 of
of  such that
such that 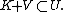
Let
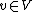 and suppose
and suppose  Then,
Then,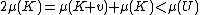
contradicting our choice of
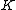 and
and  . Hence for all
. Hence for all 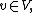 there exist
there exist 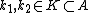 such that
such that 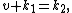
which means that
 . Q.E.D.
. Q.E.D.Q.E.D.
Q.E.D. is an initialism of the Latin phrase , which translates as "which was to be demonstrated". The phrase is traditionally placed in its abbreviated form at the end of a mathematical proof or philosophical argument when what was specified in the enunciation — and in the setting-out —...