
Stein's unbiased risk estimate
Encyclopedia
In statistics
, Stein's unbiased risk estimate (SURE) is an unbiased
estimator
of the mean-squared error of "a nearly arbitrary, nonlinear biased estimator." In other words, it provides an indication of the accuracy of a given estimator. This is important since the true mean-squared error of an estimator is a function of the unknown parameter to be estimated, and thus cannot be determined exactly.
The technique is named after its discoverer, Charles Stein.
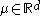 be an unknown parameter and let
be an unknown parameter and let 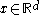 be a measurement vector which is distributed normally with mean
be a measurement vector which is distributed normally with mean 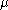 and covariance
and covariance 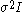 . Suppose
. Suppose 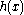 is an estimator of
is an estimator of 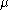 from
from  , and can be written
, and can be written  , where
, where 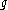 is weakly differentiable
is weakly differentiable
. Then, Stein's unbiased risk estimate is given by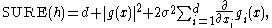
where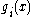 is the
is the 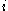 th component of the function
th component of the function 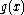 , and
, and  is the Euclidean norm.
is the Euclidean norm.
The importance of SURE is that it is an unbiased estimate of the mean-squared error (or squared error risk) of , i.e.
, i.e.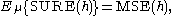
with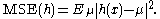
Thus, minimizing SURE can act as a surrogate for minimizing the MSE. Note that there is no dependence on the unknown parameter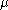 in the expression for SURE above. Thus, it can be manipulated (e.g., to determine optimal estimation settings) without knowledge of
in the expression for SURE above. Thus, it can be manipulated (e.g., to determine optimal estimation settings) without knowledge of  .
.
and Johnstone to determine the optimal shrinkage factor in a wavelet
denoising setting.
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, Stein's unbiased risk estimate (SURE) is an unbiased
Bias of an estimator
In statistics, bias of an estimator is the difference between this estimator's expected value and the true value of the parameter being estimated. An estimator or decision rule with zero bias is called unbiased. Otherwise the estimator is said to be biased.In ordinary English, the term bias is...
estimator
Estimator
In statistics, an estimator is a rule for calculating an estimate of a given quantity based on observed data: thus the rule and its result are distinguished....
of the mean-squared error of "a nearly arbitrary, nonlinear biased estimator." In other words, it provides an indication of the accuracy of a given estimator. This is important since the true mean-squared error of an estimator is a function of the unknown parameter to be estimated, and thus cannot be determined exactly.
The technique is named after its discoverer, Charles Stein.
Formal statement
Let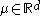 be an unknown parameter and let
be an unknown parameter and let 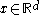 be a measurement vector which is distributed normally with mean
be a measurement vector which is distributed normally with mean 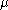 and covariance
and covariance 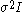 . Suppose
. Suppose 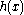 is an estimator of
is an estimator of 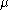 from
from  , and can be written
, and can be written  , where
, where 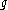 is weakly differentiable
is weakly differentiableWeak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
. Then, Stein's unbiased risk estimate is given by
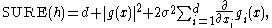
where
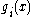 is the
is the 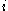 th component of the function
th component of the function 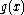 , and
, and  is the Euclidean norm.
is the Euclidean norm.The importance of SURE is that it is an unbiased estimate of the mean-squared error (or squared error risk) of
 , i.e.
, i.e.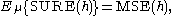
with
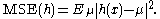
Thus, minimizing SURE can act as a surrogate for minimizing the MSE. Note that there is no dependence on the unknown parameter
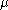 in the expression for SURE above. Thus, it can be manipulated (e.g., to determine optimal estimation settings) without knowledge of
in the expression for SURE above. Thus, it can be manipulated (e.g., to determine optimal estimation settings) without knowledge of  .
.Applications
A standard application of SURE is to choose a parametric form for an estimator, and then optimize the values of the parameters to minimize the risk estimate. This technique has been applied in several settings. For example, a variant of the James–Stein estimator can be derived by finding the optimal shrinkage estimator. The technique has also been used by DonohoDavid Donoho
David Leigh Donoho, born on March 5, 1957 in Los Angeles, is a professor of statistics at Stanford University, where he is also the Anne T. and Robert M. Bass Professor in the Humanities and Sciences...
and Johnstone to determine the optimal shrinkage factor in a wavelet
Wavelet
A wavelet is a wave-like oscillation with an amplitude that starts out at zero, increases, and then decreases back to zero. It can typically be visualized as a "brief oscillation" like one might see recorded by a seismograph or heart monitor. Generally, wavelets are purposefully crafted to have...
denoising setting.

