Static single assignment form
Encyclopedia
In compiler
design, static single assignment form (often abbreviated as SSA form or simply SSA) is a property of an intermediate representation (IR), which says that each variable is assigned exactly once. Existing variables in the original IR are split into versions, new variables typically indicated by the original name with a subscript in textbooks, so that every definition gets its own version. In SSA form, use-def chains
are explicit and each contains a single element.
SSA was developed by Ron Cytron, Jeanne Ferrante
, Barry K. Rosen, Mark N. Wegman, and F. Kenneth Zadeck, researchers at IBM in the 1980s.
In functional language compilers, such as those for Scheme, ML
and Haskell
, continuation-passing style
(CPS) is generally used while one might expect to find SSA in a compiler for Fortran
or C
. SSA is formally equivalent to a well-behaved subset of CPS (excluding non-local control flow, which does not occur when CPS is used as intermediate representation), so optimizations and transformations formulated in terms of one immediately apply to the other.
s, by simplifying the properties of variables. For example, consider this piece of code:
y := 1
y := 2
x := y
Humans can see that the first assignment is not necessary, and that the value of
to determine this. But if the program is in SSA form, both of these are immediate:
y1 := 1
y2 := 2
x1 := y2
Compiler optimization
algorithms which are either enabled or strongly enhanced by the use of SSA include:
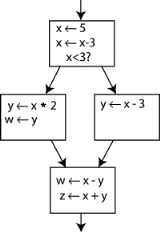
that point. For example, consider the following control flow graph
:
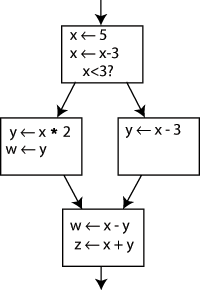
Notice that we could change the name on the left side of "x x - 3", and change the following uses of x to use that new name, and the program would still do the same thing. We exploit this in SSA by creating two new variables, x1 and x2, each of which is assigned only once. We likewise give distinguishing subscripts to all the other variables, and we get this:
x - 3", and change the following uses of x to use that new name, and the program would still do the same thing. We exploit this in SSA by creating two new variables, x1 and x2, each of which is assigned only once. We likewise give distinguishing subscripts to all the other variables, and we get this:
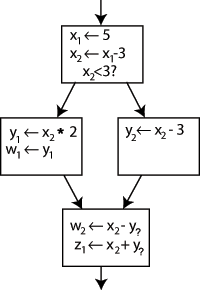
We've figured out which definition each use is referring to, except for one thing: the uses of y in the bottom block could be referring to either y1 or y2, depending on which way the control flow came from. So how do we know which one to use?
The answer is that we add a special statement, called a Φ (Phi) function, to the beginning of the last block. This statement will generate a new definition of y, y3, by "choosing" either y1 or y2, depending on which arrow control arrived from:
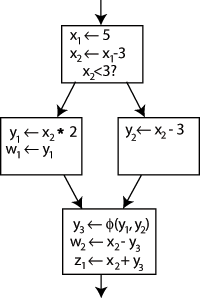
Now, the uses of y in the last block can simply use y3, and they'll obtain the correct value either way. You might ask at this point, do we need to add a Φ function for x too? The answer is no; only one version of x, namely x2 is reaching this place, so there's no problem.
A more general question along the same lines is, given an arbitrary control flow graph, how can I tell where to insert Φ functions, and for what variables? This is a difficult question, but one that has an efficient solution that can be computed using a concept called dominance frontiers.
Note: the Φ functions are not actually implemented; instead, they're just markers for the compiler to place the value of all the variables, which are grouped together by the Φ function, in the same location in memory (or same register).
According to Kenny Zadeck Φ functions were originally known as phoney functions while SSA was being developed at IBM Research in the 1980s. The formal name of Φ function was only adopted when the work was first published in an academic paper.
Now we can define the dominance frontier: a node B is in the dominance frontier of a node A if A does not strictly dominate B, but does dominate some immediate predecessor of B (possibly node A is the immediate predecessor of B. Then, because any node dominates itself and node A dominates itself, node B is in the dominance frontier of node A.). From A's point of view, these are the nodes at which other control paths, which don't go through A, make their earliest appearance.
Dominance frontiers capture the precise places at which we need Φ functions: if the node A defines a certain variable, then that definition and that definition alone (or redefinitions) will reach every node A dominates. Only when we leave these nodes and enter the dominance frontier must we account for other flows bringing in other definitions of the same variable. Moreover, no other Φ functions are needed in the control flow graph to deal with A's definitions, and we can do with no less.
One algorithm for computing the dominance frontier set is:
for each node b
if the number of immediate predecessors of b ≥ 2
for each p in immediate predecessors of b
runner := p
while runner ≠ doms(b)
add b to runner’s dominance frontier set
runner := doms(runner)
Note: in the code above, an immediate predecessor of node n is any node from which control is transferred to node n, and doms(b) is the node that immediately dominates node b (a singleton set).
There is an efficient algorithm for finding dominance frontiers of each node. This algorithm was originally described in Cytron et al. 1991. Also useful is chapter 19 of the book "Modern compiler implementation in Java" by Andrew Appel (Cambridge University Press, 2002). See the paper for more details.
Keith D. Cooper, Timothy J. Harvey, and Ken Kennedy of Rice University
describe an algorithm in their paper titled A Simple, Fast Dominance Algorithm. The algorithm uses well-engineered data structures to improve performance.
However, some of these Φ functions could be dead
. For this reason, minimal SSA does not necessarily produce the fewest number of Φ functions that are needed by a specific procedure. For some types of analysis, these Φ functions are superfluous and can cause the analysis to run less efficiently.
Construction of pruned SSA form uses live variable information
in the Φ function insertion phase to decide whether a given Φ function is needed. If the original variable name isn't live at the Φ function insertion point, the Φ function isn't inserted.
Another possibility is to treat pruning as a dead code elimination
problem. Then, a Φ function is live only if any use in the input program will be rewritten to it, or if it will be used as an argument in another Φ function. When entering SSA form, each use is rewritten to the nearest definition that dominates it. A Φ function will then be considered live as long as it is the nearest definition that dominates at least one use, or at least one argument of a live Φ.
Computing the set of block-local variables is a simpler and faster procedure than full live variable analysis, making semi-pruned SSA form more efficient to compute than pruned SSA form. On the other hand, semi-pruned SSA form will contain more Φ functions.
Performing optimizations on SSA form usually leads to entangled SSA-Webs, meaning there are phi instructions whose operands do not all have the same root operand. In such cases color-out algorithms are used to come out of SSA. Naive algorithms introduce a copy along each predecessor path which caused a source of different root symbol to be put in phi than the destination of phi. There are multiple algorithms for coming out of SSA with fewer copies, most use interference graphs or some approximation of it to do copy coalescing.
Renaming scheme extensions alter the renaming criterion. Recall that SSA form renames each variable when it is assigned a value. Alternative schemes include static single use form (which renames each variable at each statement when it is used) and static single information form (which renames each variable when it is assigned a value, and at the post-dominance frontier).
Feature-specific extensions retain the single assignment property for variables, but incorporate new semantics to model additional features. Some feature-specific extensions model high-level programming language features like arrays, objects and aliased pointers. Other feature-specific extensions model low-level architectural features like speculation and predication.
(ISBN 0-521-82060-X 2002) and C
(ISBN 0-521-60765-5, 199 8) versions.
Compiler
A compiler is a computer program that transforms source code written in a programming language into another computer language...
design, static single assignment form (often abbreviated as SSA form or simply SSA) is a property of an intermediate representation (IR), which says that each variable is assigned exactly once. Existing variables in the original IR are split into versions, new variables typically indicated by the original name with a subscript in textbooks, so that every definition gets its own version. In SSA form, use-def chains
Use-define chain
A Use-Definition Chain is a data structure that consists of a use, U, of a variable, and all the definitions, D, of that variable that can reach that use without any other intervening definitions...
are explicit and each contains a single element.
SSA was developed by Ron Cytron, Jeanne Ferrante
Jeanne Ferrante
Jeanne Ferrante is a computer scientist active in the field of compiler technology, where she has made important contributions regarding optimization and parallelization....
, Barry K. Rosen, Mark N. Wegman, and F. Kenneth Zadeck, researchers at IBM in the 1980s.
In functional language compilers, such as those for Scheme, ML
ML programming language
ML is a general-purpose functional programming language developed by Robin Milner and others in the early 1970s at the University of Edinburgh, whose syntax is inspired by ISWIM...
and Haskell
Haskell (programming language)
Haskell is a standardized, general-purpose purely functional programming language, with non-strict semantics and strong static typing. It is named after logician Haskell Curry. In Haskell, "a function is a first-class citizen" of the programming language. As a functional programming language, the...
, continuation-passing style
Continuation-passing style
In functional programming, continuation-passing style is a style of programming in which control is passed explicitly in the form of a continuation. Gerald Jay Sussman and Guy L. Steele, Jr...
(CPS) is generally used while one might expect to find SSA in a compiler for Fortran
Fortran
Fortran is a general-purpose, procedural, imperative programming language that is especially suited to numeric computation and scientific computing...
or C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
. SSA is formally equivalent to a well-behaved subset of CPS (excluding non-local control flow, which does not occur when CPS is used as intermediate representation), so optimizations and transformations formulated in terms of one immediately apply to the other.
Benefits
The primary usefulness of SSA comes from how it simultaneously simplifies and improves the results of a variety of compiler optimizationCompiler optimization
Compiler optimization is the process of tuning the output of a compiler to minimize or maximize some attributes of an executable computer program. The most common requirement is to minimize the time taken to execute a program; a less common one is to minimize the amount of memory occupied...
s, by simplifying the properties of variables. For example, consider this piece of code:
y := 1
y := 2
x := y
Humans can see that the first assignment is not necessary, and that the value of
y being used in the third line comes from the second assignment of y. A program would have to perform reaching definition analysisReaching definition
In compiler theory, a reaching definition for a given instruction is another instruction, the target variable of which may reach the given instruction without an intervening assignment. For example, in the following code: d1 : y := 3 d2 : x := y...
to determine this. But if the program is in SSA form, both of these are immediate:
y1 := 1
y2 := 2
x1 := y2
Compiler optimization
Compiler optimization
Compiler optimization is the process of tuning the output of a compiler to minimize or maximize some attributes of an executable computer program. The most common requirement is to minimize the time taken to execute a program; a less common one is to minimize the amount of memory occupied...
algorithms which are either enabled or strongly enhanced by the use of SSA include:
- constant propagation
- sparse conditional constant propagationSparse conditional constant propagationIn computer science, sparse conditional constant propagation is an optimization frequently applied in compilers after conversion to static single assignment form . It simultaneously removes some kinds of dead code and propagates constants throughout a program...
- dead code eliminationDead code eliminationIn compiler theory, dead code elimination is a compiler optimization to remove code which does not affect the program results. Removing such code has two benefits: it shrinks program size, an important...
- global value numberingGlobal value numberingGlobal value numbering is a compiler optimization based on the SSA intermediate representation. It sometimes helps eliminate redundant code that common subexpression elimination does not. At the same time, however, CSE may eliminate code that GVN does not, so both are often found in modern...
- partial redundancy eliminationPartial redundancy eliminationIn compiler theory, partial redundancy elimination is a compiler optimization that eliminates expressions that are redundant on some but not necessarily all paths through a program...
- strength reductionStrength reductionStrength reduction is a compiler optimization where expensive operations are replaced with equivalent but less expensive operations. The classic example of strength reduction converts "strong" multiplications inside a loop into "weaker" additions – something that frequently occurs in array...
- register allocationRegister allocationIn compiler optimization, register allocation is the process of assigning a large number of target program variables onto a small number of CPU registers...
Converting to SSA
Converting ordinary code into SSA form is primarily a simple matter of replacing the target of each assignment with a new variable, and replacing each use of a variable with the "version" of the variable reachingReaching definition
In compiler theory, a reaching definition for a given instruction is another instruction, the target variable of which may reach the given instruction without an intervening assignment. For example, in the following code: d1 : y := 3 d2 : x := y...
that point. For example, consider the following control flow graph
Control flow graph
A control flow graph in computer science is a representation, using graph notation, of all paths that might be traversed through a program during its execution.- Overview :...
:

Notice that we could change the name on the left side of "x
 x - 3", and change the following uses of x to use that new name, and the program would still do the same thing. We exploit this in SSA by creating two new variables, x1 and x2, each of which is assigned only once. We likewise give distinguishing subscripts to all the other variables, and we get this:
x - 3", and change the following uses of x to use that new name, and the program would still do the same thing. We exploit this in SSA by creating two new variables, x1 and x2, each of which is assigned only once. We likewise give distinguishing subscripts to all the other variables, and we get this:
We've figured out which definition each use is referring to, except for one thing: the uses of y in the bottom block could be referring to either y1 or y2, depending on which way the control flow came from. So how do we know which one to use?
The answer is that we add a special statement, called a Φ (Phi) function, to the beginning of the last block. This statement will generate a new definition of y, y3, by "choosing" either y1 or y2, depending on which arrow control arrived from:

Now, the uses of y in the last block can simply use y3, and they'll obtain the correct value either way. You might ask at this point, do we need to add a Φ function for x too? The answer is no; only one version of x, namely x2 is reaching this place, so there's no problem.
A more general question along the same lines is, given an arbitrary control flow graph, how can I tell where to insert Φ functions, and for what variables? This is a difficult question, but one that has an efficient solution that can be computed using a concept called dominance frontiers.
Note: the Φ functions are not actually implemented; instead, they're just markers for the compiler to place the value of all the variables, which are grouped together by the Φ function, in the same location in memory (or same register).
According to Kenny Zadeck Φ functions were originally known as phoney functions while SSA was being developed at IBM Research in the 1980s. The formal name of Φ function was only adopted when the work was first published in an academic paper.
Computing minimal SSA using dominance frontiers
First, we need the concept of a dominator: we say that a node A strictly dominates a different node B in the control flow graph if it's impossible to reach B without passing through A first. This is useful, because if we ever reach B we know that any code in A has run. We say that A dominates B (B is dominated by A) if either A strictly dominates B or A = B.Now we can define the dominance frontier: a node B is in the dominance frontier of a node A if A does not strictly dominate B, but does dominate some immediate predecessor of B (possibly node A is the immediate predecessor of B. Then, because any node dominates itself and node A dominates itself, node B is in the dominance frontier of node A.). From A's point of view, these are the nodes at which other control paths, which don't go through A, make their earliest appearance.
Dominance frontiers capture the precise places at which we need Φ functions: if the node A defines a certain variable, then that definition and that definition alone (or redefinitions) will reach every node A dominates. Only when we leave these nodes and enter the dominance frontier must we account for other flows bringing in other definitions of the same variable. Moreover, no other Φ functions are needed in the control flow graph to deal with A's definitions, and we can do with no less.
One algorithm for computing the dominance frontier set is:
for each node b
if the number of immediate predecessors of b ≥ 2
for each p in immediate predecessors of b
runner := p
while runner ≠ doms(b)
add b to runner’s dominance frontier set
runner := doms(runner)
Note: in the code above, an immediate predecessor of node n is any node from which control is transferred to node n, and doms(b) is the node that immediately dominates node b (a singleton set).
There is an efficient algorithm for finding dominance frontiers of each node. This algorithm was originally described in Cytron et al. 1991. Also useful is chapter 19 of the book "Modern compiler implementation in Java" by Andrew Appel (Cambridge University Press, 2002). See the paper for more details.
Keith D. Cooper, Timothy J. Harvey, and Ken Kennedy of Rice University
Rice University
William Marsh Rice University, commonly referred to as Rice University or Rice, is a private research university located on a heavily wooded campus in Houston, Texas, United States...
describe an algorithm in their paper titled A Simple, Fast Dominance Algorithm. The algorithm uses well-engineered data structures to improve performance.
Variations that reduce the number of Φ functions
"Minimal" SSA inserts the minimal number of Φ functions required to ensure that each name is assigned a value exactly once and that each reference (use) of a name in the original program can still refer to a unique name. (The latter requirement is needed to ensure that the compiler can write down a name for each operand in each operation.)However, some of these Φ functions could be dead
Dead code elimination
In compiler theory, dead code elimination is a compiler optimization to remove code which does not affect the program results. Removing such code has two benefits: it shrinks program size, an important...
. For this reason, minimal SSA does not necessarily produce the fewest number of Φ functions that are needed by a specific procedure. For some types of analysis, these Φ functions are superfluous and can cause the analysis to run less efficiently.
Pruned SSA
Pruned SSA form is based on a simple observation: Φ functions are only needed for variables that are "live" after the Φ function. (Here, "live" means that the value is used along some path that begins at the Φ function in question.) If a variable is not live, the result of the Φ function cannot be used and the assignment by the Φ function is dead.Construction of pruned SSA form uses live variable information
Live variable analysis
In compiler theory, live variable analysis is a classic data flow analysis performed by compilers to calculate for each program point the variables that may be potentially read before their next write, that is, the variables that are live at the exit from each program point.Stated simply: a...
in the Φ function insertion phase to decide whether a given Φ function is needed. If the original variable name isn't live at the Φ function insertion point, the Φ function isn't inserted.
Another possibility is to treat pruning as a dead code elimination
Dead code elimination
In compiler theory, dead code elimination is a compiler optimization to remove code which does not affect the program results. Removing such code has two benefits: it shrinks program size, an important...
problem. Then, a Φ function is live only if any use in the input program will be rewritten to it, or if it will be used as an argument in another Φ function. When entering SSA form, each use is rewritten to the nearest definition that dominates it. A Φ function will then be considered live as long as it is the nearest definition that dominates at least one use, or at least one argument of a live Φ.
Semi-pruned SSA
Semi-pruned SSA form is an attempt to reduce the number of Φ functions without incurring the relatively high cost of computing live variable information. It is based on the following observation: if a variable is never live upon entry into a basic block, it never needs a Φ function. During SSA construction, Φ functions for any "block-local" variables are omitted.Computing the set of block-local variables is a simpler and faster procedure than full live variable analysis, making semi-pruned SSA form more efficient to compute than pruned SSA form. On the other hand, semi-pruned SSA form will contain more Φ functions.
Converting out of SSA form
As SSA form is no longer useful for direct execution, it is frequently used "on top of" another IR with which it remains in direct correspondence. This can be accomplished by "constructing" SSA as a set of functions which map between parts of the existing IR (basic blocks, instructions, operands, etc.) and its SSA counterpart. When the SSA form is no longer needed, these mapping functions may be discarded, leaving only the now-optimized IR.Performing optimizations on SSA form usually leads to entangled SSA-Webs, meaning there are phi instructions whose operands do not all have the same root operand. In such cases color-out algorithms are used to come out of SSA. Naive algorithms introduce a copy along each predecessor path which caused a source of different root symbol to be put in phi than the destination of phi. There are multiple algorithms for coming out of SSA with fewer copies, most use interference graphs or some approximation of it to do copy coalescing.
Extensions
Extensions to SSA form can be divided into two categories.Renaming scheme extensions alter the renaming criterion. Recall that SSA form renames each variable when it is assigned a value. Alternative schemes include static single use form (which renames each variable at each statement when it is used) and static single information form (which renames each variable when it is assigned a value, and at the post-dominance frontier).
Feature-specific extensions retain the single assignment property for variables, but incorporate new semantics to model additional features. Some feature-specific extensions model high-level programming language features like arrays, objects and aliased pointers. Other feature-specific extensions model low-level architectural features like speculation and predication.
Compilers using SSA form
SSA form is a relatively recent development in the compiler community. As such, many older compilers only use SSA form for some part of the compilation or optimization process, but most do not rely on it. Examples of compilers that rely heavily on SSA form include:- The ETH Oberon-2Oberon-2Oberon-2 is an extension of the original Oberon programming language that adds limited reflection and object-oriented programming facilities, open arrays as pointer base types, read-only field export and reintroduces the FOR loop from Modula-2....
compiler was one of the first public projects to incorporate "GSA", a variant of SSA.
- The LLVM Compiler Infrastructure uses SSA form for all scalar register values (everything except memory) in its primary code representation. SSA form is only eliminated once register allocation occurs, late in the compile process (often at link time).
- The Open64Open64Open64 is an open source, optimizing compiler for the Itanium and x86-64 microprocessor architectures. It derives from the SGI compilers for the MIPS R10000 processor, called MIPSPro. It was initially released in 2000 as GNU GPL software under the name Pro64. The following year, University of...
compiler uses SSA form in its global scalar optimizer, though the code is brought into SSA form before and taken out of SSA form afterwards. Open64 uses extensions to SSA form to represent memory in SSA form as well as scalar values.
- As of version 4 (released in April 2005) GCC, the GNU Compiler CollectionGNU Compiler CollectionThe GNU Compiler Collection is a compiler system produced by the GNU Project supporting various programming languages. GCC is a key component of the GNU toolchain...
, makes extensive use of SSA. The frontends generate "GENERIC" code which is then converted into "GIMPLE" code by the "gimplifier". High-level optimizations are then applied on the SSA form of "GIMPLE". The resulting optimized intermediate code is then translated into RTLRegister Transfer LanguageIn computer science, register transfer language is a term used to describe a kind of intermediate representation that is very close to assembly language, such as that which is used in a compiler. Academic papers and textbooks also often use a form of RTL as an architecture-neutral assembly language...
, on which low-level optimizations are applied. The architecture-specific backends finally turn RTL into assembly languageAssembly languageAn assembly language is a low-level programming language for computers, microprocessors, microcontrollers, and other programmable devices. It implements a symbolic representation of the machine codes and other constants needed to program a given CPU architecture...
.
- IBMIBMInternational Business Machines Corporation or IBM is an American multinational technology and consulting corporation headquartered in Armonk, New York, United States. IBM manufactures and sells computer hardware and software, and it offers infrastructure, hosting and consulting services in areas...
's open source adaptive Java virtual machineJava Virtual MachineA Java virtual machine is a virtual machine capable of executing Java bytecode. It is the code execution component of the Java software platform. Sun Microsystems stated that there are over 4.5 billion JVM-enabled devices.-Overview:...
, Jikes RVM, uses extended Array SSA, an extension of SSA that allows analysis of scalars, arrays, and object fields in a unified framework. Extended Array SSA analysis is only enabled at the maximum optimization level, which is applied to the most frequently executed portions of code.
- In 2002, researchers modified IBM's JikesRVM (named Jalapeño at the time) to run both standard Java byte-code and a typesafe SSA (SafeTSASafeTSASafeTSA is a static single assignment form intermediate representation capable of representing all of the type safety of the Java programming language and the standard Java Virtual Machine byte-code....
) byte-code class files, and demonstrated significant performance benefits to using the SSA byte-code.
- Sun MicrosystemsSun MicrosystemsSun Microsystems, Inc. was a company that sold :computers, computer components, :computer software, and :information technology services. Sun was founded on February 24, 1982...
' Java HotSpot Virtual Machine uses an SSA-based intermediate language in its JIT compiler. - MonoMono (software)Mono, pronounced , is a free and open source project led by Xamarin to create an Ecma standard compliant .NET-compatible set of tools including, among others, a C# compiler and a Common Language Runtime....
uses SSA in its JIT compiler called Mini. - jackcc is an open-source compiler for the academic instruction set Jackal 3.0. It uses a simple 3-operand code with SSA for its intermediate representation. As an interesting variant, it replaces Φ functions with a so-called SAME instruction, which instructs the register allocator to place the two live ranges into the same physical register.
- Although not a compiler, the Boomerang decompilerDecompilerA decompiler is the name given to a computer program that performs, as far as possible, the reverse operation to that of a compiler. That is, it translates a file containing information at a relatively low level of abstraction into a form having a higher level of abstraction...
uses SSA form in its internal representation. SSA is used to simplify expression propagation, identifying parameters and returns, preservation analysis, and more. - Portable.NETPortable.NETPart of the DotGNU project, Portable.NET is a free software and open source software initiative aiming to build a portable toolchain and runtime for Common Language Infrastructure applications. The project focuses on compatibility with the ECMA-334 and ECMA-335 standards and support for .NET's...
uses SSA in its JIT compiler. - libFirm a completely graph based SSA intermediate representation for compilers. libFirm uses SSA form for all scalar register values until code generation by use of an SSA-aware register allocator.
- The Illinois Concert Compiler circa 1994 http://www-csag.ucsd.edu/projects/concert.html used a variant of SSA called SSU (Static Single Use) which renames each variable when it is assigned a value, and in each conditional context in which that variable is used; essentially the static single information form mentioned above. The SSU form is documented in John Plevyak's Ph.D Thesis.
- The COINS compiler uses SSA form optimizations as explained here: http://www.is.titech.ac.jp/~sassa/coins-www-ssa/english/
- The ChromiumChromium (web browser)Chromium is the open source web browser project from which Google Chrome draws its source code. The project's hourly Chromium snapshots appear essentially similar to the latest builds of Google Chrome aside from the omission of certain Google additions, most noticeable among them: Google's...
V8 JavaScript engine implements SSA in its Crankshaft compiler infrastructure as announced in December 2010
- PyPyPyPyPyPy is a Python interpreter and JIT compiler. PyPy focuses on speed, efficiency and 100% compatibility with the original CPython interpreter.- Details and motivation :...
uses a linear SSA representation for traces in its JIT compiler.
- Android's Dalvik virtual machine uses SSA in its JIT compiler.
- The Standard ML compiler MLtonMLtonMLton is an open source, whole-program optimizing compiler for the Standard ML programming language.MLton aims to produce fast executables, and to encourage rapid prototyping and modular programming by eliminating performance penalties often associated with the use of high-level language...
uses SSA in one of its intermediate languages.
General references
Also available in JavaJava (programming language)
Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
(ISBN 0-521-82060-X 2002) and C
C (programming language)
C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
(ISBN 0-521-60765-5, 199 8) versions.
External links
- Bosscher, Steven; and Novillo, Diego. GCC gets a new Optimizer Framework. An article about GCC's use of SSA and how it improves over older IRs.
- The SSA Bibliography. Extensive catalogue of SSA research papers.
- Zadeck, F. Kenneth. "The Development of Static Single Assignment Form", December 2007 talk on the origins of SSA.

