Star coloring
Encyclopedia
In graph-theoretic
mathematics
, a star coloring of a graph G is a (proper) vertex coloring
in which every path on four vertices
uses at least three distinct colors. Equivalently, in a star coloring, the induced subgraphs formed by the vertices of any two colors has connected component
s that are star graphs. Star coloring has been introduced by .
The star chromatic number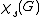
of G is the least number of colors needed to star color G.
One generalization of star coloring is the closely related concept of acyclic coloring
, where it is required that every cycle uses at least three colors, so the two-color induced subgraphs are forests. If we denote the acyclic chromatic number of a graph G by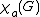
, we have that 
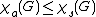, and in fact every star coloring of G is an acyclic coloring.
The star chromatic number has been proved to be bounded on every proper minor closed class by . This results was further generalized by to all low-tree-depth colorings (standard coloring and star coloring being low-tree-depth colorings with respective parameter 1 and 2).
to determine whether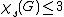
, even when G is a graph that is both planar
and bipartite
.
showed that finding an optimal star coloring is NP-hard
even when G is a bipartite graph.
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a star coloring of a graph G is a (proper) vertex coloring
Graph coloring
In graph theory, graph coloring is a special case of graph labeling; it is an assignment of labels traditionally called "colors" to elements of a graph subject to certain constraints. In its simplest form, it is a way of coloring the vertices of a graph such that no two adjacent vertices share the...
in which every path on four vertices
Path
Path, pathway or PATH may refer to:-Path:* Course , the intended path of a vehicle over the surface of the Earth* Trail, hiking trail, footpath, or bridle path...
uses at least three distinct colors. Equivalently, in a star coloring, the induced subgraphs formed by the vertices of any two colors has connected component
Connected component
Connected components are part of topology and graph theory, two related branches of mathematics.* For the graph-theoretic concept, see connected component .* In topology: connected component .Implementations:...
s that are star graphs. Star coloring has been introduced by .
The star chromatic number
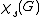of G is the least number of colors needed to star color G.One generalization of star coloring is the closely related concept of acyclic coloring
Acyclic coloring
In graph theory, an acyclic coloring is a vertex coloring in which every 2-chromatic subgraph is acyclic.The acyclic chromatic number A of a graph G is the least number of colors needed in any acyclic coloring of G....
, where it is required that every cycle uses at least three colors, so the two-color induced subgraphs are forests. If we denote the acyclic chromatic number of a graph G by
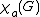, we have that 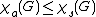, and in fact every star coloring of G is an acyclic coloring.The star chromatic number has been proved to be bounded on every proper minor closed class by . This results was further generalized by to all low-tree-depth colorings (standard coloring and star coloring being low-tree-depth colorings with respective parameter 1 and 2).
Complexity
It was demonstrated by that it is NP-completeNP-complete
In computational complexity theory, the complexity class NP-complete is a class of decision problems. A decision problem L is NP-complete if it is in the set of NP problems so that any given solution to the decision problem can be verified in polynomial time, and also in the set of NP-hard...
to determine whether
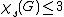, even when G is a graph that is both planarPlanar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints...
and bipartite
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
.
showed that finding an optimal star coloring is NP-hard
NP-hard
NP-hard , in computational complexity theory, is a class of problems that are, informally, "at least as hard as the hardest problems in NP". A problem H is NP-hard if and only if there is an NP-complete problem L that is polynomial time Turing-reducible to H...
even when G is a bipartite graph.
External links
- Star colorings and acyclic colorings (1973), present at the Research Experiences for Graduate Students (REGS) at the University of Illinois, 2008.