
Square of opposition
Encyclopedia
In the system of Aristotelian logic
, the square of opposition is a diagram representing the different ways in which each of the four proposition
s of the system are logically related ('opposed') to each of the others. The system is also useful in the analysis of syllogistic logic
, serving to identify the allowed logical conversions from one type to another.
Every categorical proposition can be reduced to one of four logical form
s. These are:
In tabular form:
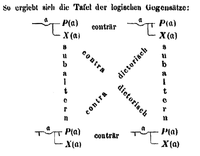
Aristotle states (in chapters six and seven of the Peri hermaneias (Περὶ Ἑρμηνείας, Latin De Interpretatione, English 'On Exposition'), that there are certain logical relationships between these four kinds of proposition. He says that to every affirmation there corresponds exactly one negation, and that every affirmation and its negation are 'opposed' such that always one of them must be true, and the other false. A pair of affirmative and negative statements he calls a 'contradiction' (in medieval Latin, contradictio). Examples of contradictories are 'every man is white' and 'not every man is white', 'no man is white' and 'some man is white'.
'Contrary' (medieval: contrariae) statements, are such that both cannot at the same time be true. Examples of these are the universal affirmative 'every man is white', and the universal negative 'no man is white'. These cannot be true at the same time. However, these are not contradictories because both of them may be false. For example, it is false that every man is white, since some men are not white. Yet it is also false that no man is white, since there are some white men.
Since every statement has a contradictory opposite, and since a contradictory is true when its opposite is false, it follows that the opposites of contraries (which the medievals called subcontraries, subcontrariae) can both be true, but they cannot both be false. Since subcontraries are negations of universal statements, they were called 'particular' statements by the medieval logicians.
A further logical relationship implied by this, though not mentioned explicitly by Aristotle, is subalternation (subalternatio). This is a relation between a particular statement and a universal statement such that the particular is implied by the other. For example, if 'every man is white' is true, its contrary 'no man is white' is false. Therefore the contradictory 'some man is white' is true. Similarly the universal 'no man is white' implies the particular 'not every man is white'.
In summary:
These relationships became the basis of a diagram originating with Boethius and used by medieval logicians to classify the logical relationships. The propositions are placed in the four corners of a square, and the relations represented as lines drawn between them, whence the name 'The Square of Opposition'.
. 'Some A is B' seems to imply 'something is A'. For example 'Some man is white' seems to imply that at least one thing is a man, namely the man who has to be white if 'some man is white' is true. But 'some man is not white' also seems to imply that something is a man, namely the man who is not white if 'some man is not white' is true. But Aristotelian logic requires that necessarily one of these statements is true. Both cannot be false. Therefore (since both imply that something is a man) it follows that necessarily something is a man, i.e. men exist. But (as Abelard points out, in the Dialectica) surely men might not exist?
Abelard also points out that subcontraries containing subject terms denoting nothing, such as 'a man who is a stone', are both false.
[in progress: Mill on the problem of existential import, Strawson's answer, Parsons's answer]
 In the 19th century, George Boole
In the 19th century, George Boole
argued for requiring existential import on both terms in particular claims (I and O), but allowing all terms of universal claims (A and E) to lack existential import. This decision made Venn diagram
s particularly easy to use for term logic. The square of opposition, under this Boolean set of assumptions, is often called the modern Square of opposition. In the modern square of opposition, A and O claims are contradictories, as are E and I, but all other forms of opposition cease to hold; there are no contraries, subcontraries, or subalterns. Thus, from a modern point of view, it often makes sense to talk about "the" opposition of a claim, rather than insisting as older logicians did that a claim has several different opposites, which are in different kinds of opposition with the claim.
Frege's Begriffsschrift
also presents a square of oppositions, organised in an almost identical manner to the classical square, showing the contradictories, subalternates and contraries between four formulae constructed from universal quantification, negation and implication.
. It has been proven that both the square and the hexagon, followed by a “logical cube”, belong to a regular series of n-dimensional objects called “logical bi-simplexes of dimension n.” The pattern also goes even beyond this.
Term logic
In philosophy, term logic, also known as traditional logic or aristotelian logic, is a loose name for the way of doing logic that began with Aristotle and that was dominant until the advent of modern predicate logic in the late nineteenth century...
, the square of opposition is a diagram representing the different ways in which each of the four proposition
Proposition
In logic and philosophy, the term proposition refers to either the "content" or "meaning" of a meaningful declarative sentence or the pattern of symbols, marks, or sounds that make up a meaningful declarative sentence...
s of the system are logically related ('opposed') to each of the others. The system is also useful in the analysis of syllogistic logic
Syllogism
A syllogism is a kind of logical argument in which one proposition is inferred from two or more others of a certain form...
, serving to identify the allowed logical conversions from one type to another.
Summary
In traditional logic, a proposition (Latin: propositio) is a spoken assertion (oratio enunciativa), not the meaning of an assertion, as in modern philosophy of language and logic. A categorical proposition is a simple proposition containing two terms, subject and predicate, in which the predicate is either asserted or denied of the subject.Every categorical proposition can be reduced to one of four logical form
Logical form
In logic, the logical form of a sentence or set of sentences is the form obtained by abstracting from the subject matter of its content terms or by regarding the content terms as mere placeholders or blanks on a form...
s. These are:
- The so-called 'A' proposition, the universal affirmative (universalis affirmativa), whose form in Latin is 'omne S est P', usually translated as 'every S is a P'.
- The 'E' proposition, the universal negative (universalis negativa), Latin form 'nullum S est P', usually translated as 'no S are P'.
- The 'I' proposition, the particular affirmative (particularis affirmativa), Latin 'quoddam S est P', usually translated as 'some S are P'.
- The 'O' proposition, the particular negative (particularis negativa), Latin 'quoddam S non est P', usually translated as 'some S are not P'.
In tabular form:
| Name | Symbol | Latin | English | |
|---|---|---|---|---|
| Universal affirmative | A | Omne S est P | Every S is P | All S is P |
| Universal negative | E | Nullum S est P | No S is P | All S is not P |
| Particular affirmative | I | Quoddam S est P | Some S is P | Some S is P |
| Particular negative | O | Quoddam S non est P | Some S is not P | Some S is not P |
Aristotle states (in chapters six and seven of the Peri hermaneias (Περὶ Ἑρμηνείας, Latin De Interpretatione, English 'On Exposition'), that there are certain logical relationships between these four kinds of proposition. He says that to every affirmation there corresponds exactly one negation, and that every affirmation and its negation are 'opposed' such that always one of them must be true, and the other false. A pair of affirmative and negative statements he calls a 'contradiction' (in medieval Latin, contradictio). Examples of contradictories are 'every man is white' and 'not every man is white', 'no man is white' and 'some man is white'.
'Contrary' (medieval: contrariae) statements, are such that both cannot at the same time be true. Examples of these are the universal affirmative 'every man is white', and the universal negative 'no man is white'. These cannot be true at the same time. However, these are not contradictories because both of them may be false. For example, it is false that every man is white, since some men are not white. Yet it is also false that no man is white, since there are some white men.
Since every statement has a contradictory opposite, and since a contradictory is true when its opposite is false, it follows that the opposites of contraries (which the medievals called subcontraries, subcontrariae) can both be true, but they cannot both be false. Since subcontraries are negations of universal statements, they were called 'particular' statements by the medieval logicians.
A further logical relationship implied by this, though not mentioned explicitly by Aristotle, is subalternation (subalternatio). This is a relation between a particular statement and a universal statement such that the particular is implied by the other. For example, if 'every man is white' is true, its contrary 'no man is white' is false. Therefore the contradictory 'some man is white' is true. Similarly the universal 'no man is white' implies the particular 'not every man is white'.
In summary:
- Universal statements are contraries: 'every man is just' and 'no man is just' cannot be true together, although one may be true and the other false, and also both may be false (if at least one man is just, and at least one man is not just).
- Particular statements are subcontraries. 'Some man is just' and 'some man is not just' cannot be false together
- The universal affirmative and the particular affirmative are subalternates, because in Aristotelian semantics 'every A is B' implies 'some A is B'. Note that modern formal interpretations of English sentences interpret 'every A is B' as 'for any x, x is A implies x is B', which does not imply 'some x is A'. This is a matter of semantic interpretation, however, and does not mean, as is sometimes claimed, that Aristotelian logic is 'wrong'.
- The universal affirmative and the particular negative are contradictories. If some A is not B, not every A is B. Conversely, though this is not the case in modern semantics, it was thought that if every A is not B, some A is not B. This interpretation has caused difficulties (see below). While Aristotle's Greek does not represent the particular negative as 'some A is not B', but as 'not every A is B', Boethius in his commentary on the Peri hermaneias, renders the particular negative as 'quoddam A non est B', literally 'a certain A is not a B', and in all medieval writing on logic it is customary to represent the particular proposition in this way.
These relationships became the basis of a diagram originating with Boethius and used by medieval logicians to classify the logical relationships. The propositions are placed in the four corners of a square, and the relations represented as lines drawn between them, whence the name 'The Square of Opposition'.
The problem of existential import
Subcontraries, which medieval logicians represented in the form 'quoddam A est B' (some particular A is B) and 'quoddam A non est B' (some particular A is not B) cannot both be false, since their universal contradictory statements (every A is B / no A is B) cannot both be true. This leads to a difficulty that was first identified by Peter AbelardPeter Abelard
Peter Abelard was a medieval French scholastic philosopher, theologian and preeminent logician. The story of his affair with and love for Héloïse has become legendary...
. 'Some A is B' seems to imply 'something is A'. For example 'Some man is white' seems to imply that at least one thing is a man, namely the man who has to be white if 'some man is white' is true. But 'some man is not white' also seems to imply that something is a man, namely the man who is not white if 'some man is not white' is true. But Aristotelian logic requires that necessarily one of these statements is true. Both cannot be false. Therefore (since both imply that something is a man) it follows that necessarily something is a man, i.e. men exist. But (as Abelard points out, in the Dialectica) surely men might not exist?
- For with absolutely no man existing, neither the proposition 'every man is a man' is true nor 'some man is not a man'.
Abelard also points out that subcontraries containing subject terms denoting nothing, such as 'a man who is a stone', are both false.
- If 'every stone-man is a stone' is true, also its conversion per accidens is true ('some stone-men are stones'). But no stone is a stone-man, because neither this man nor that man etc. is a stone. But also this 'a certain stone-man is not a stone' is false by necessity, since it is impossible to suppose it is true.
[in progress: Mill on the problem of existential import, Strawson's answer, Parsons's answer]
Modern squares of opposition

George Boole
George Boole was an English mathematician and philosopher.As the inventor of Boolean logic—the basis of modern digital computer logic—Boole is regarded in hindsight as a founder of the field of computer science. Boole said,...
argued for requiring existential import on both terms in particular claims (I and O), but allowing all terms of universal claims (A and E) to lack existential import. This decision made Venn diagram
Venn diagram
Venn diagrams or set diagrams are diagrams that show all possible logical relations between a finite collection of sets . Venn diagrams were conceived around 1880 by John Venn...
s particularly easy to use for term logic. The square of opposition, under this Boolean set of assumptions, is often called the modern Square of opposition. In the modern square of opposition, A and O claims are contradictories, as are E and I, but all other forms of opposition cease to hold; there are no contraries, subcontraries, or subalterns. Thus, from a modern point of view, it often makes sense to talk about "the" opposition of a claim, rather than insisting as older logicians did that a claim has several different opposites, which are in different kinds of opposition with the claim.
Frege's Begriffsschrift
Begriffsschrift
Begriffsschrift is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book...
also presents a square of oppositions, organised in an almost identical manner to the classical square, showing the contradictories, subalternates and contraries between four formulae constructed from universal quantification, negation and implication.
Logical hexagons and other bi-simplexes
The square of opposition has been extended to a logical hexagon which includes the relationships of six statements. It was discovered independently by both Augustin Sesmat and Robert BlanchéRobert Blanché
Robert Blanché was an associate professor of philosophy at the University of Toulouse. He wrote many books addressing the philosophy of mathematics.-Works :...
. It has been proven that both the square and the hexagon, followed by a “logical cube”, belong to a regular series of n-dimensional objects called “logical bi-simplexes of dimension n.” The pattern also goes even beyond this.

