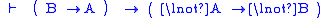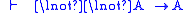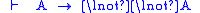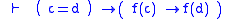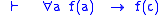Begriffsschrift - AbsoluteAstronomy.com

Begriffsschrift is a book on logic

Logic

In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...

by Gottlob Frege

Gottlob Frege

Friedrich Ludwig Gottlob Frege was a German mathematician, logician and philosopher. He is considered to be one of the founders of modern logic, and made major contributions to the foundations of mathematics. He is generally considered to be the father of analytic philosophy, for his writings on...

, published in 1879, and the formal system

Formal system

In formal logic, a formal system consists of a formal language and a set of inference rules, used to derive an expression from one or more other premises that are antecedently supposed or derived . The axioms and rules may be called a deductive apparatus...

set out in that book. It is generally considered the work that marks the birth of modern logic.

Begriffsschrift is usually translated as concept writing or concept notation; the full title of the book identifies it as "a formula

Formula

In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....

language

Language

Language may refer either to the specifically human capacity for acquiring and using complex systems of communication, or to a specific instance of such a system of complex communication...

, modelled on that of arithmetic

Arithmetic

Arithmetic or arithmetics is the oldest and most elementary branch of mathematics, used by almost everyone, for tasks ranging from simple day-to-day counting to advanced science and business calculations. It involves the study of quantity, especially as the result of combining numbers...

, of pure thought

Thought

"Thought" generally refers to any mental or intellectual activity involving an individual's subjective consciousness. It can refer either to the act of thinking or the resulting ideas or arrangements of ideas. Similar concepts include cognition, sentience, consciousness, and imagination...

." The Begriffsschrift was arguably the most important publication in logic

Logic

since Aristotle

Aristotle

Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...

founded the subject. Frege's motivation for developing his formal approach to logic resembled Leibniz's motivation for his calculus ratiocinator

Calculus ratiocinator

The Calculus Ratiocinator is a theoretical universal logical calculation framework, a concept described in the writings of Gottfried Leibniz, usually paired with his more frequently mentioned characteristica universalis, a universal conceptual language....

. Frege went on to employ his logical calculus in his research on the foundations of mathematics

Foundations of mathematics

Foundations of mathematics is a term sometimes used for certain fields of mathematics, such as mathematical logic, axiomatic set theory, proof theory, model theory, type theory and recursion theory...

, carried out over the next quarter century.

Notation and the system

The calculus contains the first appearance of quantified variables, and is essentially classical bivalent second-order logic

Second-order logic

In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....

with identity

Identity (mathematics)

In mathematics, the term identity has several different important meanings:*An identity is a relation which is tautologically true. This means that whatever the number or value may be, the answer stays the same. For example, algebraically, this occurs if an equation is satisfied for all values of...

, albeit presented using a highly idiosyncratic two-dimensional notation

Mathematical notation

Mathematical notation is a system of symbolic representations of mathematical objects and ideas. Mathematical notations are used in mathematics, the physical sciences, engineering, and economics...

: connectives and quantifiers are written using lines connecting formulas, rather than the symbols ¬, ∧, and ∀ in use today. For example, that judgement B materially implies judgement A, i.e.

is written as

.

In the first chapter, Frege defines basic ideas and notation, like proposition ("judgement"), the universal quantifier ("the generality"), the conditional, negation and the "sign for identity of content"

(which he used to indicate both material equivalence and identity

Identity

-Philosophical topics:* Identity , also called sameness, is whatever makes an entity definable and recognizable* Law of identity, principle of logic stating that an object is the same as itself...

proper); in the second chapter he declares nine formalized propositions as axioms.

Basic concept	Frege's notation	Modern notations
Judging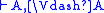
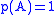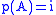Negation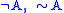
Conditional (implication)
Universal quantification
Existential quantification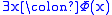
Content identity (equivalence/identity)		A ↔ B

In chapter 1, §5, Frege defines the conditional as follows:

"Let A and B refer to judgeable contents, then the four possibilities are:

A is asserted, B is asserted;
A is asserted, B is negated;
A is negated, B is asserted;
A is negated, B is negated.

Let

signify that the third of those possibilities does not obtain, but one of the three others does. So if we negate ,
that means the third possibility is valid, i.e. we negate A and assert B."

The calculus in Frege's work

Frege declared nine of his propositions to be axiom

Axiom

In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...

s, and justified them by arguing informally that, given their intended meanings, they express intuitive truths. Re-expressed in contemporary notation, these axioms are:

These are propositions 1, 2, 8, 28, 31, 41, 52, 54, and 58 in the Begriffschrifft. (1)-(3) govern material implication, (4)-(6) negation

Negation

In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...

, (7) and (8) identity

Identity (mathematics)

, and (9) the universal quantifier. (7) expresses Leibniz's indiscernibility of identicals

Indiscernibles

In mathematical logic, indiscernibles are objects which cannot be distinguished by any property or relation defined by a formula. Usually only first-order formulas are considered...

, and (8) asserts that identity is a reflexive relation

Reflexive relation

In mathematics, a reflexive relation is a binary relation on a set for which every element is related to itself, i.e., a relation ~ on S where x~x holds true for every x in S. For example, ~ could be "is equal to".-Related terms:...

.

All other propositions are deduced from (1)-(9) by invoking any of the following inference rules:

Modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...

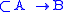allows us to infer from and ;
The rule of generalization
Generalization (logic)
In mathematical logic, generalization is an inference rule of predicate calculus. It states that if \vdash P has been derived, then \vdash \forall x \, P can be derived....

allows us to infer from if x does not occur in P;
The rule of substitution
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...

, which Frege does not state explicitly. This rule is much harder to articulate precisely than the two preceding rules, and Frege invokes it in ways that are not obviously legitimate.

The main results of the third chapter, titled "Parts from a general series theory," concern what is now called the ancestral

Ancestral relation

In mathematical logic, the ancestral relation of an arbitrary binary relation R is defined below.The ancestral makes its first appearance in Frege's Begriffsschrift. Frege later employed it in his Grundgesetze as part of his definition of the natural numbers...

of a relation R. "a is an R-ancestor of b" is written "aR*b".

Frege applied the results from the Begriffsschrifft, including those on the ancestral of a relation, in his later work The Foundations of Arithmetic
The Foundations of Arithmetic
Die Grundlagen der Arithmetik is a book by Gottlob Frege, published in 1884, in which he investigates the philosophical foundations of arithmetic. In a tour de force of literary and philosophical merit, Frege demolished other theories of number and developed his own theory of numbers...

. Thus, if we take xRy to be the relation y=x+1, then 0R*y is the predicate "y is a natural number." (133) says that if x, y, and z are natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

s, then one of the following must hold: x<y, x=y, or y<x. This is the so-called "law of trichotomy".

Influence on other works

For a careful recent study of how the Begriffsschrift was reviewed in the German mathematical literature, see Vilko (1998). Some reviewers, especially Ernst Schröder

Ernst Schröder

Ernst Schröder was a German mathematician mainly known for his work on algebraic logic. He is a major figure in the history of mathematical logic , by virtue of summarizing and extending the work of George Boole, Augustus De Morgan, Hugh MacColl, and especially Charles Peirce...

, were on the whole favorable. All work in formal logic subsequent to the Begriffsschrift is indebted to it, because its second-order logic was the first formal logic capable of representing a fair bit of mathematics and natural language.

Some vestige of Frege's notation survives in the "turnstile

Turnstile (symbol)

In mathematical logic and computer science the symbol \vdash has taken the name turnstile because of its resemblance to a typical turnstile if viewed from above. It is also referred to as tee and is often read as "yields", "proves", "satisfies" or "entails"...

" symbol

derived from his "Inhaltsstrich"´(i.e. content-dash) ── and "Urteilsstrich" (judging/infering-dash) │. Frege used these symbols in the Begriffsschrift in the unified form ├─ for declaring that a proposition is true. In his later "Grundgesetze" he revises slightly his interpretation of the ├─ symbol.

In "Begriffsschrift" the "Definitionsdoppelstrich" (i.e. definition-double-dash) │├─ indicates that a proposition is a definition. Furthermore, the negation sign

can be read as a combination of the horizontal Inhaltsstrich with a vertical negation stroke. This negation symbol was reintroduced by Arend Heyting

Arend Heyting

Arend Heyting was a Dutch mathematician and logician. He was a student of Luitzen Egbertus Jan Brouwer at the University of Amsterdam, and did much to put intuitionistic logic on a footing where it could become part of mathematical logic...

in 1930 to distinguish intuitionistic from classical negation. It also appears in Gerhard Gentzen's doctoral dissertation.

In the Tractatus Logico Philosophicus, Ludwig Wittgenstein

Ludwig Wittgenstein

Ludwig Josef Johann Wittgenstein was an Austrian philosopher who worked primarily in logic, the philosophy of mathematics, the philosophy of mind, and the philosophy of language. He was professor in philosophy at the University of Cambridge from 1939 until 1947...

pays homage to Frege by employing the term Begriffsschrift as a synonym for logical formalism.

Frege's 1892 essay, "Sense and reference

Sense and reference

Sinn and bedeutung are usually translated, respectively, as sense and reference. Two different aspects of some terms' meanings, a term's reference is the object that the term refers to, while the term's sense is the way that the term refers to that object.Sinn and bedeutung were introduced by...

" recants some of the conclusions of the Begriffsschrifft about identity (denoted in mathematics by the = sign). In particular, he rejects the "Begriffsschrift" view that the identity predicate expresses a relationship between names, in favor of the conclusion that it expresses a relationship between the objects that are denoted by those names.

A quotation

"If the task of philosophy is to break the domination of words over the human mind [...], then my concept notation, being developed for these purposes, can be a useful instrument for philosophers [...] I believe the cause of logic has been advanced already by the invention of this concept notation." (Preface to the Begriffsschrift)

Notation and the system

The calculus in Frege's work

Influence on other works

A quotation

Further reading