Spherical model
Encyclopedia
The spherical model in statistical mechanics
is a model of ferromagnetism
similar to the Ising model
, which was solved in 1952 by T.H. Berlin and M. Kac
. It has the remarkable property that when applied to systems of dimension d greater than four, the critical exponents which govern the behaviour of the system near the critical point are independent of d and the geometry of the system. It is one of the few models of ferromagnetism that can be solved exactly in the presence of an external field.
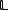which contains N sites. For each site j of 
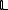, a spin 
which interacts only with its nearest neighbours and an external field H. It differs from the Ising model in that the 
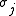are no longer restricted to 
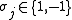, but can take all real values, subject to the constraint that
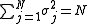
which in a homogenous system ensures that the average of the square of any spin is one, as in the usual Ising model.
The partition function
generalizes from that of the Ising model
to
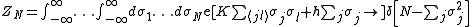
where
is the Dirac delta function
,
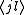are the edges of the lattice, and 
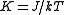and 
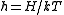, where T is the temperature of the system, k is Boltzmann's constant and J the coupling constant of the nearest-neighbour interactions.
Berlin and Kac saw this as an approximation to the usual Ising model, arguing that the
-summation in the Ising model can be viewed as a sum over all corners of an N-dimensional hypercube
in
-space. The becomes an integration
over the surface of a hypersphere passing through all such corners.
It was rigorously proved by Kac and C.J. Thompson that the spherical model is a limiting case of the N-vector model.
yields an equation describing the magnetization
M of the system
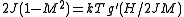
for the function g defined as
The internal energy
per site is given by
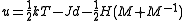
an exact relation relating internal energy and magnetization.
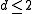the critical temperature occurs at absolute zero
, resulting in no phase transition for the spherical model. For d greater than 2, the spherical model exhibits the typical ferromagnetic behaviour, with a finite Curie temperature where ferromagnetism ceases. The critical behaviour of the spherical model was derived in the completely general circumstances that the dimension d may be a real non-integer dimension.
The critical exponents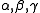
and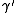 
in the zero-field case which dictate the behaviour of the system close to were derived to be
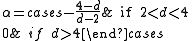
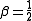
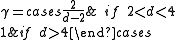
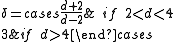
which are independent of the dimension of d when it is greater than four, the dimension being able to take any real value.
Statistical mechanics
Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...
is a model of ferromagnetism
Ferromagnetism
Ferromagnetism is the basic mechanism by which certain materials form permanent magnets, or are attracted to magnets. In physics, several different types of magnetism are distinguished...
similar to the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
, which was solved in 1952 by T.H. Berlin and M. Kac
Mark Kac
Mark Kac was a Polish mathematician. His main interest was probability theory. His question, "Can one hear the shape of a drum?" set off research into spectral theory, with the idea of understanding the extent to which the spectrum allows one to read back the geometry. Kac completed his Ph.D...
. It has the remarkable property that when applied to systems of dimension d greater than four, the critical exponents which govern the behaviour of the system near the critical point are independent of d and the geometry of the system. It is one of the few models of ferromagnetism that can be solved exactly in the presence of an external field.
Formulation
The model describes a set of particles on a lattice which contains N sites. For each site j of , a spin which interacts only with its nearest neighbours and an external field H. It differs from the Ising model in that the 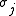are no longer restricted to 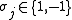, but can take all real values, subject to the constraint that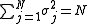which in a homogenous system ensures that the average of the square of any spin is one, as in the usual Ising model.
The partition function
Partition function (statistical mechanics)
Partition functions describe the statistical properties of a system in thermodynamic equilibrium. It is a function of temperature and other parameters, such as the volume enclosing a gas...
generalizes from that of the Ising model
Ising model
The Ising model is a mathematical model of ferromagnetism in statistical mechanics. The model consists of discrete variables called spins that can be in one of two states . The spins are arranged in a graph , and each spin interacts with its nearest neighbors...
to
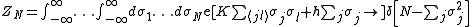
where
is the Dirac delta functionDirac delta function
The Dirac delta function, or δ function, is a generalized function depending on a real parameter such that it is zero for all values of the parameter except when the parameter is zero, and its integral over the parameter from −∞ to ∞ is equal to one. It was introduced by theoretical...
,
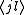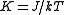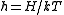are the edges of the lattice, and and , where T is the temperature of the system, k is Boltzmann's constant and J the coupling constant of the nearest-neighbour interactions.Berlin and Kac saw this as an approximation to the usual Ising model, arguing that the
-summation in the Ising model can be viewed as a sum over all corners of an N-dimensional hypercubeHypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
in
-space. The becomes an integrationIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
over the surface of a hypersphere passing through all such corners.
It was rigorously proved by Kac and C.J. Thompson that the spherical model is a limiting case of the N-vector model.
Equation of state
Solving the partition function and using a calculation of the free energyThermodynamic free energy
The thermodynamic free energy is the amount of work that a thermodynamic system can perform. The concept is useful in the thermodynamics of chemical or thermal processes in engineering and science. The free energy is the internal energy of a system less the amount of energy that cannot be used to...
yields an equation describing the magnetization
Magnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
M of the system
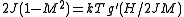
for the function g defined as
The internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
per site is given by
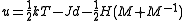
an exact relation relating internal energy and magnetization.
Critical behaviour
For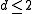 the critical temperature occurs at absolute zeroAbsolute zero
Absolute zero is the theoretical temperature at which entropy reaches its minimum value. The laws of thermodynamics state that absolute zero cannot be reached using only thermodynamic means....
, resulting in no phase transition for the spherical model. For d greater than 2, the spherical model exhibits the typical ferromagnetic behaviour, with a finite Curie temperature where ferromagnetism ceases. The critical behaviour of the spherical model was derived in the completely general circumstances that the dimension d may be a real non-integer dimension.
The critical exponents
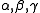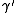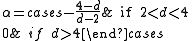
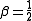
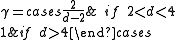
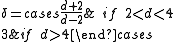
and in the zero-field case which dictate the behaviour of the system close to were derived to bewhich are independent of the dimension of d when it is greater than four, the dimension being able to take any real value.