
Sorgenfrey plane
Encyclopedia
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
, the Sorgenfrey plane is a frequently-cited counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
to many otherwise plausible-sounding conjectures. It consists of the product of two copies of the Sorgenfrey line, which is the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
 under the half-open interval topology. The Sorgenfrey line and plane are named for the American mathematician Robert Sorgenfrey
under the half-open interval topology. The Sorgenfrey line and plane are named for the American mathematician Robert SorgenfreyRobert Sorgenfrey
Robert Henry Sorgenfrey was an American mathematician and Professor Emeritus of Mathematics at the University of California, Los Angeles....
.
A basis for the Sorgenfrey plane, denoted
 from now on, is therefore the set of rectangle
from now on, is therefore the set of rectangleRectangle
In Euclidean plane geometry, a rectangle is any quadrilateral with four right angles. The term "oblong" is occasionally used to refer to a non-square rectangle...
s that include the west edge, southwest corner, and south edge, and omit the southeast corner, east edge, northeast corner, north edge, and northwest corner. Open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
s in
 are unions of such rectangles.
are unions of such rectangles. is an example of a space that is a product of Lindelöf space
is an example of a space that is a product of Lindelöf spaceLindelöf space
In mathematics, a Lindelöf space is a topological space in which every open cover has a countable subcover. The Lindelöf property is a weakening of the more commonly used notion of compactness, which requires the existence of a finite subcover....
s that is not itself a Lindelöf space. It is also an example of a space that is a product of normal space
Normal space
In topology and related branches of mathematics, a normal space is a topological space X that satisfies Axiom T4: every two disjoint closed sets of X have disjoint open neighborhoods. A normal Hausdorff space is also called a T4 space...
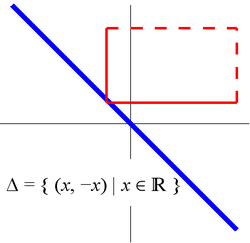
s that is not itself normal. The so-called anti-diagonal
 is a discrete
is a discreteDiscrete space
In topology, a discrete space is a particularly simple example of a topological space or similar structure, one in which the points are "isolated" from each other in a certain sense.- Definitions :Given a set X:...
subset of this space, and this is a non-separable subset of the separable space
 . It shows that separability does not inherit to closed subspaces. Note that
. It shows that separability does not inherit to closed subspaces. Note that  and
and  are closed sets that cannot be separated by open sets, showing that
are closed sets that cannot be separated by open sets, showing that  is not normal.
is not normal.

