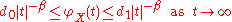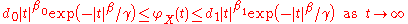Smoothness (probability theory)
Encyclopedia
In probability theory
and statistics
, smoothness of a density function is a measure which determines how many times the density function can be differentiated, or equivalently the limiting behavior of distribution’s characteristic function
.
Formally, we call the distribution of a random variable
X ordinary smooth of order β if its characteristic function
satisfies
for some positive constants d0, d1, β. The examples of such distributions are gamma, exponential
, uniform
, etc.
The distribution is called supersmooth of order β if its characteristic function satisfies
for some positive constants d0, d1, β, γ and constants β0, β1. Such supersmooth distributions have derivatives of all orders. Examples: normal, Cauchy
, mixture normal.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, smoothness of a density function is a measure which determines how many times the density function can be differentiated, or equivalently the limiting behavior of distribution’s characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
.
Formally, we call the distribution of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X ordinary smooth of order β if its characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
satisfies
for some positive constants d0, d1, β. The examples of such distributions are gamma, exponential
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
, uniform
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
, etc.
The distribution is called supersmooth of order β if its characteristic function satisfies
for some positive constants d0, d1, β, γ and constants β0, β1. Such supersmooth distributions have derivatives of all orders. Examples: normal, Cauchy
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
, mixture normal.