Smoluchowski equation
Encyclopedia
In physics, the diffusion equation with drift
term is often called Smoluchowski equation (after Marian von Smoluchowski).
, D a diffusion constant, ζ a friction coefficient,
and U(r, t) a potential. Then the Smoluchowski equation states that the density evolves according to
The diffusivity term
acts to smoothen out the density, while the drift term 
shifts the density towards regions of low potential 
. The equation is consistent with each particle moving according to a stochastic differential equation
, with a bias term
and a diffusivity 
. Physically, the drift term originates from a force 
being balanced by a viscous drag given by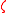 
.
The Smoluchowski equation is formally identical to the Fokker–Planck equation, the only difference being the physical meaning of w: a distribution of particles in space for the Smoluchowski equation, a distribution of particle velocities for the Fokker–Planck equation.
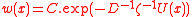
where
is a normalization constant. Thus, in steady-state, concentration highs are found in potential lows, and that the accumulation is more pronounced when diffusivity 
and/or the friction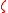 
is low. This distribution is formally identical to the Gibbs canonical distribution
in statistical physics, and very closely related to the Boltzmann distribution
.
Chandrasekhar
stated in 1943 that the diffusion equation with drift term
"is sometimes called Smoluchowski equation".
Since then, this has become the standard nomenclature.
Other equations due to Smoluchowski are now usually given more specific names:
Drift
- Film and literature :* Drift , a 2002 Doctor Who novel* Drift , a series of Japanese films written and directed by Futoshi Jinno* Drift, 2007 experimental short film by Max Hattler* Drift , a fictional character...
term is often called Smoluchowski equation (after Marian von Smoluchowski).
The equation
Let w(r, t) be a densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, D a diffusion constant, ζ a friction coefficient,
and U(r, t) a potential. Then the Smoluchowski equation states that the density evolves according to
The diffusivity term
acts to smoothen out the density, while the drift term shifts the density towards regions of low potential . The equation is consistent with each particle moving according to a stochastic differential equationStochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
, with a bias term
and a diffusivity . Physically, the drift term originates from a force being balanced by a viscous drag given by 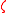.The Smoluchowski equation is formally identical to the Fokker–Planck equation, the only difference being the physical meaning of w: a distribution of particles in space for the Smoluchowski equation, a distribution of particle velocities for the Fokker–Planck equation.
Steady-state solution
A time-invariant solution to the Smoluchowski equation is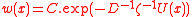where
is a normalization constant. Thus, in steady-state, concentration highs are found in potential lows, and that the accumulation is more pronounced when diffusivity and/or the friction 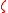is low. This distribution is formally identical to the Gibbs canonical distributionGibbs measure
In mathematics, the Gibbs measure, named after Josiah Willard Gibbs, is a probability measure frequently seen in many problems of probability theory and statistical mechanics. It is the measure associated with the Boltzmann distribution, and generalizes the notion of the canonical ensemble...
in statistical physics, and very closely related to the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
.
Other equations named for Smoluchowski
In the first half of the 20th century, a number of different equations were referred to as Smoluchowski's. In an influential review,Chandrasekhar
Chandrasekhar
Chandrasekhar or Chandra Shekhar is an Indian name and may refer to a number of individuals. Etymologically, the name comes from the Sanskrit words "चन्द्र ", meaning "moon", and "शेखर ", meaning "crest" or "crown" which is an epithet of Hindu god Shiva...
stated in 1943 that the diffusion equation with drift term
"is sometimes called Smoluchowski equation".
Since then, this has become the standard nomenclature.
Other equations due to Smoluchowski are now usually given more specific names:
- Einstein–Smoluchowski relationEinstein relation (kinetic theory)In physics the Einstein relation is a previously unexpected connection revealed independently by Albert Einstein in 1905 and by Marian Smoluchowski in their papers on Brownian motion...
- Smoluchowski coagulation equationSmoluchowski Coagulation EquationThe Smoluchowski coagulation equation is an integrodifferential equation introduced by Marian Smoluchowski in a seminal 1916 publication , describing the evolution of the number density of particles of size x at a time t...