
Small world routing
Encyclopedia
In network theory
, small world routing refers to routing methods for small-world network
s. Networks of this type are peculiar in that relatively short paths exist between any two nodes. Determining these paths, however, can be a difficult problem from the perspective of an individual routing node in the network if no further information is known about the network as a whole.
routing. This sort of routing depends on a relative reference point by which any node in the path can choose the next node it believes is closest to the destination. That is, there must be something to be greedy about. For example, this could be geographic location, IP address, etc. In the case of Milgram's original small-world experiment, participants knew the location and occupation of the final recipient and could therefore forward messages based on those parameters.
s where information about the destination's location in the underlying network is not available. Friend to friend networks are a particular example of this problem. In such networks, trust is ensured by the fact that you only know underlying information about nodes with whom you are already a neighbor.
One solution in this case, is to impose some sort of artificial addressing on the nodes in such a way that this addressing can be effectively used by greedy routing methods. A 2005 paper by a developer of the Freenet Project
discusses how this can be accomplished in friend to friend networks. Given the assumption that these networks exhibit small world properties, often as the result of real-world or acquaintance relationships, it should be possible to recover an embedded Kleinberg
small-world graph. This is accomplished by selecting random pairs of nodes and potentially swapping them based on an objective function that minimizes the product of all the distances between any given node and its neighbors.
An important problem involved with this solution is the possibility of local minima. This can occur if nodes are in a situation that is optimal only considering a local neighborhood, while ignoring the possibility of a higher optimality resulting from swaps with distant nodes. In the above paper, the authors proposed a simulated annealing
method where less-than-optimal swaps were made with a small probability. This probability was proportional to the value of making the switches. Another possible metaheuristic
optimization method is a tabu search
, which adds a memory to the swap decision. In its most simplistic form, a limited history of past swaps is remembered so that they will be excluded from the list of possible swapping nodes.
This method for constructing a reference base can also be adapted to distributed settings, where decisions can only be made at the level of individual nodes who have no knowledge of the overall network. It turns out that the only modification necessary is in the method for selecting pairs of random nodes. In a distributed setting, this is done by having each node periodically send out a random walker
terminating at a node to be considered for swapping.
 to another random vertex w is proportional to
to another random vertex w is proportional to 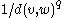 , where
, where 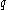 is the clustering coefficient
is the clustering coefficient
.
, without using the long range edges, can navigate from random vertices v->w on the grid in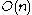 time. By following the guaranteed connections to our neighbors, we can move one unit at a time in the direction of our destination. This is also the case when the clustering component q large and the “long range” edges end up staying very close; we simply do not take advantage of the weaker ties in this model. When
time. By following the guaranteed connections to our neighbors, we can move one unit at a time in the direction of our destination. This is also the case when the clustering component q large and the “long range” edges end up staying very close; we simply do not take advantage of the weaker ties in this model. When 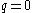 , the long range edges are uniformly connected at random which means the long range edges are “too random” to be used efficiently for decentralized search. Kleinberg has shown that the optimal clustering coefficient for this model is
, the long range edges are uniformly connected at random which means the long range edges are “too random” to be used efficiently for decentralized search. Kleinberg has shown that the optimal clustering coefficient for this model is 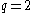 , or an inverse square distribution.
, or an inverse square distribution.
To reason why this is the case, if a circle of radius r is drawn around the initial node it will have nodal density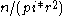 where n is the number of nodes in the circular area. As this circle gets expanded further out, the number of nodes in the given area increases proportional to
where n is the number of nodes in the circular area. As this circle gets expanded further out, the number of nodes in the given area increases proportional to 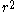 as the probability of having a random link with any node remains proportional
as the probability of having a random link with any node remains proportional  , meaning the probability of the original node having a weak tie with any node a given distance away is effectively independent of distance. Therefore, it is concluded that with
, meaning the probability of the original node having a weak tie with any node a given distance away is effectively independent of distance. Therefore, it is concluded that with 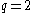 , long-range edges are evenly distributed over all distances, which is effective for letting us funnel to our final destination.
, long-range edges are evenly distributed over all distances, which is effective for letting us funnel to our final destination.
Network theory
Network theory is an area of computer science and network science and part of graph theory. It has application in many disciplines including statistical physics, particle physics, computer science, biology, economics, operations research, and sociology...
, small world routing refers to routing methods for small-world network
Small-world network
In mathematics, physics and sociology, a small-world network is a type of mathematical graph in which most nodes are not neighbors of one another, but most nodes can be reached from every other by a small number of hops or steps...
s. Networks of this type are peculiar in that relatively short paths exist between any two nodes. Determining these paths, however, can be a difficult problem from the perspective of an individual routing node in the network if no further information is known about the network as a whole.
Greedy Routing
Nearly every solution to the problem of routing in small world involves the application of greedyGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
routing. This sort of routing depends on a relative reference point by which any node in the path can choose the next node it believes is closest to the destination. That is, there must be something to be greedy about. For example, this could be geographic location, IP address, etc. In the case of Milgram's original small-world experiment, participants knew the location and occupation of the final recipient and could therefore forward messages based on those parameters.
Constructing a Reference Base
Greedy routing will not readily work when there is no obvious reference base. This can occur, for example, in overlay networkOverlay network
An overlay network is a computer network which is built on the top of another network. Nodes in the overlay can be thought of as being connected by virtual or logical links, each of which corresponds to a path, perhaps through many physical links, in the underlying network...
s where information about the destination's location in the underlying network is not available. Friend to friend networks are a particular example of this problem. In such networks, trust is ensured by the fact that you only know underlying information about nodes with whom you are already a neighbor.
One solution in this case, is to impose some sort of artificial addressing on the nodes in such a way that this addressing can be effectively used by greedy routing methods. A 2005 paper by a developer of the Freenet Project
Freenet
Freenet is a decentralized, censorship-resistant distributed data store originally designed by Ian Clarke. According to Clarke, Freenet aims to provide freedom of speech through a peer-to-peer network with strong protection of anonymity; as part of supporting its users' freedom, Freenet is free and...
discusses how this can be accomplished in friend to friend networks. Given the assumption that these networks exhibit small world properties, often as the result of real-world or acquaintance relationships, it should be possible to recover an embedded Kleinberg
Jon Kleinberg
-External links:**** Stephen Ibaraki*Yury Lifshits,...
small-world graph. This is accomplished by selecting random pairs of nodes and potentially swapping them based on an objective function that minimizes the product of all the distances between any given node and its neighbors.
An important problem involved with this solution is the possibility of local minima. This can occur if nodes are in a situation that is optimal only considering a local neighborhood, while ignoring the possibility of a higher optimality resulting from swaps with distant nodes. In the above paper, the authors proposed a simulated annealing
Simulated annealing
Simulated annealing is a generic probabilistic metaheuristic for the global optimization problem of locating a good approximation to the global optimum of a given function in a large search space. It is often used when the search space is discrete...
method where less-than-optimal swaps were made with a small probability. This probability was proportional to the value of making the switches. Another possible metaheuristic
Metaheuristic
In computer science, metaheuristic designates a computational method that optimizes a problem by iteratively trying to improve a candidate solution with regard to a given measure of quality. Metaheuristics make few or no assumptions about the problem being optimized and can search very large spaces...
optimization method is a tabu search
Tabu search
Tabu search is a mathematical optimization method, belonging to the class of trajectory based techniques. Tabu search enhances the performance of a local search method by using memory structures that describe the visited solutions: once a potential solution has been determined, it is marked as...
, which adds a memory to the swap decision. In its most simplistic form, a limited history of past swaps is remembered so that they will be excluded from the list of possible swapping nodes.
This method for constructing a reference base can also be adapted to distributed settings, where decisions can only be made at the level of individual nodes who have no knowledge of the overall network. It turns out that the only modification necessary is in the method for selecting pairs of random nodes. In a distributed setting, this is done by having each node periodically send out a random walker
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
terminating at a node to be considered for swapping.
The Kleinberg Model
The Kleinberg model of a network is effective at demonstrating the effectiveness of greedy small world routing. The model uses an n x n grid of nodes to represent a network, where each node is connected with an undirected edge to its neighbors. To give it the “small world” effect, a number of long range edges are added to the network that tend to favor nodes closer in distance rather than farther. When adding edges, the probability of connecting some random vertex to another random vertex w is proportional to
to another random vertex w is proportional to 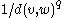 , where
, where 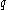 is the clustering coefficient
is the clustering coefficientClustering coefficient
In graph theory, a clustering coefficient is a measure of degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties...
.
Greedy Routing in the Kleinberg Model
It is easy to see that a greedy algorithmGreedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
, without using the long range edges, can navigate from random vertices v->w on the grid in
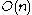 time. By following the guaranteed connections to our neighbors, we can move one unit at a time in the direction of our destination. This is also the case when the clustering component q large and the “long range” edges end up staying very close; we simply do not take advantage of the weaker ties in this model. When
time. By following the guaranteed connections to our neighbors, we can move one unit at a time in the direction of our destination. This is also the case when the clustering component q large and the “long range” edges end up staying very close; we simply do not take advantage of the weaker ties in this model. When 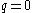 , the long range edges are uniformly connected at random which means the long range edges are “too random” to be used efficiently for decentralized search. Kleinberg has shown that the optimal clustering coefficient for this model is
, the long range edges are uniformly connected at random which means the long range edges are “too random” to be used efficiently for decentralized search. Kleinberg has shown that the optimal clustering coefficient for this model is 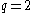 , or an inverse square distribution.
, or an inverse square distribution.To reason why this is the case, if a circle of radius r is drawn around the initial node it will have nodal density
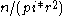 where n is the number of nodes in the circular area. As this circle gets expanded further out, the number of nodes in the given area increases proportional to
where n is the number of nodes in the circular area. As this circle gets expanded further out, the number of nodes in the given area increases proportional to 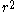 as the probability of having a random link with any node remains proportional
as the probability of having a random link with any node remains proportional  , meaning the probability of the original node having a weak tie with any node a given distance away is effectively independent of distance. Therefore, it is concluded that with
, meaning the probability of the original node having a weak tie with any node a given distance away is effectively independent of distance. Therefore, it is concluded that with 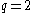 , long-range edges are evenly distributed over all distances, which is effective for letting us funnel to our final destination.
, long-range edges are evenly distributed over all distances, which is effective for letting us funnel to our final destination.

