
Skew lattice
Encyclopedia
In abstract algebra
, a skew lattice is an algebraic structure
that is a non-commutative generalization of a lattice
. While the term skew lattice can be used to refer to any non-commutative generalization of a lattice, over the past twenty years it has been used primarily as follows.
s and
and  , called meet and join, that satisfy the following dual pair of absorption laws
, called meet and join, that satisfy the following dual pair of absorption laws
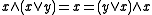 and
and 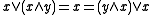 .
.
Given that and
and  are associative and idempotent, these identities are equivalent to the dualities:
are associative and idempotent, these identities are equivalent to the dualities:
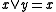 iff
iff 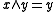 and
and  iff
iff 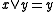 .
.
and Boolean algebra; and for others it has been the behavior of idempotents in rings
. A noncommutative lattice, generally speaking, is an algebra
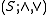 where
where  and
and  are associative, idempotent binary
are associative, idempotent binary
operations
connected by absorption identities guaranteeing that in some way dualizes
in some way dualizes  . The precise identities chosen depends upon the underlying motivation, with differing choices producing distinct varieties of algebras
. The precise identities chosen depends upon the underlying motivation, with differing choices producing distinct varieties of algebras
. Pascual Jordan, motivated by questions in quantum logic
, initiated a study of noncommutative lattices in his 1949 paper, Über Nichtkommutative Verbande, choosing the absorption identities

He referred to those algebras satisfying them as Schrägverbände. By varying or augmenting these identities, Jordan and others obtained a number of varieties of noncommutative lattices.
Beginning with Jonathan Leech's 1989 paper, Skew lattices in rings, skew lattices as defined above have been the primary objects of study. This was aided by previous results about bands. This was especially the case for many of the basic properties.
In a skew lattice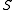 , the natural partial order is defined by
, the natural partial order is defined by 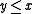 if
if 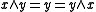 , or dually,
, or dually, 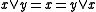 . The natural preorder
. The natural preorder
on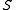 is given by
is given by 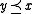 if
if 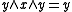 or dually
or dually  . While
. While 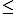 and
and 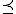 agree on lattices,
agree on lattices, 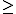 properly refines
properly refines 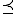 in the noncommutative case. The induced natural equivalence
in the noncommutative case. The induced natural equivalence
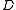 is defined by
is defined by 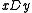 if
if 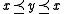 , that is,
, that is, 
and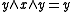 or dually,
or dually, 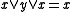 and
and 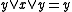 . The blocks of the partition
. The blocks of the partition  are
are
lattice ordered by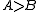 iff
iff 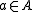 and
and 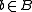 exist such that
exist such that 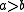 . This permits us to write Hasse diagram
. This permits us to write Hasse diagram
s of skew lattices such as the following pair:
E.g., in the diagram on the left above, that and
and  are
are 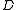 related is expressed by the dashed
related is expressed by the dashed
segment. The slanted lines reveal the natural partial order between elements of the distinct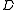 -classes. The elements
-classes. The elements 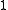 ,
,  and
and 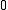 form the singleton
form the singleton 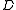 -classes.
-classes.
Rectangular Skew Lattices
Skew lattices consisting of a single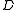 -class are called rectangular. They are characterized by the equivalent identities:
-class are called rectangular. They are characterized by the equivalent identities: 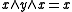 ,
, 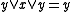 and
and 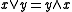 . Rectangular skew lattices are isomorphic to skew lattices having the following construction (and conversely): given nonempty
. Rectangular skew lattices are isomorphic to skew lattices having the following construction (and conversely): given nonempty
sets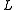 and
and 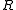 , on
, on  define
define 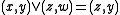 and
and  . The
. The 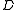 -class partition of a skew lattice
-class partition of a skew lattice 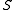 , as indicated in the above diagrams, is the unique partition of
, as indicated in the above diagrams, is the unique partition of 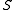 into its maximal rectangular subalgebras, Moreover,
into its maximal rectangular subalgebras, Moreover, 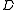 is a congruence with the induced quotient algebra
is a congruence with the induced quotient algebra 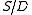 being the maximal lattice image of
being the maximal lattice image of 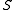 , thus making every skew lattice
, thus making every skew lattice 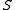 a lattice of rectangular subalgebras. This is the Clifford-McLean Theorem for skew lattices, first given for bands separately by Clifford and McLean. It is also known as the First Decomposition Theorem for skew lattices.
a lattice of rectangular subalgebras. This is the Clifford-McLean Theorem for skew lattices, first given for bands separately by Clifford and McLean. It is also known as the First Decomposition Theorem for skew lattices.
Right (left) handed skew lattices and the Kimura factorization
A skew lattice is right-handed if it satisfies the identity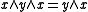 or dually,
or dually, 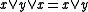 .
.
These identities essentially assert that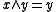 and
and 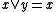 in each
in each 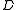 -class. Every skew lattice
-class. Every skew lattice 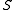 has a unique maximal right-handed image
has a unique maximal right-handed image 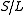 where the congruence
where the congruence  is defined by
is defined by 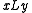 if both
if both 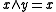 and
and 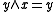 (or dually,
(or dually, 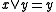 and
and 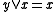 ). Likewise a skew lattice is left-handed if
). Likewise a skew lattice is left-handed if 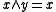 and
and  in each
in each 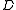 -class. Again the maximal left-handed image of a skew lattice
-class. Again the maximal left-handed image of a skew lattice 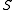 is the image
is the image 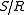 where the congruence
where the congruence 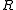 is defined in dual fashion to
is defined in dual fashion to 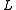 . Many examples of skew lattices are either right or left-handed. In the lattice of congruences,
. Many examples of skew lattices are either right or left-handed. In the lattice of congruences, 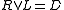 and
and 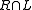 is the identity congruence
is the identity congruence 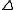 . The induced epimorphism
. The induced epimorphism 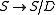 factors through both induced epimorphisms
factors through both induced epimorphisms  and
and 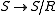 . Setting
. Setting 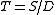 , the homomorphism
, the homomorphism 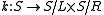 defined by
defined by 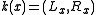 , induces an isomorphism
, induces an isomorphism 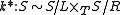 . This is the Kimura factorization of
. This is the Kimura factorization of 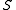 into a fibred product of its maximal right and left-handed images.
into a fibred product of its maximal right and left-handed images.
Like the Clifford-McLean Theorem, Kimura factorization (or the Second Decomposition Theorem for skew lattices) was first given for regular bands (that satisfy the middle absorption
identity, ). Indeed both
). Indeed both  and
and  are regular band operations. The above symbols
are regular band operations. The above symbols 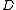 ,
, 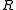 and
and 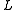 come, of course, from basic semigroup theory.
come, of course, from basic semigroup theory.
For more details on the basic properties of a skew lattice please read and .
more.
Symmetric Skew Lattices
A skew lattice S is symmetric if for any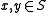 ,
, 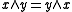 iff
iff 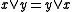 . Occurrences of commutation are thus unambiguous for such skew lattices, with subsets of pairwise commuting elements generating commutative subalgebras, i.e, sublattices. ( This is not true for skew lattices in general.) Equational bases for this subvariety, first given by Spinks are:
. Occurrences of commutation are thus unambiguous for such skew lattices, with subsets of pairwise commuting elements generating commutative subalgebras, i.e, sublattices. ( This is not true for skew lattices in general.) Equational bases for this subvariety, first given by Spinks are:
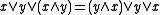 and
and 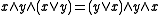 .
.
A lattice section of a skew lattice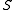 is a sublattice
is a sublattice 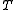 of
of 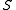 meeting each
meeting each 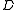 -class of
-class of 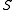 at a single element.
at a single element. 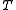 is thus an internal copy of the lattice
is thus an internal copy of the lattice 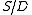 with the composition
with the composition 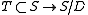 being an isomorphism. All symmetric skew lattices for which |S/D| \leq \aleph_0 , admit a lattice section. Symmetric or not, having a lattice section
being an isomorphism. All symmetric skew lattices for which |S/D| \leq \aleph_0 , admit a lattice section. Symmetric or not, having a lattice section 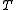 guarantees that
guarantees that 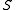 also has internal copies of
also has internal copies of 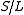 and
and 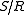 given respectively by
given respectively by 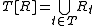 and
and 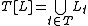 , where
, where 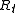 and
and 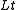 are the
are the  and
and 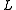 congruence classes of
congruence classes of  in
in 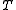 . Thus
. Thus 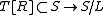 and
and 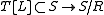 are isomorphisms (See ). This leads to a commuting diagram of embedding dualizing the preceding Kimura diagram.
are isomorphisms (See ). This leads to a commuting diagram of embedding dualizing the preceding Kimura diagram.
Cancellative Skew Lattices
A skew lattice is cancellative if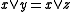 and
and 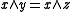 implies
implies 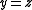 and likewise
and likewise 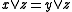 and
and 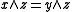 implies
implies 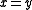 . Cancellatice skew lattices are symmetric and can be shown to form a variety. Unlike lattices, they need not be distributive, and conversely.
. Cancellatice skew lattices are symmetric and can be shown to form a variety. Unlike lattices, they need not be distributive, and conversely.
Distributive Skew Lattices
Distributive skew lattices are determined by the identities:
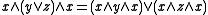 (D1 )
(D1 )
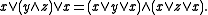 (D’1 )
(D’1 )
Unlike lattices, (D1 ) and (D‘1 ) are not equivalent in general for skew lattices, but they are for symmetric skew lattices. (See,,.) The condition (D1 ) can be strengthened to (D2 ) in which case (D‘1 ) is a consequence. A skew lattice
(D2 ) in which case (D‘1 ) is a consequence. A skew lattice 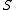 satisfies both (D2) and its dual,
satisfies both (D2) and its dual, 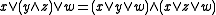 , if and only if it factors as the product of a distributive lattice and a rectangular skew lattice. In this latter case (D2 ) can be strengthened to
, if and only if it factors as the product of a distributive lattice and a rectangular skew lattice. In this latter case (D2 ) can be strengthened to 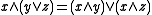 and
and 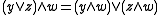 . (D3 )
. (D3 )
On its own, (D3 ) is equivalent to (D2 ) when symmetry is added. (See.) We thus have six subvarieties of skew lattices determined respectively by (D1), (D2), (D3) and their duals.
Normal Skew Lattices
As seen above, and
and  satisfy the identity
satisfy the identity  . Bands satisfying the stronger identity,
. Bands satisfying the stronger identity, 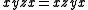 , are called normal. A skew lattice is normal skew if it satisfies
, are called normal. A skew lattice is normal skew if it satisfies
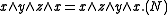
For each element a in a normal skew lattice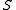 , the set
, the set  defined by {
defined by { 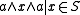 } or equivalently {
} or equivalently {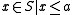 } is a sublattice of
} is a sublattice of  , and conversely. (Thus normal skew lattices have also been called local lattices.) When both
, and conversely. (Thus normal skew lattices have also been called local lattices.) When both  and
and  are normal,
are normal, 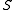 splits isomorphically into a product
splits isomorphically into a product 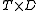 of a lattice
of a lattice 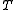 and a rectangular skew lattice
and a rectangular skew lattice 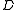 , and conversely. Thus both normal skew lattices and split skew lattices form varieties. Returning to distribution,
, and conversely. Thus both normal skew lattices and split skew lattices form varieties. Returning to distribution,  so that
so that 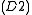 characterizes the variety of distributive, normal skew lattices, and (D3) characterizes the variety of symmetric, distributive, normal skew lattices.
characterizes the variety of distributive, normal skew lattices, and (D3) characterizes the variety of symmetric, distributive, normal skew lattices.
Categorical Skew Lattices
A skew lattice is categorical if nonempty composites of coset bijections are coset bijections. Categorical skew lattices form a variety. Skew lattices in rings and normal skew lattices are examples
of algebras on this variety. Let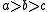 with
with 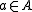 ,
, 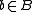 and
and 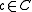 ,
,  be the coset bijection from
be the coset bijection from 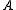 to
to 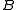 taking
taking  to
to 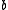 ,
,  be the coset bijection from
be the coset bijection from 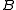 to
to 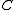 taking
taking 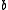 to
to  and finally
and finally 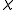 be the coset bijection from
be the coset bijection from 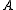 to
to 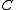 taking
taking  to
to  . A skew lattice
. A skew lattice 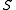 is categorical if one always has the equality
is categorical if one always has the equality 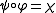 , ie. , if the
, ie. , if the
composite partial bijection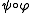 if nonempty is a coset bijection from a
if nonempty is a coset bijection from a 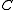 -coset of
-coset of 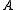 to an
to an 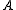 -coset
-coset
of . That is
. That is 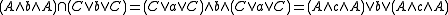 .
.
All distributive skew lattices are categorical. Though symmetric skew lattices might not be. In a sense they reveal the independence between the properties of symmetry and distributivity.
For more details on these and other subvarieties of skew lattices please read and .
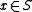 ,
, 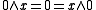 or, dually,
or, dually, 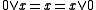 . (0)
. (0)
A Boolean skew lattice is a symmetric, distributive normal skew lattice with 0, , such that
, such that  is a Boolean lattice for each
is a Boolean lattice for each 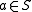 . Given such skew lattice S , a difference operator \ is defined on by x\ y =
. Given such skew lattice S , a difference operator \ is defined on by x\ y = 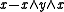 where the latter is evaluated in the Boolean lattice
where the latter is evaluated in the Boolean lattice 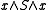 . In the presence of (D3) and (0), \ is characterized by the identities:
. In the presence of (D3) and (0), \ is characterized by the identities:
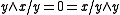 and
and 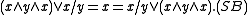
One thus has a variety of skew Boolean algebras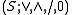 characterized by identities (D3), (0) and (S B). A primitive skew Boolean algebra consists of 0 and a single non-0 D-class. Thus it is the result of adjoining a 0 to a rectangular skew lattice D via (0) with
characterized by identities (D3), (0) and (S B). A primitive skew Boolean algebra consists of 0 and a single non-0 D-class. Thus it is the result of adjoining a 0 to a rectangular skew lattice D via (0) with 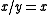 , if
, if 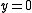
and otherwise. Every skew Boolean algebra is a subdirect product of primitive algebras. Skew Boolean algebras play an important role in the study of discriminator varieties and other generalizations in universal algebra of Boolean behavior. For more details on skew Boolean algebras see,,,,, ,,, and.
otherwise. Every skew Boolean algebra is a subdirect product of primitive algebras. Skew Boolean algebras play an important role in the study of discriminator varieties and other generalizations in universal algebra of Boolean behavior. For more details on skew Boolean algebras see,,,,, ,,, and.
 be a Ring
be a Ring
and let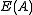 denote the set of all Idempotents in
denote the set of all Idempotents in 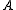 . For all
. For all  set
set 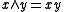 and
and 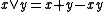 .
.
Clearly but also
but also  is associative. If a subset
is associative. If a subset 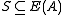 is closed under
is closed under  and
and  , then
, then 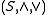 is a distributive, cancellative skew lattice. To find such skew lattices in
is a distributive, cancellative skew lattice. To find such skew lattices in 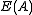 one looks at bands in
one looks at bands in 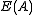 , especially the ones that are maximal with respect to some constraint. In fact, every multiplicative band in
, especially the ones that are maximal with respect to some constraint. In fact, every multiplicative band in  that is maximal with respect to being right regular (= ) is also closed under
that is maximal with respect to being right regular (= ) is also closed under  and so forms a right-handed skew lattice. In general, every right regular band in
and so forms a right-handed skew lattice. In general, every right regular band in 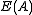 generates a right-handed skew lattice in
generates a right-handed skew lattice in 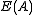 . Dual remarks also hold for left regular bands (bands satisfying the identity
. Dual remarks also hold for left regular bands (bands satisfying the identity  ) in
) in  . Maximal regular bands need not to be closed under
. Maximal regular bands need not to be closed under  as defined; counterexamples are easily found using multiplicative rectangular bands. These cases are closed, however, under the cubic variant of
as defined; counterexamples are easily found using multiplicative rectangular bands. These cases are closed, however, under the cubic variant of  defined by
defined by 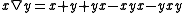 since in these cases
since in these cases 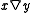 reduces to
reduces to 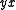 to give the dual rectangular band. By replacing the condition of regularity by normality
to give the dual rectangular band. By replacing the condition of regularity by normality 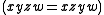 , every maximal normal multiplicative band
, every maximal normal multiplicative band 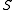 in
in 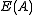 is also closed under
is also closed under 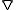 with
with 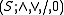 , where
, where 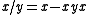 , forms a Boolean skew lattice. When
, forms a Boolean skew lattice. When 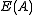 itself is closed under multiplication, then it is a normal band and thus forms a Boolean skew lattice. In fact, any skew Boolean algebra can be embedded into such an algebra. (See.) When A has a multiplicative identity
itself is closed under multiplication, then it is a normal band and thus forms a Boolean skew lattice. In fact, any skew Boolean algebra can be embedded into such an algebra. (See.) When A has a multiplicative identity 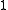 , the condition that
, the condition that 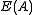 is multiplicatively closed is well-known to imply that
is multiplicatively closed is well-known to imply that 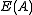 forms a Boolean algebra. Skew lattices in rings continue to be a good source of examples and motivation. For more details read .
forms a Boolean algebra. Skew lattices in rings continue to be a good source of examples and motivation. For more details read .
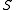 with
with 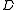 -classes
-classes 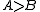 in
in 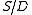 , then for any
, then for any 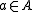 and
and  , the subsets
, the subsets
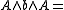 {
{ }
} 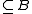 and
and 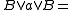 {
{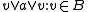 }
} 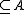
are called, respectively, cosets of A in B and cosets of B in A. These cosets partition B and A with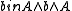 and
and  . Cosets are always rectangular subalgebras in their
. Cosets are always rectangular subalgebras in their 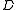 -classes. What is more, the partial order
-classes. What is more, the partial order 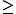 induces a coset bijection
induces a coset bijection 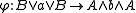 defined by:
defined by:
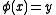 iff
iff 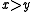 , for
, for  and
and 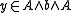 .
.
Collectively, coset bijections describe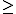 between the subsets
between the subsets 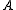 and
and 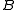 . They also determine
. They also determine  and
and  for pairs of elements from distinct
for pairs of elements from distinct 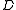 -classes. Indeed, given
-classes. Indeed, given 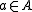 and
and 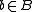 , let
, let 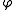 be the
be the
cost bijection between the cosets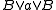 in
in 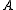 and
and 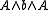 in
in  . Then:
. Then:
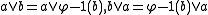 and
and 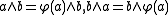 .
.
In general, given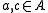 and
and 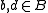 with
with 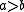 and
and 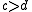 , then
, then 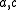 belong to a common
belong to a common 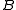 - coset in
- coset in 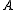 and
and 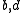 belong to a common
belong to a common 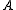 -coset in
-coset in 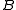 if and only if
if and only if 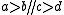 . Thus each coset bijection is, in some sense, a maximal collection of mutually parallel pairs
. Thus each coset bijection is, in some sense, a maximal collection of mutually parallel pairs 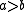 .
.
Every primitive skew lattice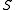 factors as the fibred product of its maximal left and right- handed primitive images
factors as the fibred product of its maximal left and right- handed primitive images 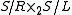 . Right-handed primitive skew lattices are constructed as follows. Let
. Right-handed primitive skew lattices are constructed as follows. Let 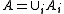 and
and 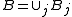 be partitions of disjoint nonempty sets
be partitions of disjoint nonempty sets 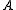 and
and 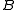 , where all
, where all 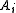 and
and 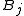 share a common size. For each pair
share a common size. For each pair 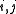 pick a fixed bijection
pick a fixed bijection 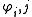 from
from 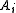 onto
onto 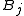 . On
. On 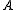 and
and 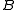 separately set
separately set 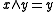 and
and 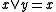 ; but given
; but given  and
and  , set
, set
 and
and 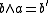
where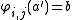 and
and 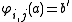 with
with 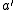 belonging to the cell
belonging to the cell 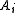 of
of  and
and 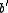 belonging to the cell
belonging to the cell  of
of 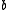 . The various
. The various 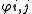 are the coset bijections. This is illustrated in the following partial Hasse diagram where
are the coset bijections. This is illustrated in the following partial Hasse diagram where 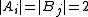 and the arrows indicate the
and the arrows indicate the 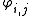 -outputs and
-outputs and 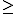 from
from 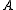 and
and 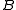 .
.
One constructs left-handed primitive skew lattices in dual fashion. All right [left] handed primitive skew lattices can be constructed in this fashion. (See Section 1.)
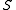 is covered by its maximal primitive skew lattices: given comparable
is covered by its maximal primitive skew lattices: given comparable 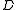 -classes
-classes 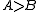 in
in 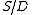 ,
, 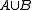 forms a maximal primitive subalgebra of
forms a maximal primitive subalgebra of 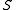 and every
and every 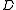 -class in
-class in 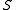 lies in such a subalgebra. The coset structures on these primitive subalgebras combine to determine the outcomes
lies in such a subalgebra. The coset structures on these primitive subalgebras combine to determine the outcomes  and
and 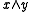 at least when
at least when  and
and 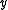 are comparable under
are comparable under 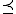 . It turns out that
. It turns out that 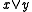 and
and 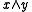 are determined in general by cosets and their bijections, although in
are determined in general by cosets and their bijections, although in
a slightly less direct manner than the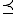 -comparable case. In particular, given two incomparable D-classes A and B with join D-class J and meet D-class
-comparable case. In particular, given two incomparable D-classes A and B with join D-class J and meet D-class 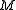 in
in  , interesting connections arise between the two coset decompositions of J (or M) with respect to A and B. (See Section 3.)
, interesting connections arise between the two coset decompositions of J (or M) with respect to A and B. (See Section 3.)
Thus a skew lattice may be viewed as a coset atlas of rectangular skew lattices placed on the vertices of a lattice and coset bijections between them, the latter seen as partial isomorphisms
between the rectangular algebras with each coset bijection determining a corresponding pair of cosets. This perspective gives, in essence, the Hasse diagram of the skew lattice, which is easily
drawn in cases of relatively small order. (See the diagrams in Section 3 above.) Given a chain of D-classes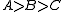 in
in 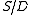 , one has three sets of coset bijections: from A to B, from B to C and from A to C. In general, given coset bijections
, one has three sets of coset bijections: from A to B, from B to C and from A to C. In general, given coset bijections  and
and 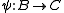 , the composition of partial bijections
, the composition of partial bijections 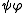 could be empty. If it is not, then a unique coset bijection
could be empty. If it is not, then a unique coset bijection 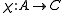 exists such that
exists such that 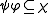 . (Again,
. (Again,  is a bijection between a pair of cosets in
is a bijection between a pair of cosets in  and
and 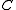 .) This inclusion can be strict. It is always an equality (given
.) This inclusion can be strict. It is always an equality (given 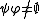 ) on a given skew lattice S precisely when S is categorical. In this case, by including the identity maps on each rectangular D-class and adjoining empty bijections between properly comparable D-classes, one has a category of rectangular algebras and coset bijections between them. The simple examples in Section 3 are categorical.
) on a given skew lattice S precisely when S is categorical. In this case, by including the identity maps on each rectangular D-class and adjoining empty bijections between properly comparable D-classes, one has a category of rectangular algebras and coset bijections between them. The simple examples in Section 3 are categorical.
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, a skew lattice is an algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
that is a non-commutative generalization of a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
. While the term skew lattice can be used to refer to any non-commutative generalization of a lattice, over the past twenty years it has been used primarily as follows.
Definition
A skew lattice is a set S equipped with two associative, idempotent binary operationBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
s
 and
and  , called meet and join, that satisfy the following dual pair of absorption laws
, called meet and join, that satisfy the following dual pair of absorption laws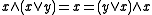 and
and 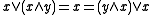 .
.Given that
 and
and  are associative and idempotent, these identities are equivalent to the dualities:
are associative and idempotent, these identities are equivalent to the dualities: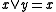 iff
iff 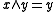 and
and  iff
iff 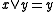 .
. Historical background
For over 60 years, noncommutative variations of lattices have been studied with differing motivations. For some the motivation has been an interest in the conceptual boundaries of lattice theory; for others it was a search for noncommutative forms of logicMathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
and Boolean algebra; and for others it has been the behavior of idempotents in rings
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
. A noncommutative lattice, generally speaking, is an algebra
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
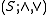 where
where  and
and  are associative, idempotent binary
are associative, idempotent binaryBinary operation
In mathematics, a binary operation is a calculation involving two operands, in other words, an operation whose arity is two. Examples include the familiar arithmetic operations of addition, subtraction, multiplication and division....
operations
Operation (mathematics)
The general operation as explained on this page should not be confused with the more specific operators on vector spaces. For a notion in elementary mathematics, see arithmetic operation....
connected by absorption identities guaranteeing that
 in some way dualizes
in some way dualizes  . The precise identities chosen depends upon the underlying motivation, with differing choices producing distinct varieties of algebras
. The precise identities chosen depends upon the underlying motivation, with differing choices producing distinct varieties of algebrasVariety (universal algebra)
In mathematics, specifically universal algebra, a variety of algebras is the class of all algebraic structures of a given signature satisfying a given set of identities. Equivalently, a variety is a class of algebraic structures of the same signature which is closed under the taking of homomorphic...
. Pascual Jordan, motivated by questions in quantum logic
Quantum logic
In quantum mechanics, quantum logic is a set of rules for reasoning about propositions which takes the principles of quantum theory into account...
, initiated a study of noncommutative lattices in his 1949 paper, Über Nichtkommutative Verbande, choosing the absorption identities

He referred to those algebras satisfying them as Schrägverbände. By varying or augmenting these identities, Jordan and others obtained a number of varieties of noncommutative lattices.
Beginning with Jonathan Leech's 1989 paper, Skew lattices in rings, skew lattices as defined above have been the primary objects of study. This was aided by previous results about bands. This was especially the case for many of the basic properties.
Basic properties
Natural partial order and natural quasiorderIn a skew lattice
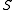 , the natural partial order is defined by
, the natural partial order is defined by 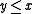 if
if 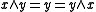 , or dually,
, or dually, 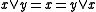 . The natural preorder
. The natural preorderPreorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
on
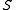 is given by
is given by 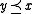 if
if 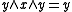 or dually
or dually  . While
. While 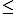 and
and 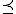 agree on lattices,
agree on lattices, 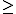 properly refines
properly refines 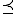 in the noncommutative case. The induced natural equivalence
in the noncommutative case. The induced natural equivalenceEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
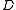 is defined by
is defined by 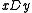 if
if 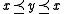 , that is,
, that is, 
and
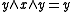 or dually,
or dually, 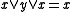 and
and 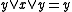 . The blocks of the partition
. The blocks of the partition  are
arelattice ordered by
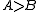 iff
iff 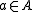 and
and 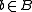 exist such that
exist such that 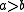 . This permits us to write Hasse diagram
. This permits us to write Hasse diagramHasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
s of skew lattices such as the following pair:
E.g., in the diagram on the left above, that
 and
and  are
are 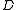 related is expressed by the dashed
related is expressed by the dashedsegment. The slanted lines reveal the natural partial order between elements of the distinct
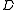 -classes. The elements
-classes. The elements 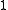 ,
,  and
and 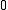 form the singleton
form the singleton 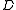 -classes.
-classes.Rectangular Skew Lattices
Skew lattices consisting of a single
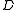 -class are called rectangular. They are characterized by the equivalent identities:
-class are called rectangular. They are characterized by the equivalent identities: 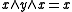 ,
, 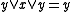 and
and 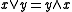 . Rectangular skew lattices are isomorphic to skew lattices having the following construction (and conversely): given nonempty
. Rectangular skew lattices are isomorphic to skew lattices having the following construction (and conversely): given nonemptysets
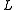 and
and 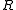 , on
, on  define
define 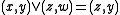 and
and  . The
. The  -class partition of a skew lattice
-class partition of a skew lattice 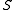 , as indicated in the above diagrams, is the unique partition of
, as indicated in the above diagrams, is the unique partition of 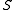 into its maximal rectangular subalgebras, Moreover,
into its maximal rectangular subalgebras, Moreover, 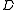 is a congruence with the induced quotient algebra
is a congruence with the induced quotient algebra 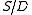 being the maximal lattice image of
being the maximal lattice image of 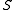 , thus making every skew lattice
, thus making every skew lattice 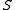 a lattice of rectangular subalgebras. This is the Clifford-McLean Theorem for skew lattices, first given for bands separately by Clifford and McLean. It is also known as the First Decomposition Theorem for skew lattices.
a lattice of rectangular subalgebras. This is the Clifford-McLean Theorem for skew lattices, first given for bands separately by Clifford and McLean. It is also known as the First Decomposition Theorem for skew lattices.Right (left) handed skew lattices and the Kimura factorization
A skew lattice is right-handed if it satisfies the identity
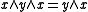 or dually,
or dually, 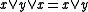 .
.These identities essentially assert that
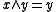 and
and 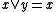 in each
in each 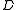 -class. Every skew lattice
-class. Every skew lattice 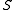 has a unique maximal right-handed image
has a unique maximal right-handed image 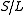 where the congruence
where the congruence  is defined by
is defined by 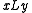 if both
if both 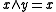 and
and 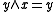 (or dually,
(or dually, 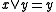 and
and 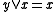 ). Likewise a skew lattice is left-handed if
). Likewise a skew lattice is left-handed if 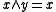 and
and  in each
in each 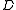 -class. Again the maximal left-handed image of a skew lattice
-class. Again the maximal left-handed image of a skew lattice 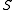 is the image
is the image 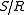 where the congruence
where the congruence 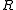 is defined in dual fashion to
is defined in dual fashion to 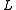 . Many examples of skew lattices are either right or left-handed. In the lattice of congruences,
. Many examples of skew lattices are either right or left-handed. In the lattice of congruences, 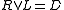 and
and 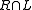 is the identity congruence
is the identity congruence 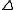 . The induced epimorphism
. The induced epimorphism 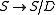 factors through both induced epimorphisms
factors through both induced epimorphisms  and
and 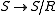 . Setting
. Setting 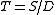 , the homomorphism
, the homomorphism 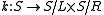 defined by
defined by 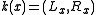 , induces an isomorphism
, induces an isomorphism 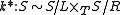 . This is the Kimura factorization of
. This is the Kimura factorization of 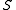 into a fibred product of its maximal right and left-handed images.
into a fibred product of its maximal right and left-handed images.Like the Clifford-McLean Theorem, Kimura factorization (or the Second Decomposition Theorem for skew lattices) was first given for regular bands (that satisfy the middle absorption
identity,
 ). Indeed both
). Indeed both  and
and  are regular band operations. The above symbols
are regular band operations. The above symbols 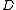 ,
, 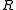 and
and 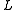 come, of course, from basic semigroup theory.
come, of course, from basic semigroup theory.For more details on the basic properties of a skew lattice please read and .
Subvarieties of skew lattices
Skew lattices form a variety. Rectangular skew lattices, left-handed and right-handed skew lattices all form subvarieties that are central to the basic structure theory of skew lattices. Here are severalmore.
Symmetric Skew Lattices
A skew lattice S is symmetric if for any
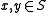 ,
, 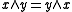 iff
iff 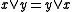 . Occurrences of commutation are thus unambiguous for such skew lattices, with subsets of pairwise commuting elements generating commutative subalgebras, i.e, sublattices. ( This is not true for skew lattices in general.) Equational bases for this subvariety, first given by Spinks are:
. Occurrences of commutation are thus unambiguous for such skew lattices, with subsets of pairwise commuting elements generating commutative subalgebras, i.e, sublattices. ( This is not true for skew lattices in general.) Equational bases for this subvariety, first given by Spinks are: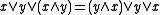 and
and 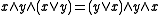 .
.A lattice section of a skew lattice
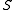 is a sublattice
is a sublattice 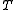 of
of 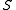 meeting each
meeting each 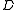 -class of
-class of 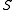 at a single element.
at a single element. 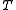 is thus an internal copy of the lattice
is thus an internal copy of the lattice 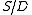 with the composition
with the composition 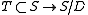 being an isomorphism. All symmetric skew lattices for which |S/D| \leq \aleph_0 , admit a lattice section. Symmetric or not, having a lattice section
being an isomorphism. All symmetric skew lattices for which |S/D| \leq \aleph_0 , admit a lattice section. Symmetric or not, having a lattice section 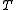 guarantees that
guarantees that 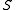 also has internal copies of
also has internal copies of 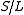 and
and 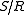 given respectively by
given respectively by 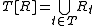 and
and 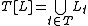 , where
, where 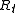 and
and 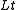 are the
are the  and
and 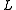 congruence classes of
congruence classes of  in
in 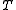 . Thus
. Thus 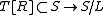 and
and 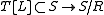 are isomorphisms (See ). This leads to a commuting diagram of embedding dualizing the preceding Kimura diagram.
are isomorphisms (See ). This leads to a commuting diagram of embedding dualizing the preceding Kimura diagram.Cancellative Skew Lattices
A skew lattice is cancellative if
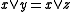 and
and 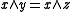 implies
implies 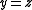 and likewise
and likewise 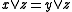 and
and 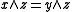 implies
implies 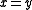 . Cancellatice skew lattices are symmetric and can be shown to form a variety. Unlike lattices, they need not be distributive, and conversely.
. Cancellatice skew lattices are symmetric and can be shown to form a variety. Unlike lattices, they need not be distributive, and conversely.Distributive Skew Lattices
Distributive skew lattices are determined by the identities:
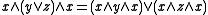 (D1 )
(D1 )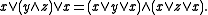 (D’1 )
(D’1 )Unlike lattices, (D1 ) and (D‘1 ) are not equivalent in general for skew lattices, but they are for symmetric skew lattices. (See,,.) The condition (D1 ) can be strengthened to
 (D2 ) in which case (D‘1 ) is a consequence. A skew lattice
(D2 ) in which case (D‘1 ) is a consequence. A skew lattice 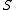 satisfies both (D2) and its dual,
satisfies both (D2) and its dual, 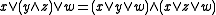 , if and only if it factors as the product of a distributive lattice and a rectangular skew lattice. In this latter case (D2 ) can be strengthened to
, if and only if it factors as the product of a distributive lattice and a rectangular skew lattice. In this latter case (D2 ) can be strengthened to 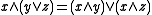 and
and 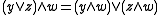 . (D3 )
. (D3 )On its own, (D3 ) is equivalent to (D2 ) when symmetry is added. (See.) We thus have six subvarieties of skew lattices determined respectively by (D1), (D2), (D3) and their duals.
Normal Skew Lattices
As seen above,
 and
and  satisfy the identity
satisfy the identity  . Bands satisfying the stronger identity,
. Bands satisfying the stronger identity, 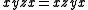 , are called normal. A skew lattice is normal skew if it satisfies
, are called normal. A skew lattice is normal skew if it satisfies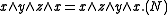
For each element a in a normal skew lattice
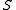 , the set
, the set  defined by {
defined by { 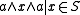 } or equivalently {
} or equivalently {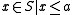 } is a sublattice of
} is a sublattice of  , and conversely. (Thus normal skew lattices have also been called local lattices.) When both
, and conversely. (Thus normal skew lattices have also been called local lattices.) When both  and
and  are normal,
are normal, 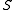 splits isomorphically into a product
splits isomorphically into a product 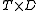 of a lattice
of a lattice 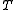 and a rectangular skew lattice
and a rectangular skew lattice 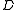 , and conversely. Thus both normal skew lattices and split skew lattices form varieties. Returning to distribution,
, and conversely. Thus both normal skew lattices and split skew lattices form varieties. Returning to distribution,  so that
so that 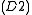 characterizes the variety of distributive, normal skew lattices, and (D3) characterizes the variety of symmetric, distributive, normal skew lattices.
characterizes the variety of distributive, normal skew lattices, and (D3) characterizes the variety of symmetric, distributive, normal skew lattices.Categorical Skew Lattices
A skew lattice is categorical if nonempty composites of coset bijections are coset bijections. Categorical skew lattices form a variety. Skew lattices in rings and normal skew lattices are examples
of algebras on this variety. Let
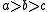 with
with 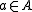 ,
, 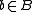 and
and 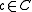 ,
,  be the coset bijection from
be the coset bijection from 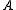 to
to 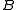 taking
taking  to
to 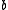 ,
,  be the coset bijection from
be the coset bijection from 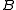 to
to 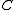 taking
taking 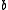 to
to  and finally
and finally 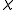 be the coset bijection from
be the coset bijection from 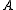 to
to 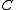 taking
taking  to
to  . A skew lattice
. A skew lattice 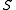 is categorical if one always has the equality
is categorical if one always has the equality 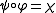 , ie. , if the
, ie. , if thecomposite partial bijection
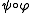 if nonempty is a coset bijection from a
if nonempty is a coset bijection from a 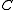 -coset of
-coset of 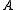 to an
to an 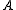 -coset
-cosetof
 . That is
. That is 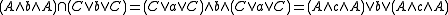 .
.All distributive skew lattices are categorical. Though symmetric skew lattices might not be. In a sense they reveal the independence between the properties of symmetry and distributivity.
For more details on these and other subvarieties of skew lattices please read and .
Skew boolean algebras
A zero element in a skew lattice S is an element 0 of S such that for all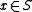 ,
, 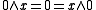 or, dually,
or, dually, 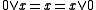 . (0)
. (0)A Boolean skew lattice is a symmetric, distributive normal skew lattice with 0,
 , such that
, such that  is a Boolean lattice for each
is a Boolean lattice for each 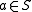 . Given such skew lattice S , a difference operator \ is defined on by x\ y =
. Given such skew lattice S , a difference operator \ is defined on by x\ y = 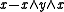 where the latter is evaluated in the Boolean lattice
where the latter is evaluated in the Boolean lattice 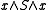 . In the presence of (D3) and (0), \ is characterized by the identities:
. In the presence of (D3) and (0), \ is characterized by the identities: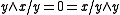 and
and 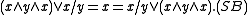
One thus has a variety of skew Boolean algebras
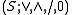 characterized by identities (D3), (0) and (S B). A primitive skew Boolean algebra consists of 0 and a single non-0 D-class. Thus it is the result of adjoining a 0 to a rectangular skew lattice D via (0) with
characterized by identities (D3), (0) and (S B). A primitive skew Boolean algebra consists of 0 and a single non-0 D-class. Thus it is the result of adjoining a 0 to a rectangular skew lattice D via (0) with 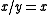 , if
, if 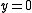
and
 otherwise. Every skew Boolean algebra is a subdirect product of primitive algebras. Skew Boolean algebras play an important role in the study of discriminator varieties and other generalizations in universal algebra of Boolean behavior. For more details on skew Boolean algebras see,,,,, ,,, and.
otherwise. Every skew Boolean algebra is a subdirect product of primitive algebras. Skew Boolean algebras play an important role in the study of discriminator varieties and other generalizations in universal algebra of Boolean behavior. For more details on skew Boolean algebras see,,,,, ,,, and.Skew lattices in rings
Let be a Ring
be a RingRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
and let
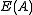 denote the set of all Idempotents in
denote the set of all Idempotents in 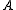 . For all
. For all  set
set 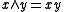 and
and 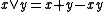 .
.Clearly
 but also
but also  is associative. If a subset
is associative. If a subset 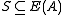 is closed under
is closed under  and
and  , then
, then 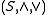 is a distributive, cancellative skew lattice. To find such skew lattices in
is a distributive, cancellative skew lattice. To find such skew lattices in 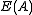 one looks at bands in
one looks at bands in 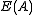 , especially the ones that are maximal with respect to some constraint. In fact, every multiplicative band in
, especially the ones that are maximal with respect to some constraint. In fact, every multiplicative band in 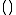 that is maximal with respect to being right regular (= ) is also closed under
that is maximal with respect to being right regular (= ) is also closed under  and so forms a right-handed skew lattice. In general, every right regular band in
and so forms a right-handed skew lattice. In general, every right regular band in 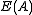 generates a right-handed skew lattice in
generates a right-handed skew lattice in 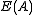 . Dual remarks also hold for left regular bands (bands satisfying the identity
. Dual remarks also hold for left regular bands (bands satisfying the identity  ) in
) in  . Maximal regular bands need not to be closed under
. Maximal regular bands need not to be closed under  as defined; counterexamples are easily found using multiplicative rectangular bands. These cases are closed, however, under the cubic variant of
as defined; counterexamples are easily found using multiplicative rectangular bands. These cases are closed, however, under the cubic variant of  defined by
defined by 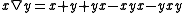 since in these cases
since in these cases 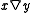 reduces to
reduces to 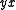 to give the dual rectangular band. By replacing the condition of regularity by normality
to give the dual rectangular band. By replacing the condition of regularity by normality 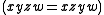 , every maximal normal multiplicative band
, every maximal normal multiplicative band 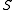 in
in 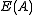 is also closed under
is also closed under 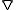 with
with 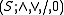 , where
, where 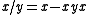 , forms a Boolean skew lattice. When
, forms a Boolean skew lattice. When 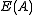 itself is closed under multiplication, then it is a normal band and thus forms a Boolean skew lattice. In fact, any skew Boolean algebra can be embedded into such an algebra. (See.) When A has a multiplicative identity
itself is closed under multiplication, then it is a normal band and thus forms a Boolean skew lattice. In fact, any skew Boolean algebra can be embedded into such an algebra. (See.) When A has a multiplicative identity 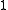 , the condition that
, the condition that 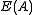 is multiplicatively closed is well-known to imply that
is multiplicatively closed is well-known to imply that 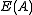 forms a Boolean algebra. Skew lattices in rings continue to be a good source of examples and motivation. For more details read .
forms a Boolean algebra. Skew lattices in rings continue to be a good source of examples and motivation. For more details read .Primitive skew lattices
Skew lattices consisting of exactly two D-classes are called primitive skew lattices. Given such a skew lattice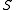 with
with 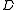 -classes
-classes 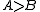 in
in 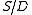 , then for any
, then for any 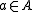 and
and  , the subsets
, the subsets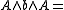 {
{ }
} 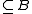 and
and 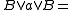 {
{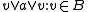 }
} 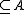
are called, respectively, cosets of A in B and cosets of B in A. These cosets partition B and A with
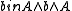 and
and  . Cosets are always rectangular subalgebras in their
. Cosets are always rectangular subalgebras in their 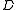 -classes. What is more, the partial order
-classes. What is more, the partial order 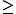 induces a coset bijection
induces a coset bijection 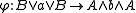 defined by:
defined by: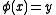 iff
iff 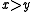 , for
, for  and
and 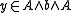 .
.Collectively, coset bijections describe
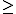 between the subsets
between the subsets 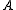 and
and 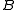 . They also determine
. They also determine  and
and  for pairs of elements from distinct
for pairs of elements from distinct 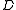 -classes. Indeed, given
-classes. Indeed, given 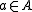 and
and 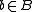 , let
, let 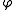 be the
be thecost bijection between the cosets
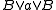 in
in 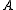 and
and 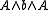 in
in  . Then:
. Then: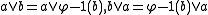 and
and 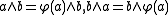 .
.In general, given
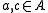 and
and 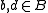 with
with 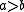 and
and 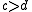 , then
, then 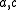 belong to a common
belong to a common 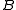 - coset in
- coset in 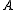 and
and 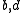 belong to a common
belong to a common 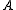 -coset in
-coset in 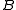 if and only if
if and only if 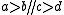 . Thus each coset bijection is, in some sense, a maximal collection of mutually parallel pairs
. Thus each coset bijection is, in some sense, a maximal collection of mutually parallel pairs 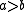 .
.Every primitive skew lattice
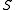 factors as the fibred product of its maximal left and right- handed primitive images
factors as the fibred product of its maximal left and right- handed primitive images 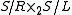 . Right-handed primitive skew lattices are constructed as follows. Let
. Right-handed primitive skew lattices are constructed as follows. Let 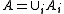 and
and 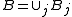 be partitions of disjoint nonempty sets
be partitions of disjoint nonempty sets 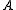 and
and 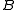 , where all
, where all 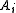 and
and 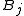 share a common size. For each pair
share a common size. For each pair 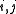 pick a fixed bijection
pick a fixed bijection 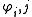 from
from 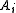 onto
onto 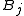 . On
. On 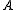 and
and 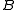 separately set
separately set 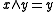 and
and 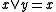 ; but given
; but given  and
and  , set
, set and
and 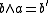
where
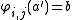 and
and 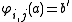 with
with 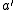 belonging to the cell
belonging to the cell 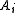 of
of  and
and 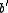 belonging to the cell
belonging to the cell  of
of 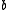 . The various
. The various 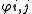 are the coset bijections. This is illustrated in the following partial Hasse diagram where
are the coset bijections. This is illustrated in the following partial Hasse diagram where 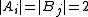 and the arrows indicate the
and the arrows indicate the 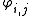 -outputs and
-outputs and 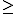 from
from 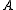 and
and 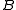 .
.One constructs left-handed primitive skew lattices in dual fashion. All right [left] handed primitive skew lattices can be constructed in this fashion. (See Section 1.)
The coset structure of skew lattices
A nonrectangular skew lattice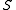 is covered by its maximal primitive skew lattices: given comparable
is covered by its maximal primitive skew lattices: given comparable 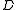 -classes
-classes 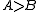 in
in 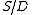 ,
, 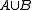 forms a maximal primitive subalgebra of
forms a maximal primitive subalgebra of 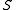 and every
and every 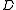 -class in
-class in 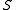 lies in such a subalgebra. The coset structures on these primitive subalgebras combine to determine the outcomes
lies in such a subalgebra. The coset structures on these primitive subalgebras combine to determine the outcomes  and
and 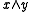 at least when
at least when  and
and 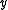 are comparable under
are comparable under 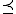 . It turns out that
. It turns out that 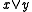 and
and 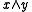 are determined in general by cosets and their bijections, although in
are determined in general by cosets and their bijections, although ina slightly less direct manner than the
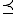 -comparable case. In particular, given two incomparable D-classes A and B with join D-class J and meet D-class
-comparable case. In particular, given two incomparable D-classes A and B with join D-class J and meet D-class 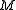 in
in  , interesting connections arise between the two coset decompositions of J (or M) with respect to A and B. (See Section 3.)
, interesting connections arise between the two coset decompositions of J (or M) with respect to A and B. (See Section 3.)Thus a skew lattice may be viewed as a coset atlas of rectangular skew lattices placed on the vertices of a lattice and coset bijections between them, the latter seen as partial isomorphisms
between the rectangular algebras with each coset bijection determining a corresponding pair of cosets. This perspective gives, in essence, the Hasse diagram of the skew lattice, which is easily
drawn in cases of relatively small order. (See the diagrams in Section 3 above.) Given a chain of D-classes
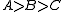 in
in 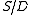 , one has three sets of coset bijections: from A to B, from B to C and from A to C. In general, given coset bijections
, one has three sets of coset bijections: from A to B, from B to C and from A to C. In general, given coset bijections  and
and 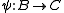 , the composition of partial bijections
, the composition of partial bijections 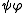 could be empty. If it is not, then a unique coset bijection
could be empty. If it is not, then a unique coset bijection 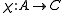 exists such that
exists such that 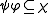 . (Again,
. (Again,  is a bijection between a pair of cosets in
is a bijection between a pair of cosets in  and
and 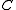 .) This inclusion can be strict. It is always an equality (given
.) This inclusion can be strict. It is always an equality (given 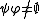 ) on a given skew lattice S precisely when S is categorical. In this case, by including the identity maps on each rectangular D-class and adjoining empty bijections between properly comparable D-classes, one has a category of rectangular algebras and coset bijections between them. The simple examples in Section 3 are categorical.
) on a given skew lattice S precisely when S is categorical. In this case, by including the identity maps on each rectangular D-class and adjoining empty bijections between properly comparable D-classes, one has a category of rectangular algebras and coset bijections between them. The simple examples in Section 3 are categorical.

