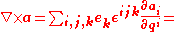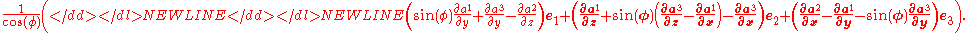Skew coordinates
Encyclopedia
A system of skew coordinates is a coordinate system
where the coordinate surfaces are not orthogonal, in contrast to orthogonal coordinates
.
Skew coordinates tend to be more complicated to work with compared to orthogonal coordinates since the metric tensor
will have nonzero off-diagonal components, preventing many drastic simplifications in formulas for tensor algebra
and tensor calculus. The nonzero off-diagonal components of the metric tensor are a direct result of the non-orthogonality of the basis vectors of the coordinates, since by definition:

where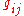 is the metric tensor and
is the metric tensor and  the (covariant) basis vectors.
the (covariant) basis vectors.
These coordinate systems can be useful if the geometry of a problem fits well into a skewed system. For example, solving Laplace's equation
in a parallelogram
will be easiest when done in appropriately skewed coordinates.
 , staying orthogonal to one of the remaining two axes. For this example, the x axis of a Cartesian coordinate has been bent toward the z axis by
, staying orthogonal to one of the remaining two axes. For this example, the x axis of a Cartesian coordinate has been bent toward the z axis by  , remaining orthogonal to the y axis.
, remaining orthogonal to the y axis.
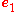 ,
, 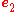 , and
, and 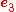 respectively be unit vectors along the
respectively be unit vectors along the  ,
, 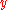 , and
, and  axes. These represent the covariant basis; computing their dot products gives the following components of the metric tensor
axes. These represent the covariant basis; computing their dot products gives the following components of the metric tensor
:
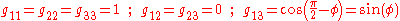
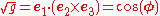
which are quantities that will be useful later on.
The contravariant basis is given by
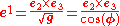
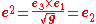
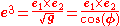
The contravariant basis isn't a very convenient one to use, however it shows up in definitions so must be considered. We'll favor writing quantities with respect to the covariant basis.
Since the basis vectors are all constant, vector addition and subtraction will simply be familiar component-wise adding and subtraction. Now, let

where the sums indicate summation over all values of the index (in this case, i = 1, 2, 3). The contravariant and covariant components of these vectors may be related by
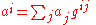
so that, explicitly,
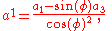

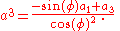
The dot product
in terms of contravariant components is then
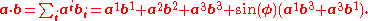
of a scalar function f is
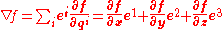
where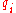 are the coordinates x, y, z indexed. Recognizing this as a vector written in terms of the contravariant basis, it may be rewritten:
are the coordinates x, y, z indexed. Recognizing this as a vector written in terms of the contravariant basis, it may be rewritten:
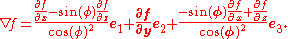
The divergence
of a vector is
is
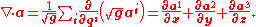
and of a tensor
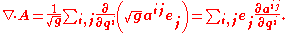
The Laplacian of f is
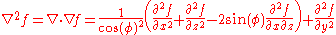
and, since the covariant basis is normal and constant, the vector Laplacian
is the same as the componentwise Laplacian of a vector written in terms of the covariant basis.
While both the dot product and gradient are somewhat messy in that they have extra terms (compared to a Cartesian system) the advection operator
which combines a dot product with a gradient turns out very simple:
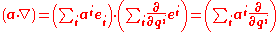
which may be applied to both scalar functions and vector functions, componentwise when expressed in the covariant basis.
Finally, the curl
of a vector is
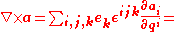
Coordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
where the coordinate surfaces are not orthogonal, in contrast to orthogonal coordinates
Orthogonal coordinates
In mathematics, orthogonal coordinates are defined as a set of d coordinates q = in which the coordinate surfaces all meet at right angles . A coordinate surface for a particular coordinate qk is the curve, surface, or hypersurface on which qk is a constant...
.
Skew coordinates tend to be more complicated to work with compared to orthogonal coordinates since the metric tensor
Metric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
will have nonzero off-diagonal components, preventing many drastic simplifications in formulas for tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
and tensor calculus. The nonzero off-diagonal components of the metric tensor are a direct result of the non-orthogonality of the basis vectors of the coordinates, since by definition:

where
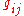 is the metric tensor and
is the metric tensor and  the (covariant) basis vectors.
the (covariant) basis vectors.These coordinate systems can be useful if the geometry of a problem fits well into a skewed system. For example, solving Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
in a parallelogram
Parallelogram
In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
will be easiest when done in appropriately skewed coordinates.
Cartesian coordinates with one skewed axis
The simplest 3D case of a skew coordinate system is a Cartesian one where one of the axes (say the x axis) has been bent by some angle , staying orthogonal to one of the remaining two axes. For this example, the x axis of a Cartesian coordinate has been bent toward the z axis by
, staying orthogonal to one of the remaining two axes. For this example, the x axis of a Cartesian coordinate has been bent toward the z axis by  , remaining orthogonal to the y axis.
, remaining orthogonal to the y axis.Algebra and useful quantities
Let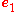 ,
, 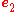 , and
, and 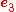 respectively be unit vectors along the
respectively be unit vectors along the  ,
, 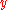 , and
, and  axes. These represent the covariant basis; computing their dot products gives the following components of the metric tensor
axes. These represent the covariant basis; computing their dot products gives the following components of the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
:
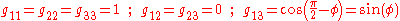
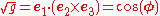
which are quantities that will be useful later on.
The contravariant basis is given by
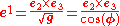
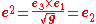
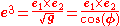
The contravariant basis isn't a very convenient one to use, however it shows up in definitions so must be considered. We'll favor writing quantities with respect to the covariant basis.
Since the basis vectors are all constant, vector addition and subtraction will simply be familiar component-wise adding and subtraction. Now, let

where the sums indicate summation over all values of the index (in this case, i = 1, 2, 3). The contravariant and covariant components of these vectors may be related by
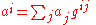
so that, explicitly,
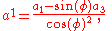

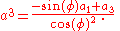
The dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
in terms of contravariant components is then
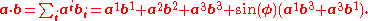
Calculus
By definition, the gradientGradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a scalar function f is
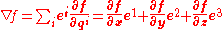
where
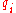 are the coordinates x, y, z indexed. Recognizing this as a vector written in terms of the contravariant basis, it may be rewritten:
are the coordinates x, y, z indexed. Recognizing this as a vector written in terms of the contravariant basis, it may be rewritten: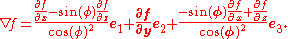
The divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of a vector
 is
is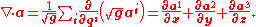
and of a tensor

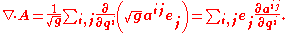
The Laplacian of f is
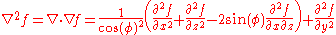
and, since the covariant basis is normal and constant, the vector Laplacian
Vector Laplacian
In mathematics and physics, the vector Laplace operator, denoted by \scriptstyle \nabla^2, named after Pierre-Simon Laplace, is a differential operator defined over a vector field. The vector Laplacian is similar to the scalar Laplacian...
is the same as the componentwise Laplacian of a vector written in terms of the covariant basis.
While both the dot product and gradient are somewhat messy in that they have extra terms (compared to a Cartesian system) the advection operator
Advection
Advection, in chemistry, engineering and earth sciences, is a transport mechanism of a substance, or a conserved property, by a fluid, due to the fluid's bulk motion in a particular direction. An example of advection is the transport of pollutants or silt in a river. The motion of the water carries...
which combines a dot product with a gradient turns out very simple:
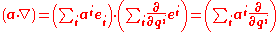
which may be applied to both scalar functions and vector functions, componentwise when expressed in the covariant basis.
Finally, the curl
Curl
In vector calculus, the curl is a vector operator that describes the infinitesimal rotation of a 3-dimensional vector field. At every point in the field, the curl is represented by a vector...
of a vector is