
Singular Spectrum Analysis
Encyclopedia
Singular spectrum analysis (SSA) combines elements of classical time series
analysis, multivariate statistics
, multivariate geometry, dynamical systems and signal processing
. Its roots lie in the classical Karhunen (1946)–Loève (1945, 1978) spectral decomposition of time series
and random fields and in the Mañé (1981)–Takens (1981) embedding theorem
.
In practice, SSA is a nonparametric spectral estimation method based on embedding a time series
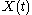 :
:  in a vector space of dimension
in a vector space of dimension  . SSA proceeds by diagonalizing the
. SSA proceeds by diagonalizing the 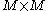 lag-covariance matrix
lag-covariance matrix  of
of 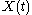 to obtain spectral information on the time series, assumed to be stationary
to obtain spectral information on the time series, assumed to be stationary
in the weak sense. The matrix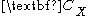 can be estimated directly from the data as a Toeplitz matrix with constant diagonals (Vautard and Ghil, 1989), i.e., its entries
can be estimated directly from the data as a Toeplitz matrix with constant diagonals (Vautard and Ghil, 1989), i.e., its entries 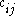 depend only on the lag
depend only on the lag  :
:
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
analysis, multivariate statistics
Multivariate statistics
Multivariate statistics is a form of statistics encompassing the simultaneous observation and analysis of more than one statistical variable. The application of multivariate statistics is multivariate analysis...
, multivariate geometry, dynamical systems and signal processing
Signal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
. Its roots lie in the classical Karhunen (1946)–Loève (1945, 1978) spectral decomposition of time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
and random fields and in the Mañé (1981)–Takens (1981) embedding theorem
Takens' theorem
In mathematics, a delay embedding theorem gives the conditions under which a chaotic dynamical system can be reconstructed from a sequence of observations of the state of a dynamical system...
.
In practice, SSA is a nonparametric spectral estimation method based on embedding a time series
Time series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
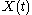 :
:  in a vector space of dimension
in a vector space of dimension  . SSA proceeds by diagonalizing the
. SSA proceeds by diagonalizing the 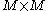 lag-covariance matrix
lag-covariance matrix  of
of 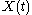 to obtain spectral information on the time series, assumed to be stationary
to obtain spectral information on the time series, assumed to be stationaryStationary process
In the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
in the weak sense. The matrix
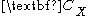 can be estimated directly from the data as a Toeplitz matrix with constant diagonals (Vautard and Ghil, 1989), i.e., its entries
can be estimated directly from the data as a Toeplitz matrix with constant diagonals (Vautard and Ghil, 1989), i.e., its entries 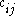 depend only on the lag
depend only on the lag  :
:-
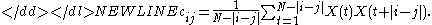
An alternative way to compute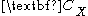 , is by using the
, is by using the  ``trajectory matrix"
``trajectory matrix" 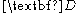 that is formed by
that is formed by  lag-shifted copies of
lag-shifted copies of 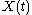 , which are
, which are 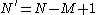 long; then
long; then

The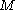 eigenvectors
eigenvectors  of the lag-covariance matrix
of the lag-covariance matrix  are called temporal empirical orthogonal functions (EOFs)Empirical orthogonal functionsIn statistics and signal processing, the method of empirical orthogonal function analysis is a decomposition of a signal or data set in terms of orthogonal basis functions which are determined from the data. It is the same as performing a principal components analysis on the data, except that the...
are called temporal empirical orthogonal functions (EOFs)Empirical orthogonal functionsIn statistics and signal processing, the method of empirical orthogonal function analysis is a decomposition of a signal or data set in terms of orthogonal basis functions which are determined from the data. It is the same as performing a principal components analysis on the data, except that the...
. The eigenvalues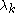 of
of  account for the partial variance in the
account for the partial variance in the
direction and the sum of the eigenvalues, i.e., the trace of
and the sum of the eigenvalues, i.e., the trace of
 , gives the total variance of the original time series
, gives the total variance of the original time series
 . The name of the method derives from the singular values
. The name of the method derives from the singular values  of
of 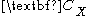 .
.
Decomposition and reconstruction
Projecting the time series onto each EOF yields the corresponding
temporal principal components (PCs)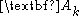 :
:
-

An oscillatory mode is characterized by a pair of
nearly equal SSA eigenvalues and associated PCs that are in approximate phase quadrature (Ghil et al., 2002). Such a pair can represent efficiently a nonlinear, anharmonic oscillation. This is due to the fact that a single pair of data-adaptive SSA eigenmodes often will capture better the basic periodicity of an oscillatory mode than methods with fixed basis functions, such as the and
and 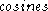 used in the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
used in the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
.
The window width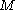 determines the longest periodicity captured by
determines the longest periodicity captured by
SSA. Signal-to-noise separation can be obtained by merely inspecting the slope break in a "scree diagram" of eigenvalues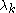 or singular values
or singular values  vs.
vs. 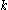 . The point
. The point 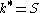 at which this break occurs should not be confused with a ``dimension"
at which this break occurs should not be confused with a ``dimension" 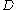 of the underlying deterministic dynamics (Vautard and Ghil, 1989).
of the underlying deterministic dynamics (Vautard and Ghil, 1989).
A Monte-Carlo test (Allen and Robertson, 1996) can be applied to ascertain the statistical significance of the oscillatory pairs detected by SSA. The entire time series or parts of it that correspond to trends, oscillatory modes or noise can be reconstructed by using linear combinations of the PCs and EOFs, which provide the reconstructed components (RCs)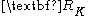 :
:
-
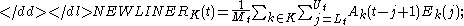
here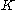 is the set of EOFs on which the reconstruction is based. The values of the normalization factor
is the set of EOFs on which the reconstruction is based. The values of the normalization factor 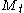 , as well as of the lower and upper bound of summation
, as well as of the lower and upper bound of summation 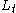 and
and 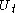 , differ between the central part of the time series and the vicinity of its endpoints (Ghil et al., 2002).
, differ between the central part of the time series and the vicinity of its endpoints (Ghil et al., 2002).
Multivariate extension
Multi-channel SSA (or M-SSA) is a natural extension of SSA to an -channel time series of vectors or maps with
-channel time series of vectors or maps with 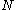 data points
data points  . In the meteorological literature, extended EOF (EEOF) analysis is often assumed to be synonymous with M-SSA. The two methods are both extensions of classical principal component analysis (PCA)Principal components analysisPrincipal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
. In the meteorological literature, extended EOF (EEOF) analysis is often assumed to be synonymous with M-SSA. The two methods are both extensions of classical principal component analysis (PCA)Principal components analysisPrincipal component analysis is a mathematical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of uncorrelated variables called principal components. The number of principal components is less than or equal to...
but they differ in emphasis: EEOF analysis typically utilizes a number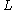 of spatial channels much greater than the number
of spatial channels much greater than the number 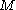 of temporal lags, thus limiting the temporal and spectral information. In M-SSA, on the other hand, one usually chooses
of temporal lags, thus limiting the temporal and spectral information. In M-SSA, on the other hand, one usually chooses  . Often M-SSA is applied to a few leading PCs of the spatial data, with
. Often M-SSA is applied to a few leading PCs of the spatial data, with 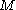 chosen large enough to extract detailed temporal and spectral information from the multivariate time series (Ghil et al., 2002).
chosen large enough to extract detailed temporal and spectral information from the multivariate time series (Ghil et al., 2002).
Spatio-temporal gap filling
The gap-filling version of SSA can be used to analyze data sets that are unevenly sampled or contain missing data (Kondrashov and Ghil, 2006). For a univariate time series, the SSA gap filling procedure utilizes temporal correlations to fill in the missing points. For a multivariate data set, gap filling by M-SSA takes advantage of both spatial and temporal correlations. In either case: (i) estimates of missing data points are produced iteratively, and are then used to compute a self-consistent lag-covariance matrix and its EOFs
and its EOFs 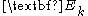 ; and (ii) cross-validation is used to optimize the window width
; and (ii) cross-validation is used to optimize the window width  and the number of leading SSA modes to fill the gaps with the iteratively estimated "signal," while the noise is discarded.
and the number of leading SSA modes to fill the gaps with the iteratively estimated "signal," while the noise is discarded.
Brief history
Broomhead and King (1986a, b) proposed to use SSA and M-SSA in the context of nonlinear dynamics for the purpose of reconstructing the attractorAttractorAn attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
of a system from measured time series. These authors provided an extension and a more robust application of the Mañé (1981)-Takens (1981) idea of reconstructing dynamics from a single time series.
Ghil, Vautard and associates (Vautard and Ghil, 1989; Ghil and Vautard, 1991; Vautard et al., 1992) noticed the analogy between the trajectory matrix of Broomhead and King, on the one hand, and Karhunen (1946)-Loève (1945) principal component analysis in the time domain, on the other. Thus, SSA can be used as a time-and-frequency domain method for time seriesTime seriesIn statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
analysis — independently from attractorAttractorAn attractor is a set towards which a dynamical system evolves over time. That is, points that get close enough to the attractor remain close even if slightly disturbed...
reconstruction and including cases in which the latter may fail.
At present, the papers dealing with the methodological aspects and the applications of SSA number in the hundreds. Introductions to and reviews of the literature are provided by Elsner and Tsonis (1996), Danilov and Zhigljavsky (1997), Golyandina et al. (2001), and Ghil et al. (2002).
See also
- Multitaper methodMultitaperIn signal processing, the multitaper method is a technique developed by David J. Thomson to estimate the power spectrum SX of a stationary ergodic finite-variance random process X, given a finite contiguous realization of X as data....
- Short-time Fourier transformShort-time Fourier transformThe short-time Fourier transform , or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time....
- Spectral density estimationSpectral density estimationIn statistical signal processing, the goal of spectral density estimation is to estimate the spectral density of a random signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal...
External links
- Multitaper method
-
-

