Simplex noise
Encyclopedia
Simplex noise is a method for constructing an n-dimensional noise function comparable to Perlin noise
("classic" noise) but with a lower computational overhead, especially in larger dimensions. Ken Perlin
designed the algorithm in 2001 to address the limitations of his classic noise function, especially in higher dimensions.
The advantages of simplex noise over Perlin noise:
Whereas classical noise interpolates between the values from the surrounding hypergrid end points (ie: North South East West in 2D), Simplex noise divides the space into simplex
es (i.e. N-dimensional equilateral triangles) to interpolate between. This reduces the number of data points. While a hypercube in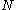
dimensions has 
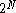corners, a simplex in 
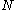dimensions has only 
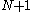corners.
Perlin noise
Perlin noise is a computer-generated visual effect developed by Ken Perlin, who won an Academy Award for its use in the motion picture Tron...
("classic" noise) but with a lower computational overhead, especially in larger dimensions. Ken Perlin
Ken Perlin
Ken Perlin is a professor in the Department of Computer Science at New York University, founding director of the Media Research Lab at NYU, and the Director of the Games for Learning Institute. His research interests include graphics, animation, multimedia, and science education...
designed the algorithm in 2001 to address the limitations of his classic noise function, especially in higher dimensions.
The advantages of simplex noise over Perlin noise:
- Simplex noise has a lower computational complexity and requires fewer multiplications.
- Simplex noise scales to higher dimensions (4D, 5D and up) with much less computational cost, the complexity is
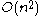for 
dimensions instead of the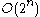 
of classic Noise. - Simplex noise has no noticeable directional artifacts (is isotropic).
- Simplex noise has a well-defined and continuous gradient everywhere that can be computed quite cheaply.
- Simplex noise is easy to implement in hardware.
Whereas classical noise interpolates between the values from the surrounding hypergrid end points (ie: North South East West in 2D), Simplex noise divides the space into simplex
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
es (i.e. N-dimensional equilateral triangles) to interpolate between. This reduces the number of data points. While a hypercube in
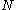dimensions has 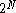corners, a simplex in 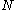dimensions has only 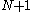corners.