Silhouette (clustering)
Encyclopedia
Silhouette refers to a method of interpretation and validation of clusters of data. The technique provides a succinct graphical representation of how well each object lies within its cluster. It was first described by Peter J. Rousseeuw in 1986.
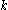clusters. For each datum
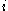, let 
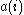be the average dissimilarity of 
with all other data within the same cluster. Any measure of dissimilarity can be used but distance measures
are the most common. We can interpret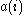
as how well matched 
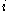is to the cluster it is assigned (the smaller the value, the better the matching). Then find the average dissimilarity of 
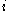with the data of another single cluster. Repeat this for every cluster of which 
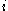is not a member. Denote the lowest average dissimilarity to 
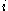of any such cluster by 
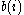. The cluster with this average dissimilarity is said to be the "neighbouring cluster" of 
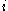as it is, aside from the cluster 
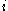is assigned, the cluster in which 
fits best.
We now define:
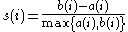
Which can be written as: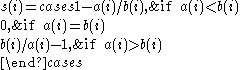
From the above definition it is clear that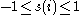
For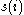
to be close to 1 we require 
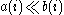. As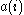 
is a measure of how dissimilar 
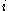is to its own cluster, a small value means it is well matched. Furthermore, a large 
implies that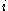 
is badly matched to its neighbouring cluster. Thus an 
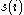close to one means that the datum is appropriately clustered.
If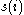
is close to negative one, then by the same logic we see that 
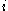would be more appropriate if it was clustered in its neighbouring cluster. An 
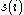near zero means that the datum is on the border of two natural clusters.
The average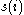
of a cluster is a measure of how tightly grouped all the data in the cluster are. Thus the average 
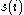of the entire dataset is a measure of how appropriately the data has been clustered. If there are too many or too few clusters, as may occur when a poor choice of 
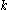is used in the k-means algorithm, some of the clusters will typically display much narrower silhouettes than the rest. Thus silhouette plots and averages may be used to determine the natural number of clusters within a dataset.
Method
Assume the data have been clustered via any technique, such as k-means, into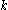 clusters. For each datumData
The term data refers to qualitative or quantitative attributes of a variable or set of variables. Data are typically the results of measurements and can be the basis of graphs, images, or observations of a set of variables. Data are often viewed as the lowest level of abstraction from which...
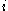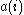, let be the average dissimilarity of with all other data within the same cluster. Any measure of dissimilarity can be used but distance measuresDistance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
are the most common. We can interpret
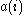as how well matched 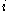is to the cluster it is assigned (the smaller the value, the better the matching). Then find the average dissimilarity of 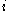with the data of another single cluster. Repeat this for every cluster of which 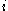is not a member. Denote the lowest average dissimilarity to 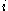of any such cluster by 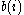. The cluster with this average dissimilarity is said to be the "neighbouring cluster" of 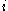as it is, aside from the cluster 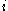is assigned, the cluster in which fits best.We now define:
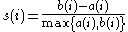
Which can be written as:
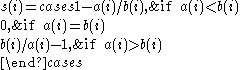
From the above definition it is clear that
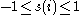
For
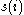to be close to 1 we require 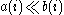. As 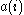is a measure of how dissimilar 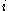is to its own cluster, a small value means it is well matched. Furthermore, a large implies that 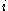is badly matched to its neighbouring cluster. Thus an 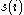close to one means that the datum is appropriately clustered.If
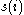is close to negative one, then by the same logic we see that 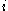would be more appropriate if it was clustered in its neighbouring cluster. An 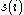near zero means that the datum is on the border of two natural clusters.The average
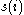of a cluster is a measure of how tightly grouped all the data in the cluster are. Thus the average 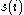of the entire dataset is a measure of how appropriately the data has been clustered. If there are too many or too few clusters, as may occur when a poor choice of 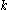is used in the k-means algorithm, some of the clusters will typically display much narrower silhouettes than the rest. Thus silhouette plots and averages may be used to determine the natural number of clusters within a dataset.