
Self-averaging
Encyclopedia
A self-averaging physical property of a disordered system is one that can be described by averaging over a sufficiently large sample. The concept was introduced by Ilya Mikhailovich Lifshitz.
one comes across situations where quenched randomness plays an important role. Any physical property
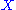 of such a system, would require an averaging over all disorder realisations. The system can be completely described by the average
of such a system, would require an averaging over all disorder realisations. The system can be completely described by the average 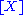 where
where  denotes an averaging over realisations (“averaging over samples”) provided the relative variance RX = VX/[X]2 → 0 for large
denotes an averaging over realisations (“averaging over samples”) provided the relative variance RX = VX/[X]2 → 0 for large  , where VX = [X2] − [X]2. In such a scenario a single large system is sufficient to represent the whole ensemble. Such quantities are called self-averaging. Away from criticality, when the larger lattice is built from smaller blocks, then due to the additivity property of an extensive quantity, the central limit theorem
, where VX = [X2] − [X]2. In such a scenario a single large system is sufficient to represent the whole ensemble. Such quantities are called self-averaging. Away from criticality, when the larger lattice is built from smaller blocks, then due to the additivity property of an extensive quantity, the central limit theorem
guarantees that RX → N−1 thereby ensuring self-averaging. On the other hand, at the critical point, the question whether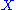 is self-averaging or not becomes nontrivial, due to long range correlation
is self-averaging or not becomes nontrivial, due to long range correlation
s.
decay RX ~ N−z with 0 < z < 1. Such systems are classified weakly self-averaging. The known critical exponents of the system determine the exponent z.
It must also be added that relevant randomness does not necessarily imply non self-averaging, especially in a mean-field scenario
. The RG arguments mentioned above need to be extended to situations with sharp limit of Tc distribution and long range interactions.
Definition
Frequently in physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
one comes across situations where quenched randomness plays an important role. Any physical property
Physical property
A physical property is any property that is measurable whose value describes a physical system's state. The changes in the physical properties of a system can be used to describe its transformations ....
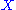 of such a system, would require an averaging over all disorder realisations. The system can be completely described by the average
of such a system, would require an averaging over all disorder realisations. The system can be completely described by the average 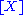 where
where  denotes an averaging over realisations (“averaging over samples”) provided the relative variance RX = VX/[X]2 → 0 for large
denotes an averaging over realisations (“averaging over samples”) provided the relative variance RX = VX/[X]2 → 0 for large  , where VX = [X2] − [X]2. In such a scenario a single large system is sufficient to represent the whole ensemble. Such quantities are called self-averaging. Away from criticality, when the larger lattice is built from smaller blocks, then due to the additivity property of an extensive quantity, the central limit theorem
, where VX = [X2] − [X]2. In such a scenario a single large system is sufficient to represent the whole ensemble. Such quantities are called self-averaging. Away from criticality, when the larger lattice is built from smaller blocks, then due to the additivity property of an extensive quantity, the central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
guarantees that RX → N−1 thereby ensuring self-averaging. On the other hand, at the critical point, the question whether
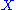 is self-averaging or not becomes nontrivial, due to long range correlation
is self-averaging or not becomes nontrivial, due to long range correlationCorrelation
In statistics, dependence refers to any statistical relationship between two random variables or two sets of data. Correlation refers to any of a broad class of statistical relationships involving dependence....
s.
Non self-averaging systems
At the pure critical point randomness is classified as relevant if, by the standard definition of relevance, it leads to a change in the critical behaviour (i.e., the critical exponents) of the pure system. It has been shown by recent renormalization group and numerical studies that self-averaging property is lost if randomness or disorder is relevant. Most importantly as N → ∞, RX at the critical point approaches a constant. Such systems are called non self-averaging. Thus unlike the self-averaging scenario, numerical simulations cannot lead to an improved picture in larger lattices (large N), even if the critical point is exactly known. In summary, various types of self-averaging can be indexed with the help of the asymptotic size dependence of a quantity like RX. If RX falls off to zero with size, it is self-averaging whereas if RX approaches a constant as N → ∞, the system is non-self-averaging.Strong and weak self-averaging
There is a further classification of Self-averaging systems as strong and weak. If the exhibited behavior is RX ~ N−1 as suggested by the central limit theorem, mentioned earlier, the system is said to be strongly self-averaging. Some systems shows a slower power lawPower law
A power law is a special kind of mathematical relationship between two quantities. When the frequency of an event varies as a power of some attribute of that event , the frequency is said to follow a power law. For instance, the number of cities having a certain population size is found to vary...
decay RX ~ N−z with 0 < z < 1. Such systems are classified weakly self-averaging. The known critical exponents of the system determine the exponent z.
It must also be added that relevant randomness does not necessarily imply non self-averaging, especially in a mean-field scenario
. The RG arguments mentioned above need to be extended to situations with sharp limit of Tc distribution and long range interactions.

