
Seismic tomography
Encyclopedia
Seismic tomography is a methodology for estimating the Earth's properties. In the seismology
community, seismic tomography
is just a part of seismic imaging, and usually has a more specific purpose to estimate properties such as propagating velocities of compressional waves (P-wave
) and shear waves (S-wave
). It can also be used to recover the attenuation
factor Q. Another branch of seismic imaging is seismic migration in which the properties to be estimated include the reflection coefficient or reflectivity.
In another way, we define tomography as a technique whereby a 3-dimensional images are derived from the processing of integrated properties of the medium that rays encounter along their paths through it. Seismic tomography refers to the derivation of the 3-dimensional velocity structure of earth from seismic waves.
The simplest case of seismic tomography is to estimate P-wave velocity. Several methods have been developed for this purpose, e.g., refraction traveltime tomography, finite-frequency traveltime tomography, reflection traveltime tomography, waveform tomography.
Seismic tomography is usually formulated as an inverse problem
. In refraction traveltime tomography, the observed data are the first-arrival traveltimes and the model parameters are the slowness
and the model parameters are the slowness  . The forward problem can be formulated as
. The forward problem can be formulated as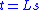
where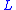 is the forward operator which, in this case, is the raypath matrix.
is the forward operator which, in this case, is the raypath matrix.
Refraction traveltime tomography is computationally efficient but can only provide a low-resolution image of the subsurface.
To obtain a higher-resolution image one has to abandon the infinite-frequency approximations of ray theory that are applicable to the time of the
wave 'onset' and instead measure travel times (or amplitudes) over a time window of some length using cross-correlation.
Finite-frequency tomography takes the effects of wave diffraction into
account, which makes the imaging of smaller objects or anomalies possible. The raypaths are replaced by volumetric sensitivity kernels, often named 'banana-doughnut'
kernels in global tomography, because their shape may resemble a banana, whereas their cross-section looks like a doughnut, with, at least for direct P and S waves,
zero sensitivity of the travel time on the geometrical ray path. In finite-frequency tomography, travel time and amplitude anomalies are frequency-dependent, which leads to an increase in resolution.
To exploit the information in a seismogram to the fullest, one uses waveform tomography. In this case, the seismograms are the observed data. In seismic exploration, the forward model is usually governed by the acoustic wave equation. This is an approximation to the elastic wave propagation. Elastic waveform tomography is much more difficult than acoustic waveform tomography. The acoustic wave equation is numerically solved by some numerical schemes such as finite-difference and finite-element methods. Seismic waveform tomography can be efficiently solved by adjoint methods.
Seismology
Seismology is the scientific study of earthquakes and the propagation of elastic waves through the Earth or through other planet-like bodies. The field also includes studies of earthquake effects, such as tsunamis as well as diverse seismic sources such as volcanic, tectonic, oceanic,...
community, seismic tomography
Tomography
Tomography refers to imaging by sections or sectioning, through the use of any kind of penetrating wave. A device used in tomography is called a tomograph, while the image produced is a tomogram. The method is used in radiology, archaeology, biology, geophysics, oceanography, materials science,...
is just a part of seismic imaging, and usually has a more specific purpose to estimate properties such as propagating velocities of compressional waves (P-wave
P-wave
P-waves are a type of elastic wave, also called seismic waves, that can travel through gases , solids and liquids, including the Earth. P-waves are produced by earthquakes and recorded by seismographs...
) and shear waves (S-wave
S-wave
A type of seismic wave, the S-wave, secondary wave, or shear wave is one of the two main types of elastic body waves, so named because they move through the body of an object, unlike surface waves....
). It can also be used to recover the attenuation
Attenuation
In physics, attenuation is the gradual loss in intensity of any kind of flux through a medium. For instance, sunlight is attenuated by dark glasses, X-rays are attenuated by lead, and light and sound are attenuated by water.In electrical engineering and telecommunications, attenuation affects the...
factor Q. Another branch of seismic imaging is seismic migration in which the properties to be estimated include the reflection coefficient or reflectivity.
In another way, we define tomography as a technique whereby a 3-dimensional images are derived from the processing of integrated properties of the medium that rays encounter along their paths through it. Seismic tomography refers to the derivation of the 3-dimensional velocity structure of earth from seismic waves.
The simplest case of seismic tomography is to estimate P-wave velocity. Several methods have been developed for this purpose, e.g., refraction traveltime tomography, finite-frequency traveltime tomography, reflection traveltime tomography, waveform tomography.
Seismic tomography is usually formulated as an inverse problem
Inverse problem
An inverse problem is a general framework that is used to convert observed measurements into information about a physical object or system that we are interested in...
. In refraction traveltime tomography, the observed data are the first-arrival traveltimes
 and the model parameters are the slowness
and the model parameters are the slowness  . The forward problem can be formulated as
. The forward problem can be formulated as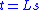
where
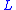 is the forward operator which, in this case, is the raypath matrix.
is the forward operator which, in this case, is the raypath matrix.Refraction traveltime tomography is computationally efficient but can only provide a low-resolution image of the subsurface.
To obtain a higher-resolution image one has to abandon the infinite-frequency approximations of ray theory that are applicable to the time of the
wave 'onset' and instead measure travel times (or amplitudes) over a time window of some length using cross-correlation.
Finite-frequency tomography takes the effects of wave diffraction into
account, which makes the imaging of smaller objects or anomalies possible. The raypaths are replaced by volumetric sensitivity kernels, often named 'banana-doughnut'
kernels in global tomography, because their shape may resemble a banana, whereas their cross-section looks like a doughnut, with, at least for direct P and S waves,
zero sensitivity of the travel time on the geometrical ray path. In finite-frequency tomography, travel time and amplitude anomalies are frequency-dependent, which leads to an increase in resolution.
To exploit the information in a seismogram to the fullest, one uses waveform tomography. In this case, the seismograms are the observed data. In seismic exploration, the forward model is usually governed by the acoustic wave equation. This is an approximation to the elastic wave propagation. Elastic waveform tomography is much more difficult than acoustic waveform tomography. The acoustic wave equation is numerically solved by some numerical schemes such as finite-difference and finite-element methods. Seismic waveform tomography can be efficiently solved by adjoint methods.

