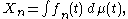Second moment method
Encyclopedia
In mathematics, the second moment method is a technique used in probability theory
and analysis
to show that a random variable
has positive probability of being positive. More generally, the "moment method" consists of bounding the probability that a random variable fluctuates far from its mean, by using its moments.
The method is often quantitative, in that one can often deduce a lower bound on the probability that the random variable is larger than some constant times its expectation. The method involves comparing the second moment
of random variables to the square of the first moment.
for integer-valued variables. For a non-negative, integer-valued random variable
, we may want to prove that 
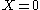with high probability. To obtain an upper bound for 
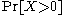, and thus a lower bound for 
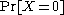, we first note that since 
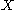takes only integer values, 
. Since 
is non-negative we can now apply Markov's inequality
to obtain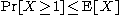
. Combining these we have 
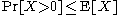; the first moment method is simply the use of this inequality.
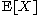being "large" does not directly imply that 
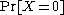is small. However, we can often use the second moment to derive such a conclusion, using some form of Chebyshev's inequality
.
Suppose that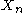
is a sequence of non-negative real-valued random variables which converge in law to a random variable 
. If there are finite positive constants 
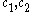such that
and
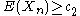
hold for every
, then it follows from the Paley–Zygmund inequality
that for every
and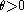 
Consequently, the same inequality is satisfied by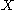
. In many situations, instead of using the Paley–Zygmund inequality, it is sufficient to use Cauchy–Schwarz
.
T is an infinite tree
where one vertex (called the root) has two neighbors and every other vertex has three neighbors. The second moment method can be used to show that at every parameter p ∈( 1/2, 1] with positive probability the connected component of the root in the percolation subgraph of T is infinite.
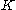be the percolation component of the root, and let 
be the set of vertices of 
that are at distance 
from the root. Let 
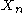be the number of vertices in 
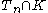. To prove that 
is infinite with positive probability, it is enough to show that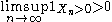 
with positive probability. By the reverse Fatou lemma, it suffices to show that 
.
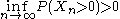The Cauchy–Schwarz inequality
gives
Therefore, it is sufficient to show that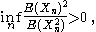
that is, that the second moment is bounded from above by a constant times the first moment squared (and both are nonzero). In many applications of the second moment method, one is not able to calculate the moments precisely, but can nevertheless establish this inequality.
In this particular application, these moments can be calculated. For every specific
,
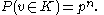
Since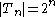
, it follows that
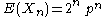
which is the first moment.
Now comes the second moment calculation.
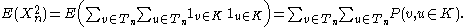
For each pair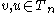
let 
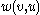denote the vertex in 
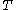that is farthest away from the root and lies on the simple path in 
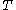to each of the two vertices 
and 
, and let 
denote the distance from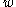 
to the root. In order for 
to both be in 
, it is necessary and sufficient for the three simple paths from 
to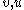 
and the root to be in 
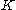. Since the number of edges contained in the union of these three paths is 
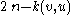, we obtain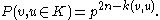
The number of pairs
such that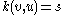 
is equal to 
, for 
. Hence,
which completes the proof.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and analysis
Analysis
Analysis is the process of breaking a complex topic or substance into smaller parts to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle , though analysis as a formal concept is a relatively recent development.The word is...
to show that a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
has positive probability of being positive. More generally, the "moment method" consists of bounding the probability that a random variable fluctuates far from its mean, by using its moments.
The method is often quantitative, in that one can often deduce a lower bound on the probability that the random variable is larger than some constant times its expectation. The method involves comparing the second moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of random variables to the square of the first moment.
First moment method
The first moment method is a simple application of Markov's inequalityMarkov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
for integer-valued variables. For a non-negative, integer-valued random variable
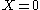, we may want to prove that with high probability. To obtain an upper bound for 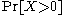, and thus a lower bound for 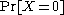, we first note that since 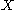takes only integer values, . Since is non-negative we can now apply Markov's inequalityMarkov's inequality
In probability theory, Markov's inequality gives an upper bound for the probability that a non-negative function of a random variable is greater than or equal to some positive constant...
to obtain
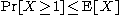. Combining these we have 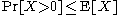; the first moment method is simply the use of this inequality.General outline of the second moment method
In the other direction,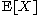 being "large" does not directly imply that 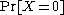is small. However, we can often use the second moment to derive such a conclusion, using some form of Chebyshev's inequalityChebyshev's inequality
In probability theory, Chebyshev’s inequality guarantees that in any data sample or probability distribution,"nearly all" values are close to the mean — the precise statement being that no more than 1/k2 of the distribution’s values can be more than k standard deviations away from the mean...
.
Suppose that
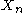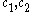is a sequence of non-negative real-valued random variables which converge in law to a random variable . If there are finite positive constants such thatand
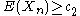
hold for every
, then it follows from the Paley–Zygmund inequalityPaley–Zygmund inequality
In mathematics, the Paley–Zygmund inequality bounds theprobability that a positive random variable is small, in terms ofits mean and variance...
that for every
and 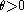Consequently, the same inequality is satisfied by
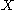. In many situations, instead of using the Paley–Zygmund inequality, it is sufficient to use Cauchy–SchwarzCauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
.
Setup of problem
The Bernoulli bond percolation subgraph of a graph G at parameter p is a random subgraph obtained from G by deleting every edge of G with probability 1 − p, independently. The infinite complete binary treeBinary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
T is an infinite tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
where one vertex (called the root) has two neighbors and every other vertex has three neighbors. The second moment method can be used to show that at every parameter p ∈
Application of method
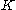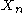Let be the percolation component of the root, and let be the set of vertices of that are at distance from the root. Let be the number of vertices in 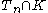. To prove that is infinite with positive probability, it is enough to show that 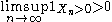with positive probability. By the reverse Fatou lemma, it suffices to show that 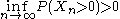.The Cauchy–Schwarz inequality
Cauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
gives
Therefore, it is sufficient to show that
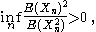
that is, that the second moment is bounded from above by a constant times the first moment squared (and both are nonzero). In many applications of the second moment method, one is not able to calculate the moments precisely, but can nevertheless establish this inequality.
In this particular application, these moments can be calculated. For every specific
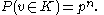
,Since
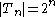, it follows that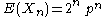which is the first moment.
Now comes the second moment calculation.
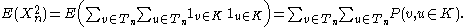
For each pair
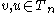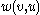let denote the vertex in 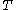that is farthest away from the root and lies on the simple path in 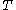to each of the two vertices and , and let denote the distance from 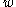to the root. In order for to both be in , it is necessary and sufficient for the three simple paths from to 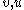and the root to be in 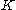. Since the number of edges contained in the union of these three paths is 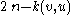, we obtain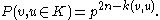The number of pairs
such that 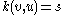is equal to , for . Hence,which completes the proof.
Discussion
- The choice of the random variables Xn was rather natural in this setup. In some more difficult applications of the method, some ingenuity might be required in order to choose the random variables Xn for which the argument can be carried through.
- The Paley–Zygmund inequalityPaley–Zygmund inequalityIn mathematics, the Paley–Zygmund inequality bounds theprobability that a positive random variable is small, in terms ofits mean and variance...
is sometimes used instead of Cauchy–Schwarz and may occasionally give more refined results. - Under the (incorrect) assumption that the events
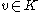and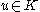 
are always independent, one has 
, and the second moment is equal to the first moment squared. The second moment method typically works in situations in which the corresponding events or random variables are “nearly independent". - In this application, the random variables Xn are given as sums
-
-
- In other applications, the corresponding useful random variables are integralIntegralIntegration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
s -
- where the functions ƒn are random. In such a situation, one considers the product measure μ × μ and calculates
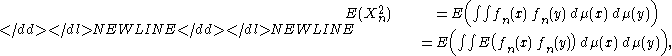
- where the last step is typically justified using Fubini's theoremFubini's theoremIn mathematical analysis Fubini's theorem, named after Guido Fubini, is a result which gives conditions under which it is possible to compute a double integral using iterated integrals. As a consequence it allows the order of integration to be changed in iterated integrals.-Theorem...
.
- where the last step is typically justified using Fubini's theorem
