Scoring rule
Encyclopedia
In decision theory
a score function, or scoring rule, is a measure of the performance of an entity, be it person or machine, that repeatedly makes decisions under uncertainty. For example, every evening a TV weather forecaster
may give the probability of rain on the next day, in a type of probabilistic forecasting
. A viewer could note the number of times that a 25% probability was quoted, over a ten year period, and compare this with the actual proportion of times that rain fell. If the actual percentage was substantially different from the stated probability we say that the forecaster is poorly calibrated
. A poorly calibrated forecaster might be encouraged to do better by a bonus
system. A bonus system designed around a proper scoring rule will incentivize the forecaster to report probabilities equal to his personal beliefs.
decision, such as assigning probabilities to 'rain' or 'no rain', scoring rules may take on a simpler form. For example, Suppose we reward the forecaster with a reward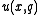
when he makes a rain statement with an attached rain probability 
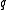and 
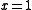if it rains, 
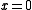if it does not. Assuming that our weatherman wishes to maximise his expected reward he will choose a forecast 
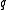which maximises
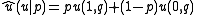
where p is his personal probability that rain will fall.
r with a probability for each of the i outcomes. One usage of a scoring function could be to pay
if the ith event occurs.
All multi-class scoring rules can also be used for binary scoring by setting the number of classes C = 2.
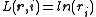
Since strictly proper scoring rules remain strictly proper under linear transformation
is strictly proper for all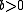 
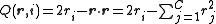
The Brier score
, originally proposed by Glenn W. Brier in 1950, can be obtained by a linear transform from the quadratic scoring rule.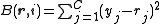
Where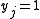
when the jth event is correct and 
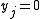otherwise and C is the number of classes.
An important difference between these two rules is that a forecaster should strive to maximize the quadratic score yet minimize the Brier score. This is due to a negative sign in the linear transformation between them.
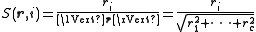
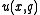is said to be proper if 
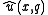is (uniquely) maximized when 
for any value of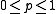 
. The use of a proper scoring rule encourages the forecaster to be honest, as his expected payoff is maximized when he reports his personal rain probability 
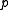as the prediction 
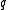. Two commonly used proper score functions are:
The Brier score
,
given by
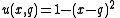
and the logarithmic score function
Decision theory
Decision theory in economics, psychology, philosophy, mathematics, and statistics is concerned with identifying the values, uncertainties and other issues relevant in a given decision, its rationality, and the resulting optimal decision...
a score function, or scoring rule, is a measure of the performance of an entity, be it person or machine, that repeatedly makes decisions under uncertainty. For example, every evening a TV weather forecaster
Weather forecasting
Weather forecasting is the application of science and technology to predict the state of the atmosphere for a given location. Human beings have attempted to predict the weather informally for millennia, and formally since the nineteenth century...
may give the probability of rain on the next day, in a type of probabilistic forecasting
Probabilistic forecasting
Probabilistic forecasting summarises what is known, or opinions about, future events. In contrast to a single-valued forecasts , probabilistic forecasts assign a probability to each of a number of different outcomes,...
. A viewer could note the number of times that a 25% probability was quoted, over a ten year period, and compare this with the actual proportion of times that rain fell. If the actual percentage was substantially different from the stated probability we say that the forecaster is poorly calibrated
Calibrated probability assessment
Calibrated probability assessments are subjective probabilities assigned by individuals who have been trained to assess probabilities in a way that historically represents their uncertainty. In other words, when a calibrated person says they are "80% confident" in each of 100 predictions they...
. A poorly calibrated forecaster might be encouraged to do better by a bonus
Bonus
The word Bonus refers to extra pay due to good performance.Bonus may also refer to:- People :* Lawrence Bonus, a Filipino basketball player* Petrus Bonus, a physician* Bonus , a Byzantine general, active in the reign of Justin II...
system. A bonus system designed around a proper scoring rule will incentivize the forecaster to report probabilities equal to his personal beliefs.
Binary decisions
In the simple case of a binaryBinary
- Mathematics :* Binary numeral system, a representation for numbers using only two digits * Binary function, a function in mathematics that takes two arguments- Computing :* Binary file, composed of something other than human-readable text...
decision, such as assigning probabilities to 'rain' or 'no rain', scoring rules may take on a simpler form. For example, Suppose we reward the forecaster with a reward
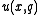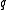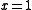when he makes a rain statement with an attached rain probability and if it rains, 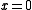if it does not. Assuming that our weatherman wishes to maximise his expected reward he will choose a forecast 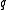which maximises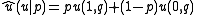where p is his personal probability that rain will fall.
Multi-class scoring rules
Scoring rules can also be used in the case where a forecaster assigns probabilities to multiple classes, such as 'rain', 'snow', or 'clear'. A forecaster will return a Probability vectorProbability vector
Stochastic vector redirects here. For the concept of a random vector, see Multivariate random variable.In mathematics and statistics, a probability vector or stochastic vector is a vector with non-negative entries that add up to one....
r with a probability for each of the i outcomes. One usage of a scoring function could be to pay
if the ith event occurs.All multi-class scoring rules can also be used for binary scoring by setting the number of classes C = 2.
Logarithmic scoring rule
The logarithmic scoring rule is a local strictly proper scoring rule.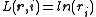Since strictly proper scoring rules remain strictly proper under linear transformation
is strictly proper for all 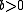Brier/quadratic scoring rule
The quadratic scoring rule is a strictly proper scoring rule.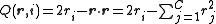The Brier score
Brier score
The Brier score is a proper score function that measures the accuracy of a set of probability assessments. It was proposed by Glenn W. Brier in 1950....
, originally proposed by Glenn W. Brier in 1950, can be obtained by a linear transform from the quadratic scoring rule.
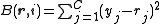
Where
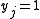when the jth event is correct and 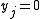otherwise and C is the number of classes.An important difference between these two rules is that a forecaster should strive to maximize the quadratic score yet minimize the Brier score. This is due to a negative sign in the linear transformation between them.
Spherical scoring rule
The spherical scoring rule is also a strictly proper scoring rule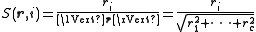Proper scoring rule
A scoring rule is said to be proper if it is optimized for well calibrated probability assessments. A scoring rule is strictly proper if it is uniquely maximized at this point. Optimized in this case will correspond to maximization for the quadratic, spherical, and logarithmic rules but minimization for the Brier Score.Binary proper scoring rule
A scoring rule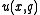 is said to be proper if 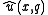is (uniquely) maximized when 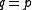for any value of 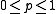. The use of a proper scoring rule encourages the forecaster to be honest, as his expected payoff is maximized when he reports his personal rain probability 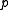as the prediction 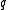. Two commonly used proper score functions are:The Brier score
Brier score
The Brier score is a proper score function that measures the accuracy of a set of probability assessments. It was proposed by Glenn W. Brier in 1950....
,
given by
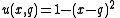
and the logarithmic score function
-
.
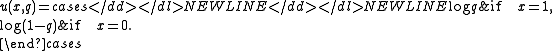Multi-class proper scoring rule
A multi-class scoring rule is said to be proper if it is maximized when r = p. A scoring rule is strictly proper when the score is only maximized when r = p.
Positive-affine transformation
A strictly proper scoring rule, whether binary or multiclass, after a positive-affine transformation remains a strictly proper scoring rule. That is, if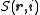
is a strictly proper scoring rule then 
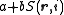with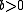 
is also a strictly proper scoring rule.
Locality
A proper scoring rule is said to be local if its value depends only on the probability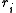
. All binary scores are local because the probability assigned to the event that did not occur is directly producible as 
.
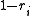The logarithmic scoring rule is an example of a multi-class strictly proper local scoring rule.
External links