
Brier score
Encyclopedia
The Brier score is a proper score function
that measures the accuracy of a set of probability
assessments. It was proposed by Glenn W. Brier in 1950.
It measures the average squared deviation between predicted probabilities for a set of events and their outcomes, so a lower score represents higher accuracy.

In which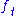 is the probability that was forecast,
is the probability that was forecast, 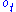 the actual outcome of the event at instance t (0 if it doesn't happen and 1 if it happens) and N is the number of forecasting instances. This formulation is mostly used for binary events (for example "rain" or "no rain").
the actual outcome of the event at instance t (0 if it doesn't happen and 1 if it happens) and N is the number of forecasting instances. This formulation is mostly used for binary events (for example "rain" or "no rain").
Then the Brier score is given by: .
In weather forecasting, a trace (< 0.01) is considered "0.0"

In which R is the number of possible classes in which the event can fall. For the case Rain / No rain, R=2, while for the forecast Cold / Normal / Warm, R=3.
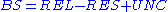
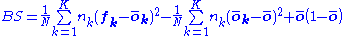
With being the total number of forecasts issued,
being the total number of forecasts issued,  the number of unique forecasts issued,
the number of unique forecasts issued, 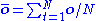 the observed climatological base rate for the event to occur,
the observed climatological base rate for the event to occur, 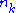 the number of forecasts with the same probability category and
the number of forecasts with the same probability category and 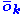 the observed frequency, given forecasts of probability
the observed frequency, given forecasts of probability 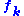 . The bold notation is in the above formula indicates vectors, which is another way of denoting the original definition of the score. For example, a 70% chance of rain and an occurrence of no rain are denoted as
. The bold notation is in the above formula indicates vectors, which is another way of denoting the original definition of the score. For example, a 70% chance of rain and an occurrence of no rain are denoted as  and
and 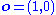 respectively.
respectively.
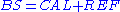
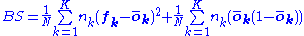
The first term is known as calibration (and can be used as a measure of calibration, see statistical calibration
), as is equal to reliability. The second term is known as refinement, and it is an aggregation of resolution and uncertainty, and is related to the Area Under the ROC Curve).
Scoring rule
In decision theory a score function, or scoring rule, is a measure of the performance of an entity, be it person or machine, that repeatedly makes decisions under uncertainty. For example, every evening a TV weather forecaster may give the probability of rain on the next day, in a type of...
that measures the accuracy of a set of probability
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
assessments. It was proposed by Glenn W. Brier in 1950.
It measures the average squared deviation between predicted probabilities for a set of events and their outcomes, so a lower score represents higher accuracy.
Definition of the Brier score
Nowadays, the most common formulation of the Brier score is
In which
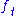 is the probability that was forecast,
is the probability that was forecast, 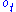 the actual outcome of the event at instance t (0 if it doesn't happen and 1 if it happens) and N is the number of forecasting instances. This formulation is mostly used for binary events (for example "rain" or "no rain").
the actual outcome of the event at instance t (0 if it doesn't happen and 1 if it happens) and N is the number of forecasting instances. This formulation is mostly used for binary events (for example "rain" or "no rain").Example
Suppose it is required to give a probability P forecast of a binary event – such as a forecast of rain. The forecast issued says that there is a probability P that the event will occur. Let X = 1 if the event occurs and X = 0 if it doesn’t.Then the Brier score is given by: .
- If you forecast 100% (P = 1) and there is at least 1 mm of rain in the bucket, your Brier Score is 0, the best score achievable.
- If you forecast 100% P and there is no rain in the bucket, your Brier Score is 1, the worst score achievable.
- If you forecast 70% P and there is at least 1 mm of rain in the bucket, your Brier Score is
 .
. - If you forecast 30% P and there is at least 1 mm of rain in the bucket, your Brier Score is
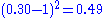 .
. - If you hedge your forecast with a 50% P and whether or not there is at least 1 mm of rain in the bucket, your Brier Score is 0.25.
In weather forecasting, a trace (< 0.01) is considered "0.0"
Original definition by Brier
Although the above formulation is the most widely used. The original definition by Brier was intended to be applicable to multi-category forecasts as well. For binary forecasts the original formulation of Brier's "probability score" has twice the value of the score currently known as the Brier score.
In which R is the number of possible classes in which the event can fall. For the case Rain / No rain, R=2, while for the forecast Cold / Normal / Warm, R=3.
Decompositions
There are several decompositions of the Brier score which provide a deeper insight on the behaviour of a binary classifier.3-component decomposition
The Brier score can be decomposed into 3 additive components: Uncertainty, Reliability and Resolution. (Murphy 1973)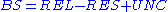
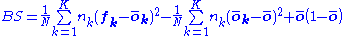
With
 being the total number of forecasts issued,
being the total number of forecasts issued,  the number of unique forecasts issued,
the number of unique forecasts issued, 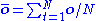 the observed climatological base rate for the event to occur,
the observed climatological base rate for the event to occur, 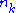 the number of forecasts with the same probability category and
the number of forecasts with the same probability category and 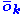 the observed frequency, given forecasts of probability
the observed frequency, given forecasts of probability 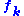 . The bold notation is in the above formula indicates vectors, which is another way of denoting the original definition of the score. For example, a 70% chance of rain and an occurrence of no rain are denoted as
. The bold notation is in the above formula indicates vectors, which is another way of denoting the original definition of the score. For example, a 70% chance of rain and an occurrence of no rain are denoted as  and
and 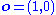 respectively.
respectively.Uncertainty
The uncertainty term measures the inherent uncertainty in the event. For binary events, it is at a maximum when the event occurs 50% of the time and the uncertainty is zero if the event always occurs.Reliability
The reliability term measures how close the forecast probabilities are to the true probabilities, given that forecast. Strangely enough, the reliability is defined in the contrary direction compared to English language. If the reliability is 0, the forecast is perfectly reliable. For example, if we group all forecast instances where 80% chance of rain was forecast, we get a perfect reliability only if it rained 4 out of 5 times after such a forecast was issued.Resolution
The resolution term measures how much the conditional probabilities given the different forecasts differ from the climatic average. The higher this term is the better. In the worst case, when the climatic probability is always forecast, the resolution is zero. In the best case, when the conditional probabilities are zero and one, the resolution is equal to the uncertainty.2-component decomposition
An alternative (and related) decomposition generates two terms instead of three.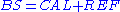
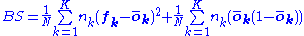
The first term is known as calibration (and can be used as a measure of calibration, see statistical calibration
Calibration (statistics)
There are two main uses of the term calibration in statistics that denote special types of statistical inference problems. Thus "calibration" can mean...
), as is equal to reliability. The second term is known as refinement, and it is an aggregation of resolution and uncertainty, and is related to the Area Under the ROC Curve).

