
Schröder–Hipparchus number
Encyclopedia
In number theory
, the Schröder–Hipparchus numbers form an integer sequence
that can be used to count the number of plane tree
s with a given set of leaves, the number of ways of inserting parentheses into a sequence, and the number of ways of dissecting a convex polygon into smaller polygons by inserting diagonals. These numbers begin
They are also called the super-Catalan numbers, the little Schröder numbers, or the Hipparchus numbers, after Eugène Charles Catalan
and his Catalan number
s, Ernst Schröder
and the closely related Schröder number
s, and the ancient Greek mathematician Hipparchus
who appears from evidence in Plutarch
to have known of these numbers.
As the figure shows, there is a simple combinatorial equivalence between these objects: a polygon subdivision has a plane tree as a form of its dual graph
, the leaves of the tree correspond to the symbols in a parenthesized sequence, and the internal nodes of the tree other than the root correspond to parenthesized groups. The parenthesized sequence itself may be written around the perimeter of the polygon with its symbols on the sides of the polygon and with parentheses at the endpoints of the selected diagonals. This equivalence provides a bijective proof
that all of these kinds of objects are counted by a single integer sequence.
The same numbers also count the number of double permutations (sequences of the numbers from 1 to n, each number appearing twice, with the first occurrences of each number in sorted order) that avoid the permutation pattern
s 12312 and 121323.
are equal to twice the Schröder–Hipparchus numbers, and may also be used to count several types of combinatorial objects including certain kinds of lattice paths, partitions of a rectangle into smaller rectangles by recursive slicing, and parenthesizations in which a pair of parentheses surrounding the whole sequence of elements is also allowed. The Catalan number
s also count closely related sets of objects including subdivisions of a polygon into triangles, plane trees in which all internal nodes have exactly two children, and parenthesizations in which each pair of parentheses surrounds exactly two symbols or parenthesized groups.
The sequence of Catalan numbers and the sequence of Schröder–Hipparchus numbers, viewed as infinite-dimensional vector
s, are the unique eigenvectors for the first two in a sequence of naturally defined linear operators on number sequences. More generally, the kth sequence in this sequence of integer sequences is (x1, x2, x3, ...) where the numbers xn are calculated as the sums of Narayana number
s multiplied by powers of k: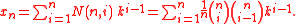
Substituting k = 1 into this formula gives the Catalan numbers and substituting k = 2 into this formula gives the Schröder–Hipparchus numbers.
: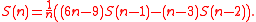
Stanley proves this fact using generating function
s while Foata and Zeilberger provide a direct combinatorial proof.
's Table Talk, Hipparchus showed that the number of "affirmative compound propositions" that can be made from ten simple prepositions is 103049 and that the number of negative compound propositions that can be made from ten simple propositions is 310952. This statement went unexplained until 1994, when David Hough, a graduate student at George Washington University
, observed that there are 103049 ways of inserting parentheses into a sequence of ten items. A similar explanation can be provided for the other number: it is very close to the average of the tenth and eleventh Schröder–Hipparchus numbers, 310954, and counts bracketings of ten terms together with a negative particle.
The problem of counting parenthesizations was introduced to modern mathematics by .
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
, the Schröder–Hipparchus numbers form an integer sequence
Integer sequence
In mathematics, an integer sequence is a sequence of integers.An integer sequence may be specified explicitly by giving a formula for its nth term, or implicitly by giving a relationship between its terms...
that can be used to count the number of plane tree
Tree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
s with a given set of leaves, the number of ways of inserting parentheses into a sequence, and the number of ways of dissecting a convex polygon into smaller polygons by inserting diagonals. These numbers begin
- 1, 1, 3, 11, 45, 197, 903, 4279, 20793, 103049, ... .
They are also called the super-Catalan numbers, the little Schröder numbers, or the Hipparchus numbers, after Eugène Charles Catalan
Eugène Charles Catalan
Eugène Charles Catalan was a French and Belgian mathematician.- Biography :Catalan was born in Bruges , the only child of a French jeweller by the name of Joseph Catalan, in 1814. In 1825, he traveled to Paris and learned mathematics at École Polytechnique, where he met Joseph Liouville...
and his Catalan number
Catalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
s, Ernst Schröder
Ernst Schröder
Ernst Schröder was a German mathematician mainly known for his work on algebraic logic. He is a major figure in the history of mathematical logic , by virtue of summarizing and extending the work of George Boole, Augustus De Morgan, Hugh MacColl, and especially Charles Peirce...
and the closely related Schröder number
Schröder number
In mathematics, a Schröder number describes the number of paths from the southwest corner of an n × n grid to the northeast corner , using only single steps north, northeast, or east, that do not rise above the SW–NE diagonal.The first few Schröder numbers are-Examples:The following...
s, and the ancient Greek mathematician Hipparchus
Hipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
who appears from evidence in Plutarch
Plutarch
Plutarch then named, on his becoming a Roman citizen, Lucius Mestrius Plutarchus , c. 46 – 120 AD, was a Greek historian, biographer, essayist, and Middle Platonist known primarily for his Parallel Lives and Moralia...
to have known of these numbers.
Combinatorial enumeration applications
The Schröder–Hipparchus numbers may be used to count several closely related combinatorial objects:- The nth number in the sequence counts the number of different ways of subdividing of a polygon with n + 1 sides into smaller polygons by adding diagonals of the original polygon.
- The nth number counts the number of different plane treeTree (graph theory)In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
s with n leaves and with all internal vertices having two or more children. - The nth number counts the number of different ways of inserting parentheses into a sequence of n symbols, with each pair of parentheses surrounding two or more symbols or parenthesized groups, and without any parentheses surrounding the entire sequence.
As the figure shows, there is a simple combinatorial equivalence between these objects: a polygon subdivision has a plane tree as a form of its dual graph
Dual graph
In mathematics, the dual graph of a given planar graph G is a graph which has a vertex for each plane region of G, and an edge for each edge in G joining two neighboring regions, for a certain embedding of G. The term "dual" is used because this property is symmetric, meaning that if H is a dual...
, the leaves of the tree correspond to the symbols in a parenthesized sequence, and the internal nodes of the tree other than the root correspond to parenthesized groups. The parenthesized sequence itself may be written around the perimeter of the polygon with its symbols on the sides of the polygon and with parentheses at the endpoints of the selected diagonals. This equivalence provides a bijective proof
Bijective proof
In combinatorics, bijective proof is a proof technique that finds a bijective function f : A → B between two sets A and B, thus proving that they have the same number of elements, |A| = |B|. One place the technique is useful is where we wish to know the size of A, but can find no direct way of...
that all of these kinds of objects are counted by a single integer sequence.
The same numbers also count the number of double permutations (sequences of the numbers from 1 to n, each number appearing twice, with the first occurrences of each number in sorted order) that avoid the permutation pattern
Permutation pattern
In combinatorial mathematics and theoretical computer science, a permutation pattern is a sub-permutation of a longer permutation. The permutation π, written as a word in one-line notation , is said to contain the permutation σ if there exists a subsequence of entries of π that has the same...
s 12312 and 121323.
Related sequences
The closely related large Schröder numbersSchröder number
In mathematics, a Schröder number describes the number of paths from the southwest corner of an n × n grid to the northeast corner , using only single steps north, northeast, or east, that do not rise above the SW–NE diagonal.The first few Schröder numbers are-Examples:The following...
are equal to twice the Schröder–Hipparchus numbers, and may also be used to count several types of combinatorial objects including certain kinds of lattice paths, partitions of a rectangle into smaller rectangles by recursive slicing, and parenthesizations in which a pair of parentheses surrounding the whole sequence of elements is also allowed. The Catalan number
Catalan number
In combinatorial mathematics, the Catalan numbers form a sequence of natural numbers that occur in various counting problems, often involvingrecursively defined objects...
s also count closely related sets of objects including subdivisions of a polygon into triangles, plane trees in which all internal nodes have exactly two children, and parenthesizations in which each pair of parentheses surrounds exactly two symbols or parenthesized groups.
The sequence of Catalan numbers and the sequence of Schröder–Hipparchus numbers, viewed as infinite-dimensional vector
Vector
Vector, a Latin word meaning "carrier", may refer in English to:-In computer science:*A one-dimensional array**Vector , a data type in the C++ Standard Template Library...
s, are the unique eigenvectors for the first two in a sequence of naturally defined linear operators on number sequences. More generally, the kth sequence in this sequence of integer sequences is (x1, x2, x3, ...) where the numbers xn are calculated as the sums of Narayana number
Narayana number
In combinatorics, the Narayana numbers N, n = 1, 2, 3 ..., 1 ≤ k ≤ n, form a triangular array of natural numbers, called Narayana triangle, that occur in various counting problems. They are named for T.V...
s multiplied by powers of k:
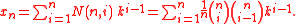
Substituting k = 1 into this formula gives the Catalan numbers and substituting k = 2 into this formula gives the Schröder–Hipparchus numbers.
Recurrence
As well as the summation formula above, the Schröder–Hipparchus numbers may be defined by a recurrence relationRecurrence relation
In mathematics, a recurrence relation is an equation that recursively defines a sequence, once one or more initial terms are given: each further term of the sequence is defined as a function of the preceding terms....
:
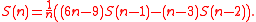
Stanley proves this fact using generating function
Generating function
In mathematics, a generating function is a formal power series in one indeterminate, whose coefficients encode information about a sequence of numbers an that is indexed by the natural numbers. Generating functions were first introduced by Abraham de Moivre in 1730, in order to solve the general...
s while Foata and Zeilberger provide a direct combinatorial proof.
History
According to a line in PlutarchPlutarch
Plutarch then named, on his becoming a Roman citizen, Lucius Mestrius Plutarchus , c. 46 – 120 AD, was a Greek historian, biographer, essayist, and Middle Platonist known primarily for his Parallel Lives and Moralia...
's Table Talk, Hipparchus showed that the number of "affirmative compound propositions" that can be made from ten simple prepositions is 103049 and that the number of negative compound propositions that can be made from ten simple propositions is 310952. This statement went unexplained until 1994, when David Hough, a graduate student at George Washington University
George Washington University
The George Washington University is a private, coeducational comprehensive university located in Washington, D.C. in the United States...
, observed that there are 103049 ways of inserting parentheses into a sequence of ten items. A similar explanation can be provided for the other number: it is very close to the average of the tenth and eleventh Schröder–Hipparchus numbers, 310954, and counts bracketings of ten terms together with a negative particle.
The problem of counting parenthesizations was introduced to modern mathematics by .

