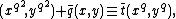Schoof's algorithm
Encyclopedia
Schoof's algorithm is an efficient algorithm to count points on elliptic curves over finite fields. The algorithm has applications in elliptic curve cryptography
where it is important to know the number of points to judge the difficulty of solving the discrete logarithm problem in the group
of points on an elliptic curve.
The algorithm was published by René Schoof in 1985 and it was a theoretical breakthrough, as it was the first deterministic polynomial time algorithm for counting points on elliptic curves
. Before Schoof's algorithm, approaches to counting points on elliptic curves such as the naive and baby-step giant-step
algorithms were, for the most part, tedious and had an exponential running time.
This article explains Schoof's approach, laying emphasis on the mathematical ideas underlying the structure of the algorithm.
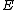 be an elliptic curve
be an elliptic curve
defined over the finite field , where
, where 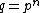 for
for  a prime and
a prime and  an integer
an integer  . Over a field of characteristic
. Over a field of characteristic 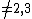 an elliptic curve can be given by a (short) Weierstrass equation
an elliptic curve can be given by a (short) Weierstrass equation
Elliptic curve cryptography
Elliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
where it is important to know the number of points to judge the difficulty of solving the discrete logarithm problem in the group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of points on an elliptic curve.
The algorithm was published by René Schoof in 1985 and it was a theoretical breakthrough, as it was the first deterministic polynomial time algorithm for counting points on elliptic curves
Counting points on elliptic curves
An important aspect in the study of elliptic curves is devising effective ways of counting points on the curve. There have been several approaches to do so, and the algorithms devised have proved to be useful tools in the study of various fields such as number theory, and more recently in...
. Before Schoof's algorithm, approaches to counting points on elliptic curves such as the naive and baby-step giant-step
Baby-step giant-step
In group theory, a branch of mathematics, the baby-step giant-step is a meet-in-the-middle algorithm computing the discrete logarithm. The discrete log problem is of fundamental importance to the area of public key cryptography...
algorithms were, for the most part, tedious and had an exponential running time.
This article explains Schoof's approach, laying emphasis on the mathematical ideas underlying the structure of the algorithm.
Introduction
Let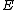 be an elliptic curve
be an elliptic curveElliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
defined over the finite field
 , where
, where 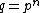 for
for  a prime and
a prime and  an integer
an integer  . Over a field of characteristic
. Over a field of characteristic 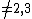 an elliptic curve can be given by a (short) Weierstrass equation
an elliptic curve can be given by a (short) Weierstrass equation
-

with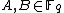 . The set of points defined over
. The set of points defined over 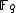 consists of the solutions
consists of the solutions  satisfying the curve equation and a point at infinity
satisfying the curve equation and a point at infinity 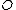 . Using the group law on elliptic curves restricted to this set one can see that this set
. Using the group law on elliptic curves restricted to this set one can see that this set 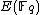 forms an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
forms an abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
, with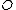 acting as the zero element.
acting as the zero element.
In order to count points on an elliptic curve, we compute the cardinality of .
.
Schoof's approach to computing the cardinality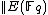 makes use of Hasse's theorem on elliptic curves along with the Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
makes use of Hasse's theorem on elliptic curves along with the Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
and division polynomialsDivision polynomialsIn mathematics the division polynomials provide a way to calculate multiples of points on elliptic curves over Finite fields. They play a central role in the study of counting points on elliptic curves in Schoof's algorithm.- Definition :...
.
Hasse's theorem
Hasse's theorem states that if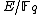 is an elliptic curve over the finite field
is an elliptic curve over the finite field 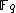 , then
, then 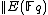 satisfies
satisfies
-

This powerful result, given by Hasse in 1934, simplifies our problem by narrowing down to a finite (albeit large) set of possibilities. Defining
to a finite (albeit large) set of possibilities. Defining  to be
to be 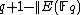 , and making use of this result, we now have that computing the cardinality of
, and making use of this result, we now have that computing the cardinality of  modulo
modulo 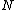 where
where 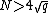 , is sufficient for determining
, is sufficient for determining  , and thus
, and thus 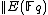 . While there is no efficient way to compute
. While there is no efficient way to compute 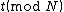 directly for general
directly for general 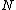 , it is possible to compute
, it is possible to compute 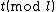 for
for 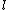 a small prime, rather efficiently. We choose
a small prime, rather efficiently. We choose 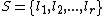 to be a set of distinct primes such that
to be a set of distinct primes such that 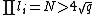 . Given
. Given 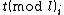 for all
for all 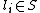 , the Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
, the Chinese remainder theoremChinese remainder theoremThe Chinese remainder theorem is a result about congruences in number theory and its generalizations in abstract algebra.In its most basic form it concerned with determining n, given the remainders generated by division of n by several numbers...
allows us to compute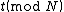 .
.
In order to compute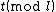 for a prime
for a prime 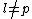 , we make use of the theory of the Frobenius endomorphism
, we make use of the theory of the Frobenius endomorphism 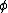 and division polynomialsDivision polynomialsIn mathematics the division polynomials provide a way to calculate multiples of points on elliptic curves over Finite fields. They play a central role in the study of counting points on elliptic curves in Schoof's algorithm.- Definition :...
and division polynomialsDivision polynomialsIn mathematics the division polynomials provide a way to calculate multiples of points on elliptic curves over Finite fields. They play a central role in the study of counting points on elliptic curves in Schoof's algorithm.- Definition :...
. Note that considering primes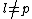 is no loss since we can always pick a bigger prime to take its place to ensure the product is big enough. In any case Schoof's algorithm is most frequently used in addressing the case
is no loss since we can always pick a bigger prime to take its place to ensure the product is big enough. In any case Schoof's algorithm is most frequently used in addressing the case 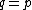 since there are more efficient, so called
since there are more efficient, so called 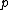 adic algorithms for small characteristic fields.
adic algorithms for small characteristic fields.
The Frobenius endomorphism
Given the elliptic curve defined over
defined over 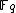 we consider points on
we consider points on 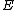 over
over 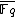 , the algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
, the algebraic closureAlgebraic closureIn mathematics, particularly abstract algebra, an algebraic closure of a field K is an algebraic extension of K that is algebraically closed. It is one of many closures in mathematics....
of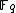 ; i.e. we allow points with coordinates in
; i.e. we allow points with coordinates in 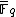 . The Frobenius endomorphismFrobenius endomorphismIn commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class which includes finite fields. The endomorphism maps every element to its pth power...
. The Frobenius endomorphismFrobenius endomorphismIn commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class which includes finite fields. The endomorphism maps every element to its pth power...
of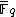 over
over 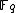 extends to the elliptic curve by
extends to the elliptic curve by 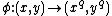 .
.
This map is the identity on and one can extend it to the point at infinity
and one can extend it to the point at infinity 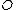 , making it a group morphism from
, making it a group morphism from 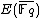 to itself.
to itself.
The Frobenius endomorphism satisfies a quadratic polynomial which is linked to the cardinality of by the following theorem:
by the following theorem:
Theorem: The Frobenius endomorphism given by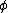 satisfies the characteristic equation
satisfies the characteristic equation
-
 where
where 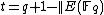
Thus we have for all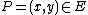 that
that 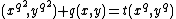 , where + denotes addition on the elliptic curve and
, where + denotes addition on the elliptic curve and  and
and 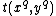
denote scalar multiplication of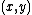 by
by 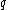 and of
and of 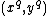 by
by  .
.
One could try to symbolically compute these points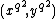 ,
,  and
and 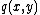 as functions in the coordinate ring
as functions in the coordinate ring  of
of 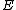
and the search for a value of which satisfies the equation. However, the degrees get very large and this approach is impractical.
which satisfies the equation. However, the degrees get very large and this approach is impractical.
Schoof's idea was to carry out this computation restricted to points of order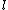 for various small primes
for various small primes 
Fixing an odd prime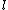 , we now move on to solving the problem of determining
, we now move on to solving the problem of determining  , defined as
, defined as  , for a given prime
, for a given prime 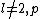 .
.
If a point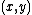 is in the
is in the 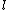 -torsion subgroupTorsion subgroupIn the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
-torsion subgroupTorsion subgroupIn the theory of abelian groups, the torsion subgroup AT of an abelian group A is the subgroup of A consisting of all elements that have finite order...
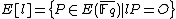 , then
, then 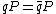 where
where 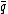 is the unique integer such that
is the unique integer such that  and
and 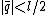 .
.
Note that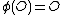 and that for any integer
and that for any integer  we have
we have  . Thus
. Thus 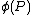 will have the same order as
will have the same order as  . Thus for
. Thus for 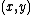 belonging to
belonging to 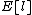 , we also have
, we also have  if
if 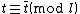 . Hence we have reduced our problem to solving the equation
. Hence we have reduced our problem to solving the equation
where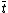 and
and 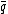 have integer values in
have integer values in 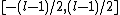 .
.
Computation modulo primes
The th division polynomial is such that its roots are precisely the
th division polynomial is such that its roots are precisely the  coordinates of points of order
coordinates of points of order  . Thus, to restrict the computation of
. Thus, to restrict the computation of 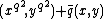 to the
to the 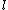 -torsion points means computing these expressions as functions in the coordinate ring of
-torsion points means computing these expressions as functions in the coordinate ring of 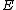 and modulo the
and modulo the  th division polynomial. I.e. we are working in
th division polynomial. I.e. we are working in 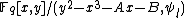 . This means in particular that the degree of
. This means in particular that the degree of 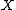 and
and  defined via
defined via  is at most 1 in
is at most 1 in 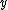 and at most
and at most 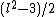
in .
.
The scalar multiplication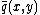 can be done either by double-and-addExponentiation by squaringExponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
can be done either by double-and-addExponentiation by squaringExponentiating by squaring is a general method for fast computation of large integer powers of a number. Some variants are commonly referred to as square-and-multiply algorithms or binary exponentiation. In additive notation the appropriate term is double-and-add...
methods or by using the th division polynomial. The latter approach gives:
th division polynomial. The latter approach gives:
-
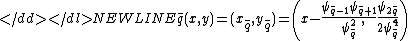
where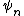 is the
is the  th division polynomial. Note that
th division polynomial. Note that
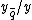 is a function in
is a function in  only and denote it by
only and denote it by 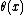 .
.
We must split the problem into two cases: the case in which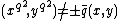 , and the case in which
, and the case in which 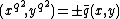 . Note that these equalities are checked modulo
. Note that these equalities are checked modulo  .
.
Case 1:
By using the addition formula for the group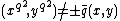
 we obtain:
we obtain:
-
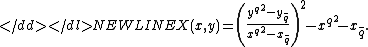
Note that this computation fails in case the assumption of inequality was wrong.
We are now able to use the -coordinate to narrow down the choice of
-coordinate to narrow down the choice of 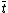 to two possibilities, namely the positive and negative case. Using the
to two possibilities, namely the positive and negative case. Using the 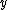 -coordinate one later determines which of the two cases holds.
-coordinate one later determines which of the two cases holds.
We first show that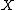 is a function in
is a function in  alone. Consider
alone. Consider 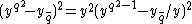 .
.
Since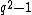 is even, by replacing
is even, by replacing 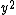 by
by 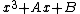 , we rewrite the expression as
, we rewrite the expression as
-
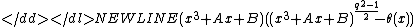
and have that
-
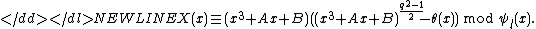
Now if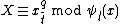 for one
for one 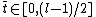 then
then 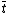 satisfies
satisfies
-
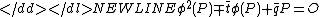
for all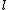 -torsion points
-torsion points 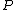 .
.
As mentioned earlier, using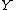 and
and  we are now able to determine which of the two values of
we are now able to determine which of the two values of 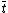 (
(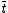 or
or 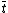 ) works. This gives the value of
) works. This gives the value of 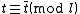 . Schoof's algorithm stores the values of
. Schoof's algorithm stores the values of 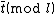 in a variable
in a variable  for each prime
for each prime 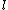 considered.
considered.
Case 2:
We begin with the assumption that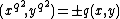
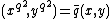 . Since
. Since 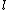 is an odd prime it cannot be that
is an odd prime it cannot be that 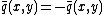 and thus
and thus 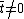 . The characteristic equation yields that
. The characteristic equation yields that 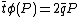 . And consequently that
. And consequently that 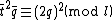 .
.
This implies that is a square modulo
is a square modulo  . Let
. Let 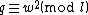 . Compute
. Compute 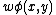 in
in 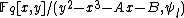 and check whether
and check whether 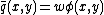 . If so,
. If so, 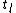 is
is 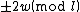 depending on the y-coordinate.
depending on the y-coordinate.
If turns out not to be a square modulo
turns out not to be a square modulo 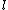 or if the equation does not hold for any of
or if the equation does not hold for any of 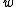 and
and 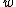 , our assumption that
, our assumption that 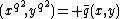 is false, thus
is false, thus 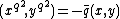 . The characteristic equation gives
. The characteristic equation gives 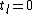 .
.
Additional case:
If you recall, our initial considerations omit the case of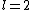
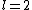 .
.
Since we assume to be odd,
to be odd, 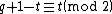 and in particular,
and in particular, 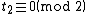 if and only if
if and only if  has an element of order 2. By definition of addition in the group, any element of order 2 must be of the form
has an element of order 2. By definition of addition in the group, any element of order 2 must be of the form 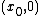 . Thus
. Thus 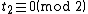 if and only if the polynomial
if and only if the polynomial 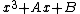 has a root in
has a root in 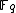 , if and only if
, if and only if 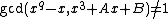 .
.
The algorithm
Choose a set of odd primes ,
, 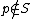 such that
such that 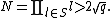 put
put 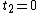 if
if 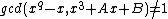 , else
, else 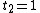 . for
. for  do:
do:
-
- (a) Let
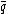 be the unique integer such that
be the unique integer such that 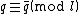 and
and  . Compute
. Compute 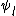 . All following computations in this loop are in the following ring:
. All following computations in this loop are in the following ring: 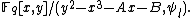
- (b) Compute
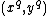 ,
, 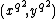 and
and 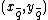 .
. - (c) if
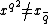 then
then
- (i) compute
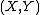 .
. - (ii)for
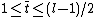 do
do
- (iii)if
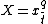 then
then
- (iv)if
 then
then 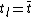 ; else
; else 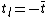 .
.
- (iv)if
- (iii)if
- (i) compute
- (d)else if
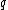 is a square modulo
is a square modulo 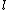 then
then
- (i)compute
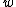 with
with 
- (ii)compute
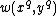
- (iii)if
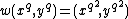 then
then 
- (iv)else if
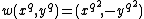 then
then 
- (v)else

- (i)compute
- (e)else
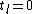 Use the Chinese Remainder Theorem to compute
Use the Chinese Remainder Theorem to compute 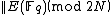 .
.
- (a) Let
Note that since the set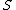 was chosen so that
was chosen so that 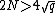 , by Hasse's theorem, we in fact know
, by Hasse's theorem, we in fact know  precisely.
precisely.
Complexity of Schoof's algorithm
Most of the computation is taken by the evaluation of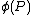 and
and 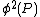 , for each prime
, for each prime 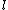 , that is computing
, that is computing 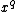 ,
, 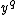 ,
, 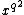 ,
,  for each prime
for each prime 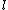 . This involves exponentiation in the ring
. This involves exponentiation in the ring 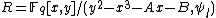 and requires
and requires 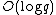 multiplications. Since the degree of
multiplications. Since the degree of  is
is 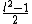 , each element in the ring is a polynomial of degree
, each element in the ring is a polynomial of degree 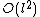 . By the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
. By the prime number theoremPrime number theoremIn number theory, the prime number theorem describes the asymptotic distribution of the prime numbers. The prime number theorem gives a general description of how the primes are distributed amongst the positive integers....
, we have around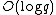 primes of size
primes of size 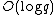 giving that
giving that 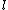 is
is 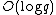 and we obtain that
and we obtain that 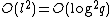 . Thus each multiplication in the ring
. Thus each multiplication in the ring 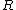 requires
requires 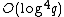 multiplications in
multiplications in 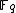 which in turn requires
which in turn requires 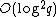 bit operations. In total, the number of bit operations for each prime
bit operations. In total, the number of bit operations for each prime 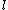 is
is 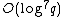 . Given that this computation needs to be carried out for each of the
. Given that this computation needs to be carried out for each of the  primes, the total complexity of Schoof's algorithm turns out to be
primes, the total complexity of Schoof's algorithm turns out to be 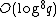 . Note that fast polynomial arithmetic reduces the costs down to
. Note that fast polynomial arithmetic reduces the costs down to  .
.
Improvements to Schoof's algorithm
In the 1990s, Noam ElkiesNoam ElkiesNoam David Elkies is an American mathematician and chess master.At age 14, Elkies received a gold medal with a perfect score at the International Mathematical Olympiad, the youngest ever to do so...
, followed by A. O. L. AtkinA. O. L. AtkinArthur Oliver Lonsdale Atkin , who published under the name A. O. L. Atkin, was a Professor Emeritus of mathematics at the University of Illinois at Chicago. As an undergraduate during World War II, he worked at Bletchley Park cracking German codes. He received his Ph.D...
, devised improvements to Schoof's basic algorithm by restricting the set of primes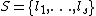 considered before to primes of a certain kind. These came to be called Elkies primes and Atkin primes respectively. A prime
considered before to primes of a certain kind. These came to be called Elkies primes and Atkin primes respectively. A prime 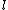 is called an Elkies prime if the characteristic equation:
is called an Elkies prime if the characteristic equation: 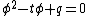 splits over
splits over 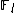 , while an Atkin prime is a prime that is not an Elkies prime. Atkin showed how to combine information obtained from the Atkin primes with the information obtained from Elkies primes to produce an efficient algorithm, which came to be known as the Schoof–Elkies–Atkin algorithm. The first problem to address is to determine whether a given prime is Elkies or Atkin. In order to do so, we make use of modular polynomials, which come from the study of modular forms and an interpretation of elliptic curves over the complex numbers as lattices. Once we have determined which case we are in, instead of using division polynomialsDivision polynomialsIn mathematics the division polynomials provide a way to calculate multiples of points on elliptic curves over Finite fields. They play a central role in the study of counting points on elliptic curves in Schoof's algorithm.- Definition :...
, while an Atkin prime is a prime that is not an Elkies prime. Atkin showed how to combine information obtained from the Atkin primes with the information obtained from Elkies primes to produce an efficient algorithm, which came to be known as the Schoof–Elkies–Atkin algorithm. The first problem to address is to determine whether a given prime is Elkies or Atkin. In order to do so, we make use of modular polynomials, which come from the study of modular forms and an interpretation of elliptic curves over the complex numbers as lattices. Once we have determined which case we are in, instead of using division polynomialsDivision polynomialsIn mathematics the division polynomials provide a way to calculate multiples of points on elliptic curves over Finite fields. They play a central role in the study of counting points on elliptic curves in Schoof's algorithm.- Definition :...
, we proceed by working modulo the modular polynomials which have a lower degree than the corresponding division polynomial
which have a lower degree than the corresponding division polynomial 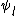 (degree
(degree 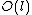 rather than
rather than 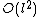 ). This results in a further reduction in the running time, giving us an algorithm more efficient than Schoof's, with complexity
). This results in a further reduction in the running time, giving us an algorithm more efficient than Schoof's, with complexity 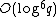 for standard arithmetic and
for standard arithmetic and 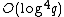 .
.
Implementations
Several algorithms were implemented in C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
by Mike Scott and are available with [ftp://ftp.computing.dcu.ie/pub/crypto/ source code]. The implementations are free (no terms, no conditions), but they use MIRACL library which is only free for non-commercial use. Note that (unmodified) programs may be used to generate curves for commercial use. There are- Schoof's algorithm [ftp://ftp.computing.dcu.ie/pub/crypto/schoof.cpp implementation] for
 with prime
with prime 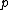 .
. - Schoof's algorithm [ftp://ftp.computing.dcu.ie/pub/crypto/schoof2.cpp implementation] for
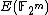 .
.
See also
- Elliptic curve cryptographyElliptic curve cryptographyElliptic curve cryptography is an approach to public-key cryptography based on the algebraic structure of elliptic curves over finite fields. The use of elliptic curves in cryptography was suggested independently by Neal Koblitz and Victor S...
- Counting points on elliptic curvesCounting points on elliptic curvesAn important aspect in the study of elliptic curves is devising effective ways of counting points on the curve. There have been several approaches to do so, and the algorithms devised have proved to be useful tools in the study of various fields such as number theory, and more recently in...
- Division PolynomialsDivision polynomialsIn mathematics the division polynomials provide a way to calculate multiples of points on elliptic curves over Finite fields. They play a central role in the study of counting points on elliptic curves in Schoof's algorithm.- Definition :...
- Frobenius endomorphismFrobenius endomorphismIn commutative algebra and field theory, the Frobenius endomorphism is a special endomorphism of commutative rings with prime characteristic p, an important class which includes finite fields. The endomorphism maps every element to its pth power...
-
-
-
-
-
-
-