
Schnorr group
Encyclopedia
A Schnorr group, proposed by Claus P. Schnorr
, is a large prime-order subgroup
of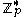 , the multiplicative group of integers modulo
, the multiplicative group of integers modulo 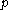
for some prime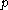 . To generate such a group, generate
. To generate such a group, generate 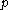 ,
, 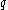 ,
,  such that
such that
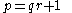
with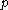 ,
, 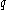 prime. Then choose any
prime. Then choose any 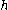 in the range
in the range 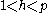 until you find one such that
until you find one such that
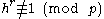 .
.
This value
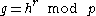
is a generator of a subgroup of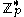 of order
of order 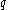 .
.
Schnorr groups are useful in discrete log based cryptosystems including Schnorr signature
s and DSA
. In such applications, typically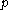 is chosen to be large enough to resist index-calculus and related methods of solving the discrete-log problem (perhaps 1024-2048 bits), while
is chosen to be large enough to resist index-calculus and related methods of solving the discrete-log problem (perhaps 1024-2048 bits), while 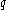 is large enough to resist the birthday attack on discrete log problems, which works in any group (perhaps 160-512 bits). Because the Schnorr group is of prime order, it has no non-trivial proper subgroups, thwarting confinement attacks
is large enough to resist the birthday attack on discrete log problems, which works in any group (perhaps 160-512 bits). Because the Schnorr group is of prime order, it has no non-trivial proper subgroups, thwarting confinement attacks
due to small subgroups. Implementations of protocols that use Schnorr groups must verify where appropriate that integers supplied by other parties are in fact members of the Schnorr group; is a member of the group if
is a member of the group if 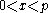 and
and  . Any member of the group except the element
. Any member of the group except the element 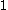 is also a generator of the group.
is also a generator of the group.
See also: Topics in cryptography
Claus P. Schnorr
Claus-Peter Schnorr is a distinguished German mathematician and cryptographer. He received his Ph.D. from the University of Saarbrücken in 1966, and his habilitation in 1970. Schnorr's contributions to cryptography include his study of Schnorr groups, which are used in the digital signature...
, is a large prime-order subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of
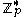 , the multiplicative group of integers modulo
, the multiplicative group of integers modulo 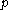
Multiplicative group of integers modulo n
In modular arithmetic the set of congruence classes relatively prime to the modulus n form a group under multiplication called the multiplicative group of integers modulo n. It is also called the group of primitive residue classes modulo n. In the theory of rings, a branch of abstract algebra, it...
for some prime
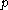 . To generate such a group, generate
. To generate such a group, generate 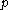 ,
, 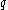 ,
,  such that
such that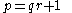
with
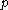 ,
, 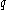 prime. Then choose any
prime. Then choose any 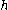 in the range
in the range 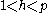 until you find one such that
until you find one such that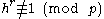 .
.This value
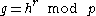
is a generator of a subgroup of
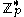 of order
of order 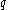 .
.Schnorr groups are useful in discrete log based cryptosystems including Schnorr signature
Schnorr signature
In cryptography, a Schnorr signature is a digital signature produced by the Schnorr signature algorithm. Its security is based on the intractability of certain discrete logarithm problems. It is considered the simplest digital signature scheme to be provably secure in a random oracle model . It is...
s and DSA
Digital Signature Algorithm
The Digital Signature Algorithm is a United States Federal Government standard or FIPS for digital signatures. It was proposed by the National Institute of Standards and Technology in August 1991 for use in their Digital Signature Standard , specified in FIPS 186, adopted in 1993. A minor...
. In such applications, typically
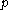 is chosen to be large enough to resist index-calculus and related methods of solving the discrete-log problem (perhaps 1024-2048 bits), while
is chosen to be large enough to resist index-calculus and related methods of solving the discrete-log problem (perhaps 1024-2048 bits), while 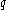 is large enough to resist the birthday attack on discrete log problems, which works in any group (perhaps 160-512 bits). Because the Schnorr group is of prime order, it has no non-trivial proper subgroups, thwarting confinement attacks
is large enough to resist the birthday attack on discrete log problems, which works in any group (perhaps 160-512 bits). Because the Schnorr group is of prime order, it has no non-trivial proper subgroups, thwarting confinement attacksSmall subgroup confinement attack
In cryptography, a subgroup confinement attack on a cryptographic method that operates in a large finite group is where an attacker attempts to compromise the method by forcing a key to be confined to an unexpectedly small subgroup of the desired group.Several methods have been found to be...
due to small subgroups. Implementations of protocols that use Schnorr groups must verify where appropriate that integers supplied by other parties are in fact members of the Schnorr group;
 is a member of the group if
is a member of the group if 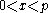 and
and  . Any member of the group except the element
. Any member of the group except the element 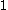 is also a generator of the group.
is also a generator of the group.See also: Topics in cryptography

