In the theory of general relativity

General relativity

General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...

, and differential geometry more generally, Schild's ladder is a first-order method for approximating parallel transport

Parallel transport

In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...

 of a vector along a curve using only affinely parametrized geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

s. The method is named for Alfred Schild

Alfred Schild

Alfred Schild was a leading American physicist, well-known for his contributions to the Golden age of general relativity ....

, who introduced the method during lectures at Princeton University

Princeton University

Princeton University is a private research university located in Princeton, New Jersey, United States. The school is one of the eight universities of the Ivy League, and is one of the nine Colonial Colleges founded before the American Revolution....

.

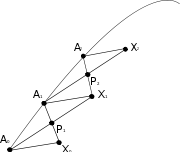
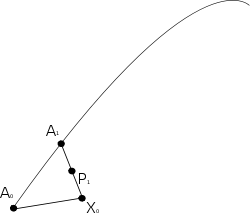
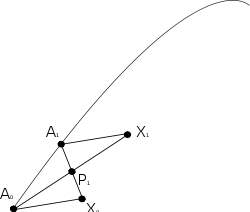
Construction

The idea is to identify a tangent vector x at a point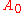 with a geodesic segment of unit length 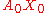, and to construct an approximate parallelogram with approximately parallel sides 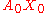and 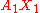as an approximation of the Levi-Civita parallelogramoid

Levi-Civita parallelogramoid

In the mathematical field of differential geometry, the Levi-Civita parallelogramoid is a certain figure generalizing a parallelogram to a curved space. It is named for its discoverer, Tullio Levi-Civita...

; the new segment 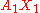thus corresponds to an approximately parallel translated tangent vector at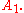


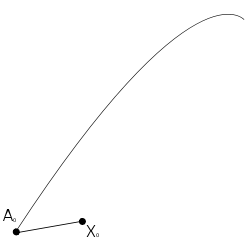
Formally, consider a curve γ through a point A₀ in a Riemannian manifold

Riemannian manifold

In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...

 M, and let x be a tangent vector

Tangent vector

A tangent vector is a vector that is tangent to a curve or surface at a given point.Tangent vectors are described in the differential geometry of curves in the context of curves in Rn. More generally, tangent vectors are elements of a tangent space of a differentiable manifold....

 at A₀. Then x can be identified with a geodesic segment A₀X₀ via the exponential map

Exponential map

In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....

. This geodesic σ satisfies


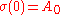
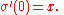
The steps of the Schild's ladder construction are:

• Let X₀ = σ(1), so the geodesic segment 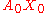has unit length.
• Now let A₁ be a point on γ close to A₀, and construct the geodesic X₀A₁.
• Let P₁ be the midpoint of X₀A₁ in the sense that the segments X₀P₁ and P₁A₁ take an equal affine parameter to traverse.
• Construct the geodesic A₀P₁, and extend it to a point X₁ so that the parameter length of A₀X₁ is double that of A₀P₁.
• Finally construct the geodesic A₁X₁. The tangent to this geodesic x₁ is then the parallel transport of X₀ to A₁, at least to first order.

Approximation

This is a discrete approximation of the continuous process of parallel transport. If the ambient space is flat, this is exactly parallel transport, and the steps define parallelograms, which agree with the Levi-Civita parallelogramoid

Levi-Civita parallelogramoid

In the mathematical field of differential geometry, the Levi-Civita parallelogramoid is a certain figure generalizing a parallelogram to a curved space. It is named for its discoverer, Tullio Levi-Civita...

.

In a curved space, the error is given by holonomy

Holonomy

In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...

 around the triangle which is equal to the integral of the curvature

Curvature

In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...

 over the interior of the triangle, by the Ambrose-Singer theorem; this is a form of Green's theorem

Green's theorem

In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...

(integral around a curve related to integral over interior).