
Sard's lemma
Encyclopedia
Sard's theorem, also known as Sard's lemma or the Morse–Sard theorem, is a result in mathematical analysis
which asserts that the image
of the set of critical point
s of a smooth function
f from one Euclidean space
or manifold
to another has Lebesgue measure
0 – they form a null set
. This makes it "small" in the sense of a generic property
.
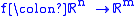
be Ck, k times continuously differentiable, where k ≥ max{n−m+1, 1}. Let X be the critical set of f, the set of points x in Rn at which the Jacobian matrix of f has rank < m. Then f(X) has Lebesgue measure 0 in Rm.
Thus although X itself may be large, its image must be small: f may have many critical points (in the domain Rn), it has few critical values (in the target space Rm).
More generally, the result also holds for mappings between second countable
differentiable manifold
s M and N of dimensions m and n, respectively. The critical set X of a Ck function f : N → M consists of those points at which the differential df : TN → TM has rank less than m as a linear transformation. If k ≥ max{n−m+1, 1}, then Sard's theorem asserts that the image of X has measure zero as a subset of M. This formulation of the result follows from the version for Euclidean spaces by taking a countable set of coordinate patches. The conclusion of the theorem is a local statement, since a countable union of sets of measure zero is a set of measure zero, and the property of a subset of a coordinate patch having zero measure is invariant under diffeomorphism
.
among other fields. The case m = 1 was proven by Anthony P. Morse in 1939 , and the general case by Arthur Sard in 1942 .
A version for infinite-dimensional Banach manifold
s was proven by Stephen Smale
.
The statement is quite powerful, and the proof is involved analysis. In topology it is often quoted — as in the Brouwer fixed point theorem
and some applications in Morse theory
— in order to use the weaker corollary that “a non-constant smooth map has a regular value”, and sometimes “...hence also a regular point”.
In 1965 Sard further generalized his theorem to state that if f : M → N is Ck for k ≥ max{n−m+1, 1} and if Ar ⊆ M is the set of points x ∈ M such that dfx has rank less than or equal to r then f(Ar) has Hausdorff dimension
at most r.
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
which asserts that the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of the set of critical point
Critical point (mathematics)
In calculus, a critical point of a function of a real variable is any value in the domain where either the function is not differentiable or its derivative is 0. The value of the function at a critical point is a critical value of the function...
s of a smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
f from one Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
or manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
to another has Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
0 – they form a null set
Null set
In mathematics, a null set is a set that is negligible in some sense. For different applications, the meaning of "negligible" varies. In measure theory, any set of measure 0 is called a null set...
. This makes it "small" in the sense of a generic property
Generic property
In mathematics, properties that hold for "typical" examples are called generic properties. For instance, a generic property of a class of functions is one that is true of "almost all" of those functions, as in the statements, "A generic polynomial does not have a root at zero," or "A generic...
.
Statement
More explicitly , let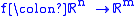
be Ck, k times continuously differentiable, where k ≥ max{n−m+1, 1}. Let X be the critical set of f, the set of points x in Rn at which the Jacobian matrix of f has rank < m. Then f(X) has Lebesgue measure 0 in Rm.
Thus although X itself may be large, its image must be small: f may have many critical points (in the domain Rn), it has few critical values (in the target space Rm).
More generally, the result also holds for mappings between second countable
Second-countable space
In topology, a second-countable space, also called a completely separable space, is a topological space satisfying the second axiom of countability. A space is said to be second-countable if its topology has a countable base...
differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
s M and N of dimensions m and n, respectively. The critical set X of a Ck function f : N → M consists of those points at which the differential df : TN → TM has rank less than m as a linear transformation. If k ≥ max{n−m+1, 1}, then Sard's theorem asserts that the image of X has measure zero as a subset of M. This formulation of the result follows from the version for Euclidean spaces by taking a countable set of coordinate patches. The conclusion of the theorem is a local statement, since a countable union of sets of measure zero is a set of measure zero, and the property of a subset of a coordinate patch having zero measure is invariant under diffeomorphism
Diffeomorphism
In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.- Definition :...
.
Variants
There are many variants of this lemma, which plays a basic role in singularity theorySingularity theory
-The notion of singularity:In mathematics, singularity theory is the study of the failure of manifold structure. A loop of string can serve as an example of a one-dimensional manifold, if one neglects its width. What is meant by a singularity can be seen by dropping it on the floor...
among other fields. The case m = 1 was proven by Anthony P. Morse in 1939 , and the general case by Arthur Sard in 1942 .
A version for infinite-dimensional Banach manifold
Banach manifold
In mathematics, a Banach manifold is a manifold modeled on Banach spaces. Thus it is a topological space in which each point has a neighbourhood homeomorphic to an open set in a Banach space...
s was proven by Stephen Smale
Stephen Smale
Steven Smale a.k.a. Steve Smale, Stephen Smale is an American mathematician from Flint, Michigan. He was awarded the Fields Medal in 1966, and spent more than three decades on the mathematics faculty of the University of California, Berkeley .-Education and career:He entered the University of...
.
The statement is quite powerful, and the proof is involved analysis. In topology it is often quoted — as in the Brouwer fixed point theorem
Brouwer fixed point theorem
Brouwer's fixed-point theorem is a fixed-point theorem in topology, named after Luitzen Brouwer. It states that for any continuous function f with certain properties there is a point x0 such that f = x0. The simplest form of Brouwer's theorem is for continuous functions f from a disk D to...
and some applications in Morse theory
Morse theory
In differential topology, the techniques of Morse theory give a very direct way of analyzing the topology of a manifold by studying differentiable functions on that manifold. According to the basic insights of Marston Morse, a differentiable function on a manifold will, in a typical case, reflect...
— in order to use the weaker corollary that “a non-constant smooth map has a regular value”, and sometimes “...hence also a regular point”.
In 1965 Sard further generalized his theorem to state that if f : M → N is Ck for k ≥ max{n−m+1, 1} and if Ar ⊆ M is the set of points x ∈ M such that dfx has rank less than or equal to r then f(Ar) has Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
at most r.
See also
- Jacobian criterion / generic smoothness, similar statements in algebraic geometryAlgebraic geometryAlgebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...

