Sammon's projection
Encyclopedia
Sammon projection or Sammon mapping is an algorithm that maps
a high-dimensional space to a space of lower dimensionality (see multidimensional scaling
) by trying to preserve the structure of inter-point distances in high-dimensional space in the lower-dimension projection. It is particularly suited for use in exploratory data analysis
. The method was proposed by John W. Sammon in 1969. It is considered a non-linear approach as the projection cannot be represented as a linear combination of the original variables as possible in techniques such as principal component analysis, which also makes it more difficult to use for classification applications.
Denote the distance between ith and jth objects in the original space by
, and the distance between their projections by 
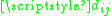. Sammon's projection aims to minimize the following error function, which is often referred to as Sammon's stress:
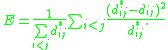
The minimization can be performed either by gradient descent
, as proposed initially, or by other means, usually involving iterative methods. The number of iterations need to be experimentally determined and convergent solutions are not always guaranteed. Many implementations prefer to use the first Principal Components as a starting configuration.
The Sammon mapping has been one of the most successful nonlinear metric multidimensional scaling methods since its advent in 1969, but effort has been focused on algorithm improvement rather than on the form of the stress function. The performance of the Sammon mapping has been improved by extending its stress function using left Bregman divergence
and right Bregman divergence.
Map (mathematics)
In most of mathematics and in some related technical fields, the term mapping, usually shortened to map, is either a synonym for function, or denotes a particular kind of function which is important in that branch, or denotes something conceptually similar to a function.In graph theory, a map is a...
a high-dimensional space to a space of lower dimensionality (see multidimensional scaling
Multidimensional scaling
Multidimensional scaling is a set of related statistical techniques often used in information visualization for exploring similarities or dissimilarities in data. MDS is a special case of ordination. An MDS algorithm starts with a matrix of item–item similarities, then assigns a location to each...
) by trying to preserve the structure of inter-point distances in high-dimensional space in the lower-dimension projection. It is particularly suited for use in exploratory data analysis
Exploratory data analysis
In statistics, exploratory data analysis is an approach to analysing data sets to summarize their main characteristics in easy-to-understand form, often with visual graphs, without using a statistical model or having formulated a hypothesis...
. The method was proposed by John W. Sammon in 1969. It is considered a non-linear approach as the projection cannot be represented as a linear combination of the original variables as possible in techniques such as principal component analysis, which also makes it more difficult to use for classification applications.
Denote the distance between ith and jth objects in the original space by
, and the distance between their projections by 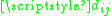. Sammon's projection aims to minimize the following error function, which is often referred to as Sammon's stress: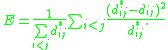The minimization can be performed either by gradient descent
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
, as proposed initially, or by other means, usually involving iterative methods. The number of iterations need to be experimentally determined and convergent solutions are not always guaranteed. Many implementations prefer to use the first Principal Components as a starting configuration.
The Sammon mapping has been one of the most successful nonlinear metric multidimensional scaling methods since its advent in 1969, but effort has been focused on algorithm improvement rather than on the form of the stress function. The performance of the Sammon mapping has been improved by extending its stress function using left Bregman divergence
and right Bregman divergence.