
SKI combinator calculus
Encyclopedia
SKI combinator calculus is a computational system
that may be perceived as a reduced version of untyped lambda calculus
. It can be thought of as a computer programming language, though it is not useful for writing software. Instead, it is important in the mathematical theory of algorithms
because it is an extremely simple Turing complete language.
All operations in lambda calculus are expressed in SKI as binary trees whose leaves are one of the three symbols S, K, and I (called combinators). In fact, the symbol I is added only for convenience, and just the other two suffice for all of the purposes of the SKI system.
Although the most formal representation of the objects in this system requires binary trees, they are usually represented, for typesetability, as parenthesized expressions, either with all the subtrees parenthesized, or only the right-side children subtrees parenthesized. So, the tree whose left subtree is the tree KS and whose right subtree is the tree SK is usually typed as ((KS)(SK)), or more simply as KS(SK), instead of being fully drawn as a tree (as formality and readability would require).
"argument" y. When "evaluated" (i.e., when the function is "applied" to the argument), the tree "returns a value", i.e., transforms into another tree. Of course, all three of the "function", the "argument" and the "value" are either combinators, or binary trees, and if they are binary trees they too may be thought of as functions whenever the need arises.
The evaluation operation is defined as follows:
(x, y, and z represent expressions made from the functions S, K, and I, and set values):
I returns its argument:
K, when applied to any argument x, yields a one-argument constant function Kx , which, when applied to any argument, returns x:
S is a substitution operator. It takes three arguments and then returns the first argument applied to the third, which is then applied to the result of the second argument applied to the third. More clearly:
Example computation: SKSK evaluates to KK(SK) by the S-rule. Then if we evaluate KK(SK), we get K by the K-rule. As no further rule can be applied, the computation halts here.
Note that, for all trees x and all trees y, SKxy will always evaluate to y in two steps, Ky(xy) = y, so the ultimate result of evaluating SKxy will always equal the result of evaluating y. We say that SKx and I are "functionally equivalent" because they always yield the same result when applied to any y.
Note that from these definitions it can be shown that SKI calculus is not the minimum system that can fully perform the computations of lambda calculus, as all occurrences of I in any expression can be replaced by (SKK) or (SKS) or (SK whatever) and the resulting expression will yield the same result. So the "I" is merely syntactic sugar
.
In fact, it is possible to define a complete system using only one combinator. An example is Chris Barker's iota
combinator, defined as follows:
Terms:
The set T of terms is defined recursively by the following rules. If τ1 and τ2 are terms, then (τ1τ2) is a term.
Nothing is a term if not required to be so by the first two rules.
Derivations:
A derivation is a finite sequence of terms defined recursively by the following rules (where all Greek letters represent valid terms or expressions with fully balanced parentheses): If Δ is a derivation ending in an expression of the form α(( Kβ)γ)ι, then Δ followed by the term αβι is a derivation.
If Δ is a derivation ending in an expression of the form α((( Sβ)γ)δ)ι, then Δ followed by the term α((βδ)(γδ))ι is a derivation.
Assuming a sequence is a valid derivation to begin with, it can be extended using these rules. http://people.cs.uchicago.edu/~odonnell/Teacher/Lectures/Formal_Organization_of_Knowledge/Examples/combinator_calculus/
One interesting property of this is that it makes the expression SII(SII) irreducible:
Another thing that results from this is that it allows you to write a function that applies something to the self application of something else:
This function can be used to achieve recursion
. If β is the function that applies α to the self application of something else, then self-applying β performs α recursively on ββ. More clearly, if:
then:
K(SI)α(Kα)β →
SI(Kα)β →
Iβ(Kαβ) →
Iβα
βα
in the form of an if-then-else structure. An if-then-else structure consists of a Boolean expression that is either true (T) or false (F) and two arguments, such that:
and
The key is in defining the two Boolean expressions. The first works just like one of our basic combinators:
The second is also fairly simple:
Once true and false are defined, all Boolean logic can be implemented in terms of if-then-else structures.
Boolean NOT (which returns the opposite of a given Boolean) works the same as the if-then-else structure, with F and T as the second and third values, so it can be implemented as a postfix operation:
If this is put in an if-then-else structure, it can be shown that this has the expected result
Boolean OR (which returns T if either of the two Boolean values surrounding it is T) works the same as an if-then-else structure with T as the second value, so it can be implemented as an infix operation:
If this is put in an if-then-else structure, it can be shown that this has the expected result:
Boolean AND (which returns T if both of the two Boolean values surrounding it are T) works the same as an if-then-else structure with F as the third value, so it can be implemented as a postfix operation:
If this is put in an if-then-else structure, it can be shown that this has the expected result:
Because this defines T, F, NOT (as a postfix operator), OR (as an infix operator), and AND (as a postfix operator) in terms of SKI notation, this proves that the SKI system can fully express Boolean logic.
AK: A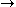 (B
(B 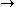 A),
A),
AS: (A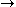 (B
(B 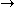 C))
C)) 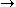 ((A
((A 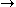 B)
B) 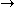 (A
(A 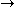 C)).
C)).
Function application corresponds to the rule modus ponens
:
MP: from A and A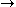 B, infer B.
B, infer B.
The axioms AK and AS, and the rule MP are complete for the implicational fragment of intuitionistic logic
. In order for combinatory logic to have as a model:
Model of computation
In computability theory and computational complexity theory, a model of computation is the definition of the set of allowable operations used in computation and their respective costs...
that may be perceived as a reduced version of untyped lambda calculus
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
. It can be thought of as a computer programming language, though it is not useful for writing software. Instead, it is important in the mathematical theory of algorithms
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
because it is an extremely simple Turing complete language.
All operations in lambda calculus are expressed in SKI as binary trees whose leaves are one of the three symbols S, K, and I (called combinators). In fact, the symbol I is added only for convenience, and just the other two suffice for all of the purposes of the SKI system.
Although the most formal representation of the objects in this system requires binary trees, they are usually represented, for typesetability, as parenthesized expressions, either with all the subtrees parenthesized, or only the right-side children subtrees parenthesized. So, the tree whose left subtree is the tree KS and whose right subtree is the tree SK is usually typed as ((KS)(SK)), or more simply as KS(SK), instead of being fully drawn as a tree (as formality and readability would require).
Informal description
Informally, and using programming language jargon, a tree (xy) can be thought of as a "function" x applied to an"argument" y. When "evaluated" (i.e., when the function is "applied" to the argument), the tree "returns a value", i.e., transforms into another tree. Of course, all three of the "function", the "argument" and the "value" are either combinators, or binary trees, and if they are binary trees they too may be thought of as functions whenever the need arises.
The evaluation operation is defined as follows:
(x, y, and z represent expressions made from the functions S, K, and I, and set values):
I returns its argument:
- Ix = x
K, when applied to any argument x, yields a one-argument constant function Kx , which, when applied to any argument, returns x:
- Kxy = x
S is a substitution operator. It takes three arguments and then returns the first argument applied to the third, which is then applied to the result of the second argument applied to the third. More clearly:
Example computation: SKSK evaluates to KK(SK) by the S-rule. Then if we evaluate KK(SK), we get K by the K-rule. As no further rule can be applied, the computation halts here.
Note that, for all trees x and all trees y, SKxy will always evaluate to y in two steps, Ky(xy) = y, so the ultimate result of evaluating SKxy will always equal the result of evaluating y. We say that SKx and I are "functionally equivalent" because they always yield the same result when applied to any y.
Note that from these definitions it can be shown that SKI calculus is not the minimum system that can fully perform the computations of lambda calculus, as all occurrences of I in any expression can be replaced by (SKK) or (SKS) or (SK whatever) and the resulting expression will yield the same result. So the "I" is merely syntactic sugar
Syntactic sugar
Syntactic sugar is a computer science term that refers to syntax within a programming language that is designed to make things easier to read or to express....
.
In fact, it is possible to define a complete system using only one combinator. An example is Chris Barker's iota
Iota and Jot
Iota and its successor Jot are Turing tarpits, esoteric programming languages that are designed to be as small as possible but still Turing-complete. Each uses two symbols and involves two operations, with simple denotational semantics defined in terms of lambda calculus...
combinator, defined as follows:
- ιx = xSK
Formal definition
The terms and derivations in this system can also be more formally defined:Terms:
The set T of terms is defined recursively by the following rules.
Derivations:
A derivation is a finite sequence of terms defined recursively by the following rules (where all Greek letters represent valid terms or expressions with fully balanced parentheses):
- If Δ is a derivation ending in an expression of the form α(
Assuming a sequence is a valid derivation to begin with, it can be extended using these rules. http://people.cs.uchicago.edu/~odonnell/Teacher/Lectures/Formal_Organization_of_Knowledge/Examples/combinator_calculus/
Self-application and recursion
SII is an expression that takes an argument and applies that argument to itself:One interesting property of this is that it makes the expression SII(SII) irreducible:
Another thing that results from this is that it allows you to write a function that applies something to the self application of something else:
- (
This function can be used to achieve recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
. If β is the function that applies α to the self application of something else, then self-applying β performs α recursively on ββ. More clearly, if:
- β =
then:

The reversal expression
S(K(SI))K reverses the following two terms:Boolean logic
SKI combinator calculus can also implement Boolean logicBoolean logic
Boolean algebra is a logical calculus of truth values, developed by George Boole in the 1840s. It resembles the algebra of real numbers, but with the numeric operations of multiplication xy, addition x + y, and negation −x replaced by the respective logical operations of...
in the form of an if-then-else structure. An if-then-else structure consists of a Boolean expression that is either true (T) or false (F) and two arguments, such that:
and
- Fxy = y
The key is in defining the two Boolean expressions. The first works just like one of our basic combinators:
- T = K
- Kxy = x
The second is also fairly simple:
- F = KI
- KIxy = Iy = y
Once true and false are defined, all Boolean logic can be implemented in terms of if-then-else structures.
Boolean NOT (which returns the opposite of a given Boolean) works the same as the if-then-else structure, with F and T as the second and third values, so it can be implemented as a postfix operation:
- NOT = (F)(T) = (KI)(K)
If this is put in an if-then-else structure, it can be shown that this has the expected result
- (T)NOT = T(F)(T) = F
- (F)NOT = F(F)(T) = T
Boolean OR (which returns T if either of the two Boolean values surrounding it is T) works the same as an if-then-else structure with T as the second value, so it can be implemented as an infix operation:
- OR = T = K
If this is put in an if-then-else structure, it can be shown that this has the expected result:
- (T)OR(T) = T(T)(T) = T
- (T)OR(F) = T(T)(F) = T
- (F)OR(T) = F(T)(T) = T
- (F)OR(F) = F(T)(F) = F
Boolean AND (which returns T if both of the two Boolean values surrounding it are T) works the same as an if-then-else structure with F as the third value, so it can be implemented as a postfix operation:
- AND = F = KI
If this is put in an if-then-else structure, it can be shown that this has the expected result:
- (T)(T)AND = T(T)(F) = T
- (T)(F)AND = T(F)(F) = F
- (F)(T)AND = F(T)(F) = F
- (F)(F)AND = F(F)(F) = F
Because this defines T, F, NOT (as a postfix operator), OR (as an infix operator), and AND (as a postfix operator) in terms of SKI notation, this proves that the SKI system can fully express Boolean logic.
Connection to intuitionistic logic
The combinators K and S correspond to two well-known axioms of sentential logic:AK: A
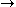 (B
(B 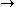 A),
A),AS: (A
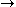 (B
(B 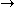 C))
C)) 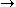 ((A
((A 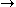 B)
B) 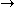 (A
(A  C)).
C)).Function application corresponds to the rule modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
:
MP: from A and A
 B, infer B.
B, infer B.The axioms AK and AS, and the rule MP are complete for the implicational fragment of intuitionistic logic
Intuitionistic logic
Intuitionistic logic, or constructive logic, is a symbolic logic system differing from classical logic in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either...
. In order for combinatory logic to have as a model:
- The implicational fragmentImplicational propositional calculusIn mathematical logic, the implicational propositional calculus is a version of classical propositional calculus which uses only one connective, called implication or conditional...
of classical logicClassical logicClassical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
, would require the combinatory analog to the law of excluded middleLaw of excluded middleIn logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
, e.g., Peirce's lawPeirce's lawIn logic, Peirce's law is named after the philosopher and logician Charles Sanders Peirce. It was taken as an axiom in his first axiomatisation of propositional logic. It can be thought of as the law of excluded middle written in a form that involves only one sort of connective, namely...
; - Complete classical logic, would require the combinatory analog to the sentential axiom F
 A.
A.
See also
- Combinatory logicCombinatory logicCombinatory logic is a notation introduced by Moses Schönfinkel and Haskell Curry to eliminate the need for variables in mathematical logic. It has more recently been used in computer science as a theoretical model of computation and also as a basis for the design of functional programming...
- B,C,K,W systemB,C,K,W systemThe B, C, K, W system is a variant of combinatory logic that takes as primitive the combinators B, C, K, and W. This system was discovered by Haskell Curry in his doctoral thesis Grundlagen der kombinatorischen Logik, whose results are set out in Curry .The combinators are defined as follows:* B x...
- Fixed point combinatorFixed point combinatorIn computer science, a fixed-point combinator is a higher-order function that computes a fixed point of other functions. A fixed point of a function f is a value x such that x = f. For example, 0 and 1 are fixed points of the function f = x2, because 0 = 02 and 1 = 12...
- Lambda calculusLambda calculusIn mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
- Functional programmingFunctional programmingIn computer science, functional programming is a programming paradigm that treats computation as the evaluation of mathematical functions and avoids state and mutable data. It emphasizes the application of functions, in contrast to the imperative programming style, which emphasizes changes in state...
- UnlambdaUnlambdaUnlambda is a minimal, "nearly pure" functional programming language invented by David Madore. It is based on combinatory logic, a version of the lambda calculus that omits the lambda operator. It relies mainly on two built-in functions and an "apply" operator...
programming language - To Mock a MockingbirdTo Mock a MockingbirdTo Mock a Mockingbird and Other Logic Puzzles: Including an Amazing Adventure in Combinatory Logic is a book by the mathematician and logician Raymond Smullyan. It contains many nontrivial recreational puzzles of the sort for which Smullyan is well-known...
External links
- O'Donnell, Mike "The SKI Combinator Calculus as a Universal System."
- Keenan, David C. (2001) "To Dissect a Mockingbird."
- Rathman, Chris, "Combinator Birds."
- ""Drag 'n' Drop Combinators (Java Applet)."

