Rota–Baxter algebra
Encyclopedia
In mathematics
, a Rota–Baxter algebra is an algebra
, usually over a field
k, together with a particular k-linear map R which satisfies the weight-θ Rota–Baxter identity. It appeared first in the work of the American mathematician Glen Baxter
in the realm of probability theory
. Baxter's work was further explored from different angles by Gian-Carlo Rota
, Pierre Cartier
, and Frederic V. Atkinson, among others. Baxter’s derivation of this identity that later bore his name emanated from some of the fundamental results of the famous probabilist Frank Spitzer
in random walk theory.
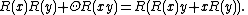
The operator R:= θ id − R also satisfies the Rota–Baxter relation of weight θ.
Integration by parts
is an example of a Rota–Baxter algebra of weight 0. Let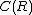
be the algebra of continuous functions from the real line to the real line. Let :
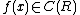be a continuous function. Define integration
as the Rota–Baxter operator
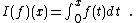
Let G(x) = I(g)(x) and F(x) = I(f)(x). Then the formula for integration for parts can be written in terms of these variables as
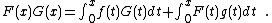
In other words
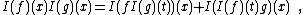
which shows that I is a Rota–Baxter algebra of weight 0.
. It is regarded as a remarkable
stepping stone in the theory of sums of independent random variables in fluctuation theory of probability. It can naturally be understood in terms of Rota–Baxter operators.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a Rota–Baxter algebra is an algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
, usually over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
k, together with a particular k-linear map R which satisfies the weight-θ Rota–Baxter identity. It appeared first in the work of the American mathematician Glen Baxter
Glen Baxter (mathematician)
Glen Earl Baxter was an American mathematician.Baxter's fields of research include probability theory, combinatorial analysis, statistical mechanics and functional analysis...
in the realm of probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
. Baxter's work was further explored from different angles by Gian-Carlo Rota
Gian-Carlo Rota
Gian-Carlo Rota was an Italian-born American mathematician and philosopher.-Life:Rota was born in Vigevano, Italy...
, Pierre Cartier
Pierre Cartier (mathematician)
Pierre Cartier is a mathematician. An associate of the Bourbaki group and at one time a colleague of Alexander Grothendieck, his interests have ranged over algebraic geometry, representation theory, mathematical physics, and category theory....
, and Frederic V. Atkinson, among others. Baxter’s derivation of this identity that later bore his name emanated from some of the fundamental results of the famous probabilist Frank Spitzer
Frank Spitzer
Frank Ludvig Spitzer was an Austrian-born American mathematician who made fundamental contributions to probability theory, including the theory of random walks, fluctuation theory, percolation theory, the Wiener sausage, and especially the theory of interacting particle systems...
in random walk theory.
Definition and first properties
Let A be a k-algebra with a k-linear map R on A and let θ be a fixed parameter in k. We call A a Rota-Baxter k-algebra and R a Rota-Baxter operator of weight θ if the operator R satisfies the following Rota–Baxter relation of weight θ: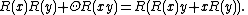The operator R:= θ id − R also satisfies the Rota–Baxter relation of weight θ.
Examples
Integration by PartsIntegration by parts
Integration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
is an example of a Rota–Baxter algebra of weight 0. Let
be the algebra of continuous functions from the real line to the real line. Let :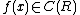 be a continuous function. Define integrationIntegral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
as the Rota–Baxter operator
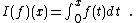
Let G(x) = I(g)(x) and F(x) = I(f)(x). Then the formula for integration for parts can be written in terms of these variables as
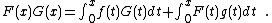
In other words
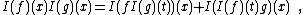
which shows that I is a Rota–Baxter algebra of weight 0.
Spitzer identity
The Spitzer identity appeared is named after the American mathematician Frank SpitzerFrank Spitzer
Frank Ludvig Spitzer was an Austrian-born American mathematician who made fundamental contributions to probability theory, including the theory of random walks, fluctuation theory, percolation theory, the Wiener sausage, and especially the theory of interacting particle systems...
. It is regarded as a remarkable
stepping stone in the theory of sums of independent random variables in fluctuation theory of probability. It can naturally be understood in terms of Rota–Baxter operators.
External links
- Li Guo. WHAT IS...a Rota-Baxter Algebra? Notices of the AMS, December 2009, Volume 56 Issue 11