
Robinson-Foulds metric
Encyclopedia
The Robinson–Foulds metric is a way to measure the distance between unrooted phylogenetic trees. It is defined as (A + B) where A is the number of partitions of data implied by the first tree but not the second tree and B is the number of partitions of data implied by the second tree but not the first tree.
 , which contracts an edge (combining the nodes, creating a union of their sets). This is analogous to contraction of Bourque. Conversely,
, which contracts an edge (combining the nodes, creating a union of their sets). This is analogous to contraction of Bourque. Conversely, 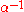 expands an edge (decontraction), where the set can be split in any fashion. The
expands an edge (decontraction), where the set can be split in any fashion. The  function removes all edges from
function removes all edges from 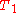 that are not in
that are not in 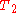 , creating
, creating  , and then
, and then 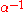 is used to create edges in
is used to create edges in  to build
to build 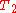 . The number of operations in each of these procedures is equivalent to the number of edges in
. The number of operations in each of these procedures is equivalent to the number of edges in 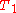 that are not in
that are not in 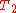 , plus the number of edges in
, plus the number of edges in 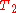 that are not in
that are not in 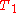 . Each result in
. Each result in  , so the sum of the number of operations is equivalent to a transformation from
, so the sum of the number of operations is equivalent to a transformation from 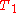 to
to 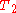 , or vice versa.
, or vice versa.
.
, the metric is often used to compute a distance between two trees. The treedist program in the PHYLIP
suite offers this function, as does the RAxML_standard package.
The Robinson-Foulds metric has also been used in quantitative comparative linguistics to compute distances between trees that represent how languages are related to each other.
Explanation
Given an unrooted tree of nodes and a set of labels (taxa) for each node that could be empty. Only nodes with degree greater than or equal to three can be labeled by an empty set. They define two trees to be the same if they are isomorphic, and this isomorphism preserves the labeling. The construction of the proof is based on a function called , which contracts an edge (combining the nodes, creating a union of their sets). This is analogous to contraction of Bourque. Conversely,
, which contracts an edge (combining the nodes, creating a union of their sets). This is analogous to contraction of Bourque. Conversely, 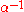 expands an edge (decontraction), where the set can be split in any fashion. The
expands an edge (decontraction), where the set can be split in any fashion. The  function removes all edges from
function removes all edges from 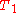 that are not in
that are not in 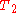 , creating
, creating  , and then
, and then 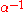 is used to create edges in
is used to create edges in  to build
to build 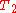 . The number of operations in each of these procedures is equivalent to the number of edges in
. The number of operations in each of these procedures is equivalent to the number of edges in 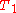 that are not in
that are not in 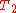 , plus the number of edges in
, plus the number of edges in 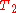 that are not in
that are not in 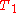 . Each result in
. Each result in  , so the sum of the number of operations is equivalent to a transformation from
, so the sum of the number of operations is equivalent to a transformation from 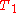 to
to 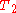 , or vice versa.
, or vice versa.Properties
In their 1981 paper Robinson and Foulds proved that the distance is in fact a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
.
Algorithms for computing the metric
In 1985 Day gave an algorithm based on perfect hashing that computes this distance that has only a linear complexity in the number of nodes in the trees. A randomized algorithm that uses hash tables that are not necessarily perfect has been shown to approximate the Robinson-Foulds distance with a bounded error in sublinear time.Specific applications
In phylogeneticsPhylogenetics
In biology, phylogenetics is the study of evolutionary relatedness among groups of organisms , which is discovered through molecular sequencing data and morphological data matrices...
, the metric is often used to compute a distance between two trees. The treedist program in the PHYLIP
PHYLIP
PHYLIP is a free computational phylogenetics package of programs for inferring evolutionary trees . The name is an acronym for PHYLogeny Inference Package. It consists of 35 portable programs, i.e...
suite offers this function, as does the RAxML_standard package.
The Robinson-Foulds metric has also been used in quantitative comparative linguistics to compute distances between trees that represent how languages are related to each other.
Further reading
- D. R. Robinson and L. R. Foulds, "Comparison of phylogenetic trees", Mathematical Biosciences, 1981, volume 53, pages 131-147. http://dx.doi.org/10.1016/0025-5564(81)90043-2
- William H. E. Day, "Optimal algorithms for comparing trees with labeled leaves", Journal of Classification, Number 1, December 1985. http://www.springerlink.com/content/q5906x80g44p44k8/
- Nicholas D. Pattengale, Eric J. Gottlieb, Bernard M.E. Moret, "Efficiently Computing the Robinson–Foulds Metric", Journal of Computational Biology, July 2007, 14(6): 724-735. doi:10.1089/cmb.2007.R012. http://www.liebertonline.com/doi/abs/10.1089/cmb.2007.R012

