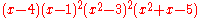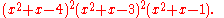In the mathematical

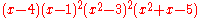
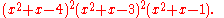
Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

 field of graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

, the Robertson graph or (4,5)-cage is a 4-regular

Regular graph

In graph theory, a regular graph is a graph where each vertex has the same number of neighbors; i.e. every vertex has the same degree or valency. A regular directed graph must also satisfy the stronger condition that the indegree and outdegree of each vertex are equal to each other...

 undirected graph with 19 vertices and 38 edges named after Neil Robertson

Neil Robertson (mathematician)

G. Neil Robertson is a mathematician working mainly in topological graph theory, currently a distinguished professor at the Ohio State University. He earned his Ph.D. in 1969 at the University of Waterloo under his doctoral advisor William Tutte. According to the criteria of the Erdős Number...

.

The Robertson graph is the unique (4,5)-cage graph and was discovered by Robertson in 1964. As a cage graph, it is the smallest 4-regular graph with girth 5.

It has chromatic number 3, chromatic index 5, diameter 3, radius 3 and is both 4-vertex-connected

K-vertex-connected graph

In graph theory, a graph G with vertex set V is said to be k-vertex-connected if the graph remains connected when you delete fewer than k vertices from the graph...

 and 4-edge-connected

K-edge-connected graph

In graph theory, a graph is k-edge-connected if it remains connected whenever fewer than k edges are removed.-Formal definition:Let G =  be an arbitrary graph....

.

The Robertson graph is also a Hamiltonian graph which possesses distinct directed Hamiltonian cycles.

Algebraic properties

The Robertson graph is not a vertex-transitive graph

Vertex-transitive graph

In the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...

 and its full automorphism group is isomorphic to the dihedral group

Dihedral group

In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...

 of order 24, the group of symmetries of an regular dodecagon

Dodecagon

In geometry, a dodecagon is any polygon with twelve sides and twelve angles.- Regular dodecagon :It usually refers to a regular dodecagon, having all sides of equal length and all angles equal to 150°...

, including both rotations and reflections.

The characteristic polynomial

Characteristic polynomial

In linear algebra, one associates a polynomial to every square matrix: its characteristic polynomial. This polynomial encodes several important properties of the matrix, most notably its eigenvalues, its determinant and its trace....

of the Robertson graph is