
Rice-Shapiro theorem
Encyclopedia
In computability theory
, the Rice–Shapiro theorem is a generalization of Rice's theorem
, and is named after Henry Gordon Rice
and Norman Shapiro
.
on the domain of natural numbers such that the set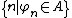 is recursively enumerable, where
is recursively enumerable, where  denotes the
denotes the  -th partial-recursive function in a Gödel number
-th partial-recursive function in a Gödel number
ing.
Then for any unary partial-recursive function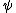 , we have:
, we have:
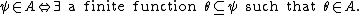
In the given statement, a finite function is a function with a finite domain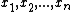 and
and 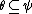 means that for every
means that for every  it holds that
it holds that 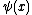 is defined and equal to
is defined and equal to 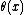 .
.
In general, one can obtain the following statement: The set is recursively enumerable iff the following two conditions hold:
is recursively enumerable iff the following two conditions hold:
(a)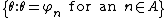 is recursively enumerable;
is recursively enumerable;
(b)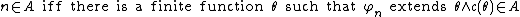 where
where 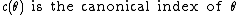 .
.
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, the Rice–Shapiro theorem is a generalization of Rice's theorem
Rice's theorem
In computability theory, Rice's theorem states that, for any non-trivial property of partial functions, there is no general and effective method to decide whether an algorithm computes a partial function with that property...
, and is named after Henry Gordon Rice
Henry Gordon Rice
Henry Gordon Rice is a logician and mathematician best known as the author of Rice's theorem, which he proved in his doctoral dissertation of 1951 at Syracuse University. He was also a Professor of Mathematics at the University of New Hampshire. After 1960 he was employed by Computer Sciences...
and Norman Shapiro
Norman Shapiro
Norman Z. Shapiro is an American mathematician,who is the co-author of the Rice–Shapiro theorem.Shapiro spent the summer of 1954 at Bell Laboratories in Murray Hill, New Jerseywhere, in collaboration withKarel de Leeuw,Ed Moore, and...
.
Informal statement
The statement can be expressed informally as follows: given that a computable function (viewed as a black-box) is an infinite object, and we cannot hope to develop a general algorithm studying a property of function on infinite input-output pairs; there is in general no truly better way than to apply the function on some inputs and hope to get their outputs.Formal statement
Let A be a set of partial-recursive unary functionsFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
on the domain of natural numbers such that the set
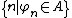 is recursively enumerable, where
is recursively enumerable, where  denotes the
denotes the  -th partial-recursive function in a Gödel number
-th partial-recursive function in a Gödel numberGödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
ing.
Then for any unary partial-recursive function
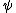 , we have:
, we have: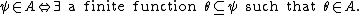
In the given statement, a finite function is a function with a finite domain
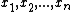 and
and 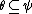 means that for every
means that for every  it holds that
it holds that 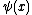 is defined and equal to
is defined and equal to 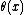 .
.In general, one can obtain the following statement: The set
 is recursively enumerable iff the following two conditions hold:
is recursively enumerable iff the following two conditions hold:(a)
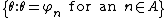 is recursively enumerable;
is recursively enumerable;(b)
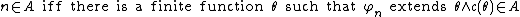 where
where 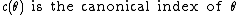 .
.

