
Rice's theorem
Encyclopedia
In computability theory
, Rice's theorem states that, for any non-trivial property of partial functions, there is no general and effective method to decide
whether an algorithm
computes a partial function with that property. Here, a property of partial functions is called trivial if it holds for all partial computable functions or for none, and an effective decision method is called general if it decides correctly for every algorithm.
The theorem is named after Henry Gordon Rice
, and is also known as the Rice-Myhill-Shapiro theorem after Rice, John Myhill
, and Norman Shapiro
.
follows.
Let S be a set of languages
that is nontrivial, meaning
Then, it is undecidable
to determine whether the language decided by an arbitrary Turing machine
lies in S.
In practice, this means that there is no machine that can always decide whether the language of a given Turing machine has a particular nontrivial property. Special cases include the undecidability of whether a Turing machine accepts a particular string, whether a Turing machine recognizes a particular recognizable language, and whether the language recognized by a Turing machine could be recognized by a nontrivial simpler machine, such as a finite automaton
.
It is important to note that Rice's theorem does not say anything about those properties of machines or programs which are not also properties of functions and languages. For example, whether a machine runs for more than 100 steps on some input is a decidable property, even though it is non-trivial. Implementing exactly the same language, two different machines might require a different number of steps to recognize the same input. Similarly, whether a machine has more than 5 states is a decidable property. Where a property is of the kind that either of the two machines may or may not have it, while still implementing exactly the same language, the property is of the machines and not of the language, and Rice's Theorem does not apply.
Using Rogers
' characterization of acceptable programming systems, Rice's Theorem may essentially be generalized from Turing machines to most computer programming language
s: there exists no automatic method that decides with generality non-trivial questions on the black-box behavior of computer programs.
As an example, consider the following variant of the halting problem
: Take the property a partial function F has if F
is defined for argument 1. It is obviously non-trivial, since there are partial functions that are defined for 1 and others that are
undefined at 1. The 1-halting problem is the problem of deciding of any algorithm whether it defines a function with this property,
i.e., whether the algorithm halts on input 1. By Rice's theorem, the 1-halting problem is undecidable.
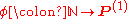 be a Gödel number
be a Gödel number
ing of the computable function
s; a map from the natural numbers to the class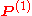 of unary (partial) computable functions.
of unary (partial) computable functions.
Denote by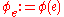 the
the  th (partial) computable function.
th (partial) computable function.
We identify each property that a computable function may have with the subset of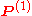 consisting of the functions with that property.
consisting of the functions with that property.
Thus given a set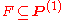 , a computable function
, a computable function 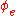 has property F if and only if
has property F if and only if 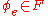 . For each property
. For each property 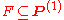 there is an associated decision problem
there is an associated decision problem
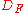 of determining, given e , whether
of determining, given e , whether 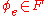 .
.
Rice's theorem states that the decision problem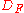 is decidable
is decidable
(also called recursive or computable) if and only if or
or 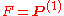 .
.
states that for every Gödel number
ing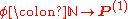 of the computable function
of the computable function
s and every computable function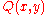 , there is an index
, there is an index  such that
such that 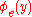 returns
returns 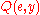 . (In the following, we will say that
. (In the following, we will say that 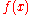 "returns"
"returns" 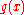 if either
if either  , or both
, or both 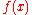 and
and 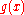 are undefined.) Intuitively,
are undefined.) Intuitively, 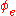 is a quine, a function that returns its own source code (Gödel number), except that rather than returning it directly,
is a quine, a function that returns its own source code (Gödel number), except that rather than returning it directly, 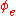 passes its Gödel number to
passes its Gödel number to  and returns the result.
and returns the result.
Let be a set of computable functions such that
be a set of computable functions such that 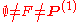 . Then there are computable functions
. Then there are computable functions 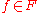 and
and 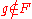 . Suppose that the set of indices
. Suppose that the set of indices  such that
such that 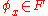 is decidable; then, there exists a function
is decidable; then, there exists a function 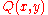 that returns
that returns 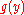 if
if 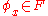 ,
,  otherwise. By the corollary to the recursion theorem, there is an index
otherwise. By the corollary to the recursion theorem, there is an index  such that
such that 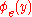 returns
returns 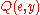 . But then, if
. But then, if 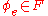 , then
, then 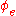 is the same function as
is the same function as 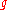 , and therefore
, and therefore 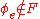 ; and if
; and if 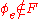 , then
, then 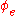 is
is  , and therefore
, and therefore 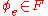 . In both cases, we have a contradiction.
. In both cases, we have a contradiction.
The claim is that we can convert our algorithm for identifying squaring programs into one which identifies functions that halt. We will describe an algorithm which takes inputs a and i and determines whether program a halts when given input i.
The algorithm is simple: we construct a new program t which (1) temporarily ignores its input while it tries to
execute program a on input i, and then, if that halts, (2) returns the square of its input. Clearly, t is a function for computing squares if and only if step (1) halts. Since we've assumed that we can infallibly identify program for computing squares, we can determine whether t is such a program, and therefore whether program a halts on input i. Note that we needn't actually execute t; we need only decide whether it is a squaring program, and, by hypothesis, we know how to do this.
t(n) {
a(i)
return n×n
}
This method doesn't depend specifically on being able to recognize functions that compute squares; as long as some program can do what we're trying to recognize, we can add a call to a to obtain our t. We could have had a method for recognizing programs for computing square roots, or programs for computing the monthly payroll, or programs that halt when given the input "Abraxas", or programs that commit array bounds errors; in each case, we would be able to solve the halting problem similarly.
 For the formal proof, algorithms are presumed to define partial functions over strings
For the formal proof, algorithms are presumed to define partial functions over strings
and are themselves represented by strings. The partial function computed by the algorithm represented by a string a is denoted Fa. This proof proceeds by reductio ad absurdum
: we assume that there is a non-trivial property that is decided by an algorithm, and then show that it follows that we can decide the halting problem
, which is not possible, and therefore a contradiction.
Let us now assume that P(a) is an algorithm that decides some non-trivial property of Fa. Without loss of
generality we may assume that P(no-halt) = "no", with no-halt being the representation of an algorithm that never halts. If this is not true, then this will hold for the negation of the property. Since P decides a non-trivial property, it follows that there is a string b that represents an algorithm and P(b) = "yes". We can then define an algorithm H(a, i) as follows:
We can now show that H decides the halting problem:
Since the halting problem is known to be undecidable, this is a contradiction and the assumption that there is an algorithm P(a) that decides a non-trivial property for the function represented by a must be false.
where is the set of natural numbers, including zero.
is the set of natural numbers, including zero.
whether it has a certain nontrivial property.
In this section, we give an analogue of Rice's theorem for recursive sets, instead of recursively enumerable sets.
Roughly speaking, the analogue says that if one can effectively determine for any recursive set whether it has a certain property,
then finitely many integers determine whether a recursive set has the property.
This result is analogous to the original Rice's theorem because both assert that a property is "decidable"
only if one can determine whether a set has that property by examining for at most finitely many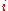
(for no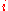 , for the original theorem), if
, for the original theorem), if 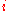 belongs to the set.
belongs to the set.
Let be a class (called a simple game and thought of as a property) of recursive sets.
be a class (called a simple game and thought of as a property) of recursive sets.
If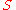 is a recursive set, then for some
is a recursive set, then for some  , computable function
, computable function 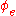
is the characteristic function of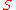 . We call
. We call  a characteristic index for
a characteristic index for 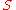 .
.
(There are infinitely many such .)
.)
Let's say the class is computable if there is an algorithm (computable function) that decides
is computable if there is an algorithm (computable function) that decides
for any nonnegative integer (not necessarily a characteristic index),
(not necessarily a characteristic index),
A set extends a string
extends a string  of 0's and 1's
of 0's and 1's
if for any (the length of
(the length of  ),
),
the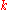 th element of
th element of  is 1 if
is 1 if 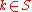 ; is 0 otherwise.
; is 0 otherwise.
For example,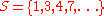 extends string
extends string  .
.
A string is winning determining if any recursive set extending
is winning determining if any recursive set extending  belongs to
belongs to  .
.
A string is losing determining if no recursive set extending
is losing determining if no recursive set extending  belongs to
belongs to  .
.
We can now state the following analogue of Rice's theorem
(Kreisel, Lacombe, and Shoenfield, 1959,
Kumabe and Mihara, 2008):
A class of recursive sets is computable
of recursive sets is computable
if and only if there are a recursively enumerable set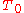 of losing determining strings
of losing determining strings
and a recursively enumerable set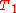 of winning determining strings such that
of winning determining strings such that
any recursive set extends a string in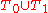 .
.
This result has been applied to foundational problems in computational social choice (more broadly, algorithmic game theory
).
For instance, Kumabe and Mihara (2008, 2008)
apply this result to an investigation of the Nakamura number
s for simple games in cooperative game theory
and social choice theory
.
Computability theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, Rice's theorem states that, for any non-trivial property of partial functions, there is no general and effective method to decide
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
whether an algorithm
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
computes a partial function with that property. Here, a property of partial functions is called trivial if it holds for all partial computable functions or for none, and an effective decision method is called general if it decides correctly for every algorithm.
The theorem is named after Henry Gordon Rice
Henry Gordon Rice
Henry Gordon Rice is a logician and mathematician best known as the author of Rice's theorem, which he proved in his doctoral dissertation of 1951 at Syracuse University. He was also a Professor of Mathematics at the University of New Hampshire. After 1960 he was employed by Computer Sciences...
, and is also known as the Rice-Myhill-Shapiro theorem after Rice, John Myhill
John Myhill
John R. Myhill was a mathematician, born in 1923. He received his Ph.D. from Harvard University under Willard Van Orman Quine in 1949. He was professor at SUNY Buffalo from 1966 until his death in 1987...
, and Norman Shapiro
Norman Shapiro
Norman Z. Shapiro is an American mathematician,who is the co-author of the Rice–Shapiro theorem.Shapiro spent the summer of 1954 at Bell Laboratories in Murray Hill, New Jerseywhere, in collaboration withKarel de Leeuw,Ed Moore, and...
.
Introduction
Another way of stating Rice's theorem that is more useful in computability theoryComputability theory (computer science)
Computability is the ability to solve a problem in an effective manner. It is a key topic of the field of computability theory within mathematical logic and the theory of computation within computer science...
follows.
Let S be a set of languages
Formal language
A formal language is a set of words—that is, finite strings of letters, symbols, or tokens that are defined in the language. The set from which these letters are taken is the alphabet over which the language is defined. A formal language is often defined by means of a formal grammar...
that is nontrivial, meaning
- there exists a Turing machine that recognizes a language in S
- there exists a Turing machine that recognizes a language not in S
Then, it is undecidable
Decision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
to determine whether the language decided by an arbitrary Turing machine
Turing machine
A Turing machine is a theoretical device that manipulates symbols on a strip of tape according to a table of rules. Despite its simplicity, a Turing machine can be adapted to simulate the logic of any computer algorithm, and is particularly useful in explaining the functions of a CPU inside a...
lies in S.
In practice, this means that there is no machine that can always decide whether the language of a given Turing machine has a particular nontrivial property. Special cases include the undecidability of whether a Turing machine accepts a particular string, whether a Turing machine recognizes a particular recognizable language, and whether the language recognized by a Turing machine could be recognized by a nontrivial simpler machine, such as a finite automaton
Finite state machine
A finite-state machine or finite-state automaton , or simply a state machine, is a mathematical model used to design computer programs and digital logic circuits. It is conceived as an abstract machine that can be in one of a finite number of states...
.
It is important to note that Rice's theorem does not say anything about those properties of machines or programs which are not also properties of functions and languages. For example, whether a machine runs for more than 100 steps on some input is a decidable property, even though it is non-trivial. Implementing exactly the same language, two different machines might require a different number of steps to recognize the same input. Similarly, whether a machine has more than 5 states is a decidable property. Where a property is of the kind that either of the two machines may or may not have it, while still implementing exactly the same language, the property is of the machines and not of the language, and Rice's Theorem does not apply.
Using Rogers
Hartley Rogers, Jr
Hartley Rogers, Jr. is a mathematician who has worked in recursion theory, and who is currently a professor in the Mathematics Department of the Massachusetts Institute of Technology. The Rogers equivalence theorem is named after him....
' characterization of acceptable programming systems, Rice's Theorem may essentially be generalized from Turing machines to most computer programming language
Programming language
A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....
s: there exists no automatic method that decides with generality non-trivial questions on the black-box behavior of computer programs.
As an example, consider the following variant of the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
: Take the property a partial function F has if F
is defined for argument 1. It is obviously non-trivial, since there are partial functions that are defined for 1 and others that are
undefined at 1. The 1-halting problem is the problem of deciding of any algorithm whether it defines a function with this property,
i.e., whether the algorithm halts on input 1. By Rice's theorem, the 1-halting problem is undecidable.
Formal statement
Let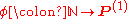 be a Gödel number
be a Gödel numberGödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
ing of the computable function
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s; a map from the natural numbers to the class
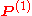 of unary (partial) computable functions.
of unary (partial) computable functions.Denote by
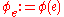 the
the  th (partial) computable function.
th (partial) computable function.We identify each property that a computable function may have with the subset of
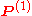 consisting of the functions with that property.
consisting of the functions with that property.Thus given a set
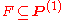 , a computable function
, a computable function 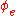 has property F if and only if
has property F if and only if 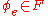 . For each property
. For each property 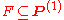 there is an associated decision problem
there is an associated decision problemDecision problem
In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...
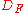 of determining, given e , whether
of determining, given e , whether 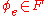 .
.Rice's theorem states that the decision problem
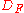 is decidable
is decidableRecursive set
In computability theory, a set of natural numbers is called recursive, computable or decidable if there is an algorithm which terminates after a finite amount of time and correctly decides whether or not a given number belongs to the set....
(also called recursive or computable) if and only if
 or
or 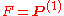 .
.Examples
According to Rice's theorem, if there is at least one computable function in a particular class C of computable functions and another computable function not in C then the problem of deciding whether a particular program computes a function in C is undecidable. For example, Rice's theorem shows that each of the following sets of computable functions is undecidable:- The class of computable functions that return 0 for every input, and its complement.
- The class of computable functions that return 0 for at least one input, and its complement.
- The class of computable functions that are constant, and its complement.
Proof by Kleene's recursion theorem
A corollary to Kleene's recursion theoremKleene's recursion theorem
In computability theory, Kleene's recursion theorems are a pair of fundamental results about the application of computable functions to their own descriptions...
states that for every Gödel number
Gödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
ing
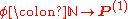 of the computable function
of the computable functionComputable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
s and every computable function
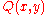 , there is an index
, there is an index  such that
such that 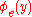 returns
returns 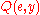 . (In the following, we will say that
. (In the following, we will say that 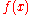 "returns"
"returns" 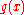 if either
if either  , or both
, or both 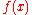 and
and 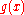 are undefined.) Intuitively,
are undefined.) Intuitively, 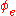 is a quine, a function that returns its own source code (Gödel number), except that rather than returning it directly,
is a quine, a function that returns its own source code (Gödel number), except that rather than returning it directly, 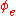 passes its Gödel number to
passes its Gödel number to  and returns the result.
and returns the result.Let
 be a set of computable functions such that
be a set of computable functions such that 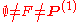 . Then there are computable functions
. Then there are computable functions 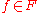 and
and 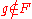 . Suppose that the set of indices
. Suppose that the set of indices  such that
such that 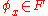 is decidable; then, there exists a function
is decidable; then, there exists a function 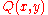 that returns
that returns 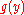 if
if 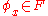 ,
,  otherwise. By the corollary to the recursion theorem, there is an index
otherwise. By the corollary to the recursion theorem, there is an index  such that
such that 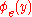 returns
returns 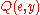 . But then, if
. But then, if 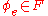 , then
, then 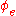 is the same function as
is the same function as 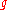 , and therefore
, and therefore 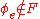 ; and if
; and if 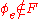 , then
, then 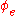 is
is  , and therefore
, and therefore 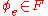 . In both cases, we have a contradiction.
. In both cases, we have a contradiction.Proof sketch
Suppose, for concreteness, that we have an algorithm for examining a program p and determining infallibly whether p is an implementation of the squaring function, which takes an integer d and returns d2. The proof works just as well if we have an algorithm for deciding any other nontrivial property of programs, and will be given in general below.The claim is that we can convert our algorithm for identifying squaring programs into one which identifies functions that halt. We will describe an algorithm which takes inputs a and i and determines whether program a halts when given input i.
The algorithm is simple: we construct a new program t which (1) temporarily ignores its input while it tries to
execute program a on input i, and then, if that halts, (2) returns the square of its input. Clearly, t is a function for computing squares if and only if step (1) halts. Since we've assumed that we can infallibly identify program for computing squares, we can determine whether t is such a program, and therefore whether program a halts on input i. Note that we needn't actually execute t; we need only decide whether it is a squaring program, and, by hypothesis, we know how to do this.
t(n) {
a(i)
return n×n
}
This method doesn't depend specifically on being able to recognize functions that compute squares; as long as some program can do what we're trying to recognize, we can add a call to a to obtain our t. We could have had a method for recognizing programs for computing square roots, or programs for computing the monthly payroll, or programs that halt when given the input "Abraxas", or programs that commit array bounds errors; in each case, we would be able to solve the halting problem similarly.
Formal proof

String (computer science)
In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....
and are themselves represented by strings. The partial function computed by the algorithm represented by a string a is denoted Fa. This proof proceeds by reductio ad absurdum
Reductio ad absurdum
In logic, proof by contradiction is a form of proof that establishes the truth or validity of a proposition by showing that the proposition's being false would imply a contradiction...
: we assume that there is a non-trivial property that is decided by an algorithm, and then show that it follows that we can decide the halting problem
Halting problem
In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
, which is not possible, and therefore a contradiction.
Let us now assume that P(a) is an algorithm that decides some non-trivial property of Fa. Without loss of
generality we may assume that P(no-halt) = "no", with no-halt being the representation of an algorithm that never halts. If this is not true, then this will hold for the negation of the property. Since P decides a non-trivial property, it follows that there is a string b that represents an algorithm and P(b) = "yes". We can then define an algorithm H(a, i) as follows:
- 1. construct a string t that represents an algorithm T(j) such that
- T first simulates the computation of Fa(i)
- then T simulates the computation of Fb(j) and returns its result.
- 2. return P(t).
We can now show that H decides the halting problem:
- Assume that the algorithm represented by a halts on input i. In this case Ft = Fb and, because P(b) = "yes" and the output of P(x) depends only on Fx, it follows that P(t) = "yes" and, therefore H(a, i) = "yes".
- Assume that the algorithm represented by a does not halt on input i. In this case Ft = Fno-halt, i.e., the partial function that is never defined. Since P(no-halt) = "no" and the output of P(x) depends only on Fx, it follows that P(t) = "no" and, therefore H(a, i) = "no".
Since the halting problem is known to be undecidable, this is a contradiction and the assumption that there is an algorithm P(a) that decides a non-trivial property for the function represented by a must be false.
Rice's theorem and index sets
Rice's theorem can be succinctly stated in terms of index sets:Let
 be a class of partial recursive functions with index setIndex set (recursion theory)In the field of recursion theory, index sets describe classes of partial recursive functions, specifically they give all indices of functions in that class according to a fixed enumeration of partial recursive functions .-Definition:...
be a class of partial recursive functions with index setIndex set (recursion theory)In the field of recursion theory, index sets describe classes of partial recursive functions, specifically they give all indices of functions in that class according to a fixed enumeration of partial recursive functions .-Definition:...
 . Then
. Then  is recursive if and only if
is recursive if and only if  or
or  .
.
where
 is the set of natural numbers, including zero.
is the set of natural numbers, including zero.An analogue of Rice's theorem for recursive sets
One can regard Rice's theorem as asserting the impossibility of effectively deciding for any recursively enumerable setwhether it has a certain nontrivial property.
In this section, we give an analogue of Rice's theorem for recursive sets, instead of recursively enumerable sets.
Roughly speaking, the analogue says that if one can effectively determine for any recursive set whether it has a certain property,
then finitely many integers determine whether a recursive set has the property.
This result is analogous to the original Rice's theorem because both assert that a property is "decidable"
only if one can determine whether a set has that property by examining for at most finitely many
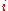
(for no
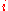 , for the original theorem), if
, for the original theorem), if 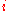 belongs to the set.
belongs to the set.Let
 be a class (called a simple game and thought of as a property) of recursive sets.
be a class (called a simple game and thought of as a property) of recursive sets.If
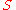 is a recursive set, then for some
is a recursive set, then for some  , computable function
, computable function 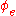
is the characteristic function of
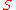 . We call
. We call  a characteristic index for
a characteristic index for 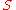 .
.(There are infinitely many such
 .)
.)Let's say the class
 is computable if there is an algorithm (computable function) that decides
is computable if there is an algorithm (computable function) that decidesfor any nonnegative integer
 (not necessarily a characteristic index),
(not necessarily a characteristic index),
- if
 is a characteristic index for a recursive set belonging to
is a characteristic index for a recursive set belonging to  , then the algorithm gives "yes";
, then the algorithm gives "yes"; - if
 is a characteristic index for a recursive set not belonging to
is a characteristic index for a recursive set not belonging to  , then the algorithm gives "no".
, then the algorithm gives "no".
A set
 extends a string
extends a string  of 0's and 1's
of 0's and 1'sif for any
 (the length of
(the length of  ),
),the
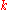 th element of
th element of  is 1 if
is 1 if 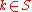 ; is 0 otherwise.
; is 0 otherwise.For example,
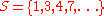 extends string
extends string  .
.A string
 is winning determining if any recursive set extending
is winning determining if any recursive set extending  belongs to
belongs to  .
.A string
 is losing determining if no recursive set extending
is losing determining if no recursive set extending  belongs to
belongs to  .
.We can now state the following analogue of Rice's theorem
(Kreisel, Lacombe, and Shoenfield, 1959,
Kumabe and Mihara, 2008):
A class
 of recursive sets is computable
of recursive sets is computableif and only if there are a recursively enumerable set
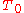 of losing determining strings
of losing determining stringsand a recursively enumerable set
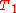 of winning determining strings such that
of winning determining strings such thatany recursive set extends a string in
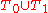 .
.This result has been applied to foundational problems in computational social choice (more broadly, algorithmic game theory
Algorithmic game theory
Algorithmic game theory is an area in the intersection of game theory and algorithm design, whose objective is to design algorithms in strategic environments. Typically, in Algorithmic Game Theory problems, the input to a given algorithm is distributed among many players who have a personal...
).
For instance, Kumabe and Mihara (2008, 2008)
apply this result to an investigation of the Nakamura number
Nakamura number
In cooperative game theory and social choice theory, the Nakamura number measures the degree of rationalityof preference aggregation rules , such as voting rules....
s for simple games in cooperative game theory
Cooperative game
In game theory, a cooperative game is a game where groups of players may enforce cooperative behaviour, hence the game is a competition between coalitions of players, rather than between individual players...
and social choice theory
Social choice theory
Social choice theory is a theoretical framework for measuring individual interests, values, or welfares as an aggregate towards collective decision. A non-theoretical example of a collective decision is passing a set of laws under a constitution. Social choice theory dates from Condorcet's...
.
See also
- Gödel's incompleteness theoremsGödel's incompleteness theoremsGödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...
- Halting ProblemHalting problemIn computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...
- Rice-Shapiro theoremRice-Shapiro theoremIn computability theory, the Rice–Shapiro theorem is a generalization of Rice's theorem, and is named after Henry Gordon Rice and Norman Shapiro.-Informal statement:...
- Recursion theoryRecursion theoryComputability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...

