
Index set (recursion theory)
Encyclopedia
In the field of recursion theory
, index sets describe classes of partial recursive functions, specifically they give all indices of functions in that class according to a fixed enumeration of partial recursive functions (a Gödel number
ing).
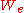 and the eth such function (whose domain is
and the eth such function (whose domain is 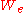 ) is
) is 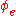 .
.
Let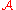 be a class of partial recursive functions. If
be a class of partial recursive functions. If 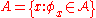 then
then  is the index set of
is the index set of 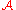 . In general
. In general  is an index set if for every
is an index set if for every 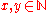 with
with  (i.e. they index the same function), we have
(i.e. they index the same function), we have  . Intuitively, these are the sets of natural numbers that we describe only with reference to the functions they index.
. Intuitively, these are the sets of natural numbers that we describe only with reference to the functions they index.
Index sets and Rice's theorem
Most index sets are incomputable (non-recursive) aside from two trivial exceptions. This is stated in Rice's theorem:
where is the set of natural numbers, including zero.
is the set of natural numbers, including zero.
Rice's theorem says "any nontrivial property of partial recursive functions is undecidable"
Recursion theory
Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...
, index sets describe classes of partial recursive functions, specifically they give all indices of functions in that class according to a fixed enumeration of partial recursive functions (a Gödel number
Gödel number
In mathematical logic, a Gödel numbering is a function that assigns to each symbol and well-formed formula of some formal language a unique natural number, called its Gödel number. The concept was famously used by Kurt Gödel for the proof of his incompleteness theorems...
ing).
Definition
Fix an enumeration of all partial recursive functions, or equivalently of recursively enumerable sets whereby the eth such set is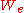 and the eth such function (whose domain is
and the eth such function (whose domain is 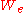 ) is
) is 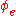 .
.Let
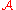 be a class of partial recursive functions. If
be a class of partial recursive functions. If 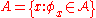 then
then  is the index set of
is the index set of 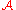 . In general
. In general  is an index set if for every
is an index set if for every 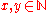 with
with  (i.e. they index the same function), we have
(i.e. they index the same function), we have  . Intuitively, these are the sets of natural numbers that we describe only with reference to the functions they index.
. Intuitively, these are the sets of natural numbers that we describe only with reference to the functions they index.Index sets and Rice's theoremRice's theoremIn computability theory, Rice's theorem states that, for any non-trivial property of partial functions, there is no general and effective method to decide whether an algorithm computes a partial function with that property...
Most index sets are incomputable (non-recursive) aside from two trivial exceptions. This is stated in Rice's theorem:Letbe a class of partial recursive functions with index set
. Then
is recursive if and only if
is empty, or
is all of
.
where
 is the set of natural numbers, including zero.
is the set of natural numbers, including zero.Rice's theorem says "any nontrivial property of partial recursive functions is undecidable"

